🐕

MCMC法のメトロポリス法をやってみよう

2023/04/08に公開

Python

Streamlit

メトロポリス法

tech

本記事の目的

今回はベイズ推定のサンプリング方法の第二弾。第一弾のギブスサンプリングについてはこちらをどうぞ。

今回はメトロポリス法についてまとめていく。

ギブスサンプリングとメトロポリス法の使い分けについて

どちらもMCMC法のサンプリング方法であるが、適した場面が異なる。一般的に言われているのが、ギブスサンプリングは条件付き確率が求めやすい形のとき、メトロポリス法は条件付き確率が求めにくい形のときに用いられるということ。ってことはメトロポリス法の方が汎用性があり、ずっと使い続ければ良いんじゃと思うかもしれないが、メトロポリス法の方がパラメータ調整が難しい（後述）。

理論：メトロポリス法をやってみよう

では、前回と同様にメトロポリス法のサンプリング方法を理論→実践で行う。こちらのサイトを参考にさせていただいた。

まずメトロポリス法もMCMC法の一種なので、直前のデータから次のデータを求めている。ここで一例として正規分布で重みづけした乱数の生成方法について述べる。
メトロポリス法では、確率が大きくなるサンプリングでは必ずデータを更新し、確率が小さくなるサンプリングでは、そのサンプリングを一定確率で棄却する。言葉だけでは全然わからないと思うので、上記のサイトのとても分かりやすい図を使わせてもらう。

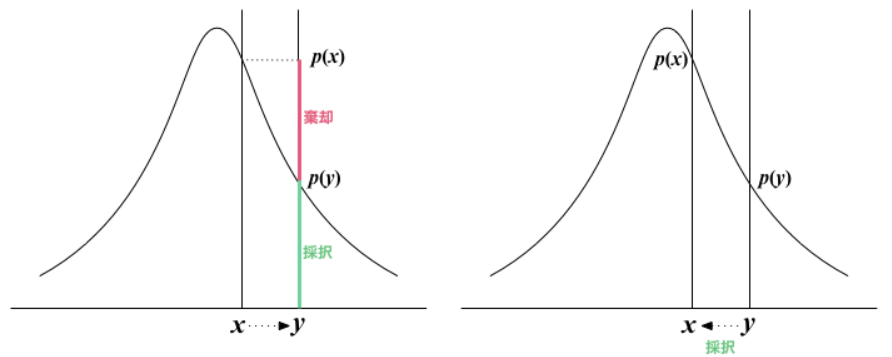
メトロポリス法(https://wagtail.cds.tohoku.ac.jp/coda/python/stochastic-methods/metropolis-method.html)

少し砕けた例を挙げる。確率とは言い換えると居心地の良さである。確率が大きいほど居心地が良いので、今の状態(x)から次の状態(y)に移らなければならないときに、次の状態の方が居心地が良ければ必ず動きたくなりますよね。しかし、次の状態の方が居心地が悪いとき、しぶしぶ次の状態に移るケースもあれば、動かない（今の状態をキープ）と思います。このような考え方がメトロポリス法です。このしぶしぶ動く確率rは $r=\frac{p(y)}{p(x)}$ で表せる。これをフロー図で書くと次の通り。

①初期値 $x_1$ を設定
②初期値の確率 $p(x_1)$ を計算
③乱数 $\epsilon$ を発生（左右対称な分布を持つ乱数ならば何でもよい）
④ $x_2=x_1+\epsilon$
⑤2番目データの確率 $p(x_2)$ を計算
⑥ $r=\frac{p(x_2)}{p(x_1)}$ を計算
⑦-1 $p(x_2)>p(x_1)$ なら $x_2$ を採用
⑦-2 $p(x_2)<p(x_1)$ なら確率rで $x_2$ を採用、確率1-rで $x_2$ を棄却
⑧乱数 $\epsilon$ を発生（左右対称な分布を持つ乱数ならば何でもよい）
⑨ $x_3=x_2(あるいはx_1)+\epsilon$ とどんどんxを更新していく
⑩このxを $w$ 回に1回サンプリングする。
⑪繰り返す

このようにデータを更新し、「時々」サンプリングを行う作業を繰り返す。ギブスサンプリングと異なり、棄却するサンプルも生じるため、ある程度モンテカルロ法の試行回数は多くしないといけないことが感覚的に分かる。

パラメータに注目すると、ギブスサンプリングとは異なり、 $\epsilon$ （ステップ幅）や $w$ （ステップ数=サンプリング間隔）も決める必要がある。これが難しい。ステップ幅やステップ数が小さすぎると同じようなところをサンプリングしたりするため、目的の確率分布と同じようなサンプリング結果に中々ならない。逆にステップ幅やステップ数が大きすぎると精度の悪いサンプリング結果になったりする。下記にプログラムコードを記しているので、是非試してほしい。

実践：メトロポリス法をやってみよう

今回は下記のサイトを参考にさせていただいた。

まずは環境構成とディレクトリ構成図。

環境構成

Python：3.9.13
VSCode：1.76.2

ディレクトリ構成図

METROPOLIS
├ backend.py
└ frontend.py

次に、backend.pyのコード。今回は目標分布（実サンプルから得られた確率分布）を二つ山があるような混合分布にしている。ギブスサンプリングではサンプリングしにくそうな分布であるが、メトロポリス法ではどのようにサンプリングを行っているかに注目しながら書いてみよう。

backend.py

import random
import math
import matplotlib.pyplot as plt
def f(x):
    return 0.2*1/math.sqrt(2*math.pi)*math.exp(-(x-2)**2/2) + 0.7*1/math.sqrt(2*math.pi)*math.exp(-x**2/2) + 0.2*1/math.sqrt(2*math.pi)*math.exp(-(x-5)**2/2)

def metropolis(x_init,iters,step,step_width,burn_in):
    x = x_init
    sdata=[]
    cnt=0
    for _ in range(iters):
        y = x + step*random.uniform(-1,1)
        alpha = min(1, f(y)/f(x))
        r = random.uniform(0,1)
        if r > alpha:
            y = x
        x = y
        cnt += 1
        if cnt%step_width==0:
            sdata.append(x)

    sdata=sdata[burn_in:]

    return sdata

def xy_data(x_min,x_max):
    xdata=[]
    ydata=[]
    x=x_min
    while x<x_max:
        xdata.append(x)
        ydata.append(f(x))
        x +=0.01
    
    return xdata,ydata

def f(x)について
1/math.sqrt(2*math.pi)*math.exp(-(x-2)**2/2)と書いているが、感の良い方はstats.norm.pdf(x,-2,1)を書いた方がスッキリするのではと思っているだろう。私も最初はその書き方で行っていたのだが、計算に時間がかかる。statsを毎回呼び出しているからだろうか。メトロポリス法では試行回数を多くするので、計算に時間がかからない本コードを採用している。

random.uniform(-1,1)について
ここが悩みポイント。色々なサイトを見ているのだが、ここを標準正規分布の乱数を使っている方もいる。左右対称になっていれば、ここの乱数発生は何でも良いらしい。左右対称である理由は増減の確率が同じになるためだろうが、何でも良い理由が分からない。標準正規分布だったら、平均値(0)の値で最も動きやすいのに対し、一様分布だったらどの値でも同じ確率で動くので、結果も異なってくるのではと素人ながらに感じている。もう少し調査する。

次にfrontend.pyのコード。

frontend.py

import streamlit as st
from backend import xy_data,metropolis
import matplotlib.pyplot as plt

with st.form(key="metropolis"):
    x_min:int=st.number_input("xの最小値",-100,100,-5)
    x_max:int=st.number_input("xの最大値",-100,100,10)
    x_init:int=st.number_input("xの初期値",-100,100,0)
    iters:int=st.slider("試行回数",0,1000000,200000,100)
    burn_in:int=st.slider("バーンイン",0,1000000,1000,100)
    step:float=st.slider("ステップ数",0.1,10.0,1.0,0.1)
    step_width:int=st.number_input("ステップ幅",1,100,2)

    st_submit_button=st.form_submit_button("推定")

    if st_submit_button:
        fig1 = plt.figure()
        plt.title("DISTRIBUTION")
        plt.plot(xy_data(x_min,x_max)[0],xy_data(x_min,x_max)[1],label='目標分布')
        plt.hist(metropolis(x_init,iters,step,step_width,burn_in), bins=100, density=True,label='推測データ')
        plt.xlabel('x')
        plt.ylabel('P(x)')
        plt.legend(prop = {'family' : 'MS Gothic'})
        plt.grid(True)
        st.pyplot(fig1)

step:float=st.number_input("ステップ数",0.1,10.0,1.0,step=0.1)について
いつもの数字の入力だが、今回は浮動小数点型を使い、少し躓いた。st.number_input("ステップ数",0.1,10,1,step=0.1)と書いており、下記のエラーが生じていたためだ。

streamlit.errors.StreamlitAPIException: All numerical arguments must be of the same type

今回のコードで書いてある通り、浮動小数点型を使うときは全ての数字を浮動小数点型にしないといけない。

fig1 = plt.figure()について
今まで気付かなかったのだが、Streamlitではfigやaxes(axis)を定義しておいた方が良い。定義していなくても、Streamlit上に図示されるのだが、下記の警告コードが出てしまう。

PyplotGlobalUseWarning: You are calling st.pyplot() without any arguments. After December 1st, 2020, we will remove the ability to do this as it requires the use of Matplotlib's global figure object, which is not thread-safe.

density=Trueについて
plt.hist()の初期設定はデータ個数を表すようになっている。今回は確率なので、引数にdensity=trueを設定している。

plt.legend(prop = {'family' : 'MS Gothic'})について
matplotlibのグラフ内で日本語を使うとき、何も設定しないと文字化けが生じてしまう。そこで、引数propに{'family' : 'MS Gothic'}と書くことで、文字化けを防いでいる。MS Gothic以外にも日本語が使えるフォントが色々あるので、気になる方は調べて。

結果：メトロポリス法をやってみよう

下記の様な初期画面になるだろう。

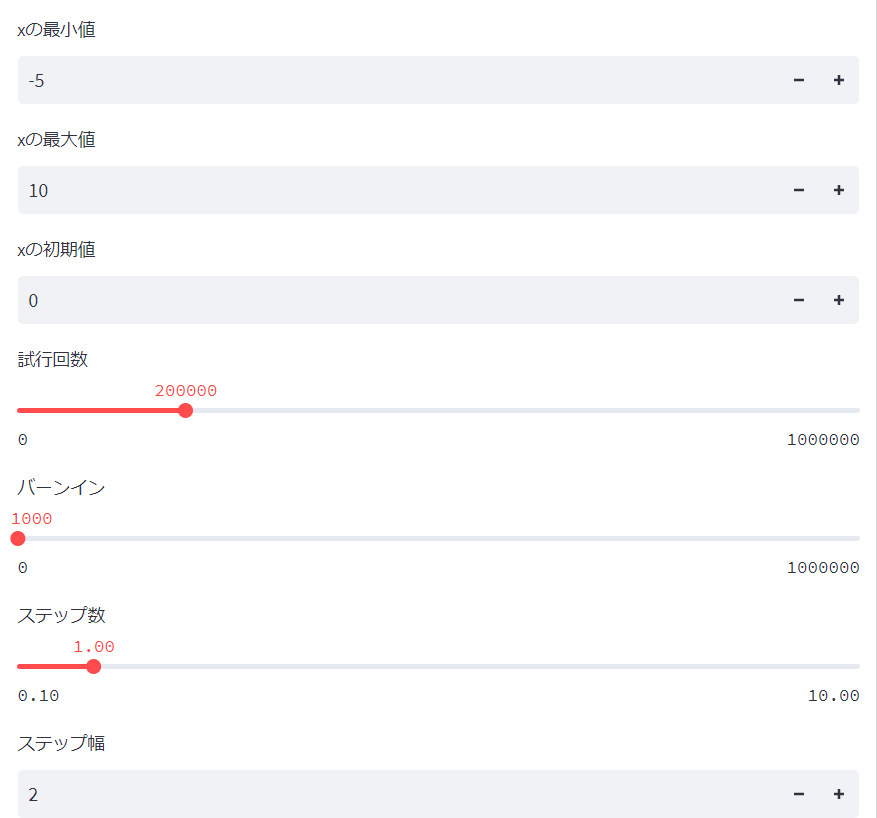
この値のまま実行してみると、下記の様な値になるはず。

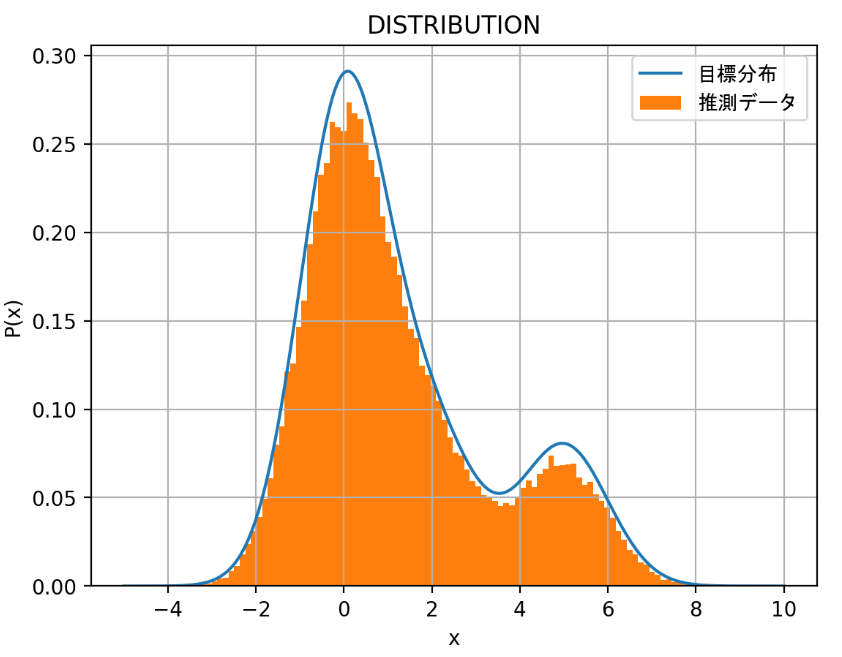
結構、推測データが目標分布に近いのが分かると思う。ただ、近づけるためにステップ数やステップ幅など色々なパラメータを調整している。興味がある方は、ここら辺のパラメータを変えて試してほしい。

まとめ

確かに確率分布が複雑になっても、近しいサンプリング結果になった。しかし、ギブスサンプリングと異なり調整するパラメータが多く、設定が難しい。このように両者ともにメリット・デメリットがあることに注意が必要。（ちなみに両者をまとめて一般化ものをメトロポリス・ヘイスティング法という）お疲れさまでした。