本記事の目的
異常検知の代表的手法であるMT法について自分用のメモを残す。
MT法とは
異常検知手法の代表的な手法である。異常検知には、回帰や決定木、深層学習などの手法でも行えるが、MT法の良いところは「計算速度が速く、説明可能な統計的手法」である。下記のリンクがMT法の特徴を詳しくまとめているので、確認してほしい。
https://www.angletry.com/diffmt/
理論編:MT法を分解して考えてみよう
ステップ0:前準備
シンプルに考えたいので、2変量の装置時系列データを考える。ここでは変量を圧力と水温としておく。時刻1からnまでのデータ組X=(X_1,X_2,…,X_n)は、時刻iでの圧力と水温の観測値をx_i=(x_{i,圧力},x_{i,水温})とすると次のように表せる。
X=
\begin{pmatrix}
x_{1,圧力} & x_{1,水温} \\
\vdots & \vdots \\
x_{n,圧力} & x_{n,水温}
\end{pmatrix}
ステップ1:観測データを標準化する
各変量ごとにスケールが異なるので、まずは観測データを変量ごとに標準化してみよう。標準化には母平均と母分散を推定しなければならないので、まずは時刻nまでの観測値から母平均を推定する。今回の場合だと
\hat{\mu}_{圧力}=\frac{1}{n} \Sigma_{i=1}^{n} x_{i,圧力} \\
\hat{\mu}_{水温}=\frac{1}{n} \Sigma_{i=1}^{n} x_{i,水温}
となる。母平均が推定できたら、次は変量ごとの不偏母分散も計算してみよう。
\hat{\sigma}_{圧力}^2=\frac{1}{n-1} \Sigma_{i=1}^{n} (x_{i,圧力}-\hat{\mu}_{圧力})^2 \\
\hat{\sigma}_{水温}^2=\frac{1}{n-1} \Sigma_{i=1}^{n} (x_{i,水温}-\hat{\mu}_{水温})^2
これらの値から、時刻iの変量ごとの標準化データy_iは次のように表せる。
y_{i,圧力}=\frac{x_{i,圧力}-\hat{\mu}_{圧力}}{\hat{\sigma}_{圧力}} \\
y_{i,水温}=\frac{x_{i,水温}-\hat{\mu}_{水温}}{\hat{\sigma}_{水温}}
ここまでやってきたことを図示すると下記の通りである。
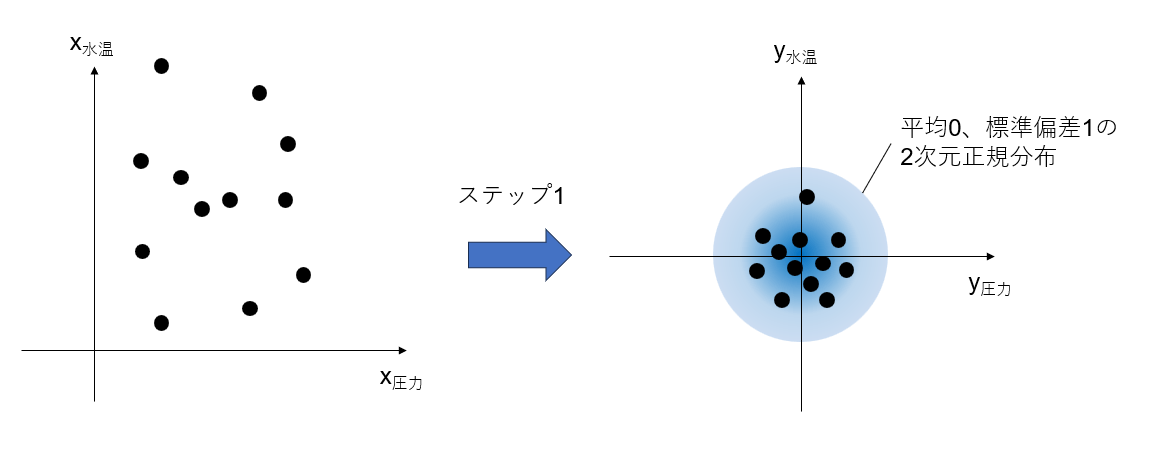
後々使うので、行列で表現しておこう。
\bm{y_i}=(y_{i,圧力},y_{i,水温})=
(x_{i,圧力}-\hat{\mu}_{圧力},x_{i,水温}-\hat{\mu}_{水温})
\begin{pmatrix}
\hat{\sigma}_{圧力}^{-1} & 0 \\
0 & \hat{\sigma}_{水温}^{-1}
\end{pmatrix}
ステップ2:変量間の主成分を求める
次にステップ1の変量ごとの標準化データを用いて、相関行列Rを求める。相関行列とは行と列に対応する変量間の相関係数を表す行列である。変量がaとbだとすると、相関係数=変量aとbの共分散/{変量aの標準偏差×変量bの標準偏差}である。変量aとbの共分散\sigma_{a,b}は、
\begin{align*}
\sigma_{a,b}&=\frac{1}{n-1} \Sigma_{i=1}^{n} (x_{i,a}-\hat{\mu}_{a}) (x_{i,b}-\hat{\mu}_{b})
\\
&=\frac{\hat{\sigma}_{a} \hat{\sigma}_{b}}{n-1} \Sigma_{i=1}^{n} y_{i,a} y_{i,b}
\end{align*}
であり、相関係数r_{a,b}は次のように表せる。
r_{a,b}=\frac{1}{n-1} \Sigma_{i=1}^{n} y_{i,a} y_{i,b}
よって、今回の場合だと相関行列は次のように表せる。
\begin{align*}
R&=
\begin{pmatrix}
r_{圧力,圧力} & r_{圧力,水温} \\
r_{水温,圧力} & r_{水温,水温}
\end{pmatrix}
\\
&=
\frac{1}{n-1}
\begin{pmatrix}
y_{1,圧力} & \cdots & y_{n,圧力} \\
y_{1,水温} & \cdots & y_{n,水温}
\end{pmatrix}
\begin{pmatrix}
y_{1,圧力} & y_{1,水温} \\
\vdots & \vdots \\
y_{n,圧力} & y_{n,水温}
\end{pmatrix}
\end{align*}
相関行列が分かったら固有ベクトルが分かる。第二主成分まで考えるとし、固有値を\lambda_1(>0),\lambda_2(>0)、各主成分方向の固有ベクトルを\bm{u_1}=(u_{1,圧力},u_{1,水温}),\bm{u_2}=(u_{2,圧力},u_{2,水温})とする。数値定義だけでも良いが、後々使うので、以下のように書き下す。なぜこのような式になるかは下記のサイトが分かりやすかったので、気になる方は確認してほしい。
http://racco.mikeneko.jp/Kougi/08s/AS/AS07pr.pdf
\begin{align*}
R
\begin{pmatrix}
u_{1,圧力} & u_{2,圧力} \\
u_{1,水温} & u_{2,水温}
\end{pmatrix}
&=
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{pmatrix}
\begin{pmatrix}
u_{1,圧力} & u_{2,圧力} \\
u_{1,水温} & u_{2,水温}
\end{pmatrix}
\\
\end{align*}
U=\begin{pmatrix} u_{1,圧力} & u_{2,圧力} \\ u_{1,水温} & u_{2,水温} \end{pmatrix}とすると、各固有ベクトルは「正規(長さが1)直交(ベクトルの内積が0)基底」であるため、これを列ベクトルに持つ行列Uは直交行列である。直行行列の逆行列は、転置行列と等しいため、
URU^T=
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{pmatrix}
と表せる。
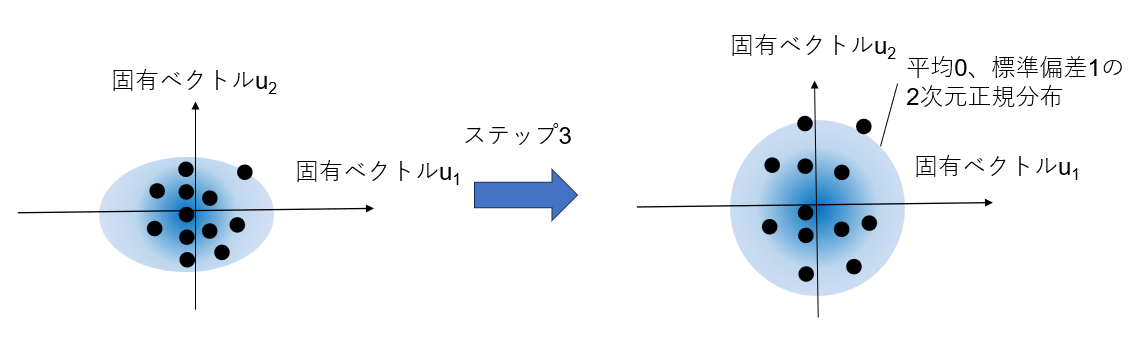
ここで行ったことのイメージはこんな感じ。

ステップ3:主成分方向に標準化する
ステップ1ではデータを標準化したが、ここでは主成分方向の標準化を行う。上の図からも直感的に分かるが、標準化したデータが、主成分方向に引き伸ばされている。つまり、平均は0のままだが、標準偏差が1ではない。そこで、標準化しようという魂胆である。
第一主成分、第二主成分をそれぞれz_1,z_2とすると、
z_1=\bm{y_i}\bm{u_1^T} =(y_{i,圧力},y_{i,水温}) \bm{u_1^T} \\
z_2=\bm{y_i}\bm{u_2^T} =(y_{i,圧力},y_{i,水温}) \bm{u_2^T}
と表せる。標準偏差はそれぞれの固有値倍されているので、第一主成分、第二主成分方向の分散は\lambda_1,\lambda_2である。そのため、標準化を行うと、\frac{z_1}{\sqrt{\lambda_1}},\frac{z_2}{\sqrt{\lambda_2}}と表せる。
ステップ4:カイ二乗検定を行い、異常データを求める
各主成分方向の標準化データが求まったので、これを2乗し、和を求めることで、長さが分かる。標準正規分布N(0,1)の2乗でピンと来ると思うが、検定方法はカイ二乗検定を行うことで異常値が分かる。さて、標準データの2乗和(カイ二乗分布同士の和もカイ二乗分布)を展開して書いてみよう。
\begin{align*}
\frac{z_1^2}{\lambda_1}+\frac{z_2^2}{\lambda_2}
&=
(z_1,z_2)
\begin{pmatrix}
\frac{1}{\lambda_1} & 0 \\
0 & \frac{1}{\lambda_2}
\end{pmatrix}
\begin{pmatrix}
z_1 \\
z_2
\end{pmatrix}
\\
&=
(y_{i,圧力},y_{i,水温})
U
\begin{pmatrix}
\frac{1}{\lambda_1} & 0 \\
0 & \frac{1}{\lambda_2}
\end{pmatrix}
U^T
\begin{pmatrix}
y_{i,圧力} \\
y_{i,水温}
\end{pmatrix}
\\
&=
(y_{i,圧力},y_{i,水温})
R^{-1}
\begin{pmatrix}
y_{i,圧力} \\
y_{i,水温}
\end{pmatrix}
\\
&=
(y_{i,圧力},y_{i,水温})
R^{-1}
\begin{pmatrix}
y_{i,圧力} \\
y_{i,水温}
\end{pmatrix}
\\
&=
(x_{i,圧力}-\hat{\mu}_{圧力},x_{i,水温}-\hat{\mu}_{水温})\Sigma^{-1}
\begin{pmatrix}
x_{i,圧力}-\hat{\mu}_{圧力} \\
x_{i,水温}-\hat{\mu}_{水温}
\end{pmatrix}
\\
\end{align*}
ここで、\Sigma^{-1}は分散共分散行列の逆行列であり、マハラノビス距離の2乗になっていることが分かる。

ステップ5:異常の原因を考察する
分解して書くことで、何が原因で異常データになっているかが分かりやすい。まず、異常データの\frac{z_1^2}{\lambda_1}と\frac{z_2^2}{\lambda_2}を求めると、どちらの主成分の方向に大きく外れているかが分かる。例として、\frac{z_2^2}{\lambda_2}が大きい(=第2主成分方向に外れている)としよう。第2主成分は固有ベクトル\bm{u_2}=(u_{2,圧力},u_{2,水温})に依存しており、u_{2,圧力}とu_{2,水温}のどちらかが大きい値を取っているなら、その特徴量が異常値でありそうなことが分かる。
実装編:MT法をPythonで実装しよう
今回は上記で用いた圧力と水温に加え、振動数を加えた16個のデータに適応していく(データは仮想のものなので、各自変えてやってみると良いかもしれません)。主成分は第二主成分までとし、MT法を適応してみよう。
実装コード
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df=pd.DataFrame()
df['圧力']=[10,9,8,7,8,4,9,12,11,20,13,5,10,12,12,15]
df['水温']=[21,23,24,25,22,23,23,24,21,23,23,22,25,25,23,24]
df['振動数']=[3,4,2,5,3,4,6,3,2,1,5,3,2,4,3,3.5]
df['圧力の標準y']=(df['圧力']-df['圧力'].mean())/df['圧力'].std()
df['水温の標準y']=(df['水温']-df['水温'].mean())/df['水温'].std()
df['振動数の標準y']=(df['振動数']-df['振動数'].mean())/df['振動数'].std()
corr_mat = df[['圧力','水温','振動数']].corr(method='pearson')
eig, P = np.linalg.eig(corr_mat)
D = np.dot(np.dot(np.linalg.inv(P), corr_mat), P)
z=np.zeros((len(df),3))
for i in range(len(df)):
press=df.loc[i]['圧力の標準y']
temp=df.loc[i]['水温の標準y']
freq=df.loc[i]['振動数の標準y']
y=np.array([press,temp,freq]).T
z[i,:]=np.dot(y,D)
df['第一主成分z1']=z[:,1]
df['第二主成分z2']=z[:,2]
df['第一主成分z1の標準2乗']=df['第一主成分z1']**2/eig[1]
df['第二主成分z2の標準2乗']=df['第二主成分z2']**2/eig[2]
df['異常値']=df['第一主成分z1の標準2乗']+df['第二主成分z2の標準2乗']
データの確認
今回用いた仮想データはこのような感じ。

各要素の確認

異常値の上位5つを黄色で塗りつぶしている。異常値は、自由度4(=(3-1)+(3-1))のカイ二乗分布であり、有意水準10%でも異常データはないことが分かる。異常データではないが、最も異常値が大きかった装置8(index8のデータ)に注目して、何が異常値に寄与しているか確認してみよう。
まず、主成分に注目すると、第一主成分が異常値に寄与していることが分かる。第一主成分の固有ベクトルは(u_{圧力},u_{水温},u_{振動数})=(-0.65565313,0.19170648,0.7303202)であり、圧力と振動数の値に左右されやすいことが分かる。標準化データyを見てみると、圧力よりも振動数の方が絶対値が大きく、装置8は振動数が影響していそうなことが分かる。また、第二主成分も第一主成分よりは低いものの無視できる値ではなさそうなので、同様に考えると、水温の標準化データyも大きいので、水温も影響しているかもしれない。
まとめ
MT法を分解して理解することで、説明可能な結果を出力できるのはMT法の良いところだと思う。今回は固有値を大きい順に並べる作業を手打ちするという、かなり手抜きのコードになっているので、修正して自分なりのコードにしてください。






Discussion