今回もベイズ最適化の記事を書くための前段階記事。回帰というと、線形回帰を思い浮かべるかもしれないが、ベイズ最適化ではガウス過程回帰を用いている。そこで自分用にまとめてみた。
ガウス過程回帰とは
ガウス過程という言葉についてまず考えてみる。こちらのサイトが詳しく書いてあるので、参考にしてほしい。
https://www.jstage.jst.go.jp/article/isciesci/62/10/62_390/_pdf
また、こちらの書籍も参考にした。(amazonに飛ぶのでご注意ください)
https://www.amazon.co.jp/ウェブ最適化ではじめる機械学習-―-Bテスト、メタヒューリスティクス、バンディットアルゴリズムからベイズ最適化まで-飯塚-修平/dp/4873119162
自分なりの雑な解釈だと、ガウス過程回帰=ガウス過程+ベイズ線形回帰。ガウス過程とは「対称かつ正定値行列の分散共分散行列\Sigma」と「平均値ベクトル\bm{\mu}」というパラメータが多次元ガウス分布に従うことである。そして、ベイズ線形回帰とは「ベイズ推定」と「線形回帰」を組み合わせた回帰手法を指す。
ガウス過程回帰の理論
最小二乗法による線形回帰では、誤差二乗和が最も小さくなるような関数を一つ求めていたが、ベイズ線形回帰では、入力データ(事前データ)から最も確率高い関数を一つ求めていく手順を繰り返し行う。
(仮定)
・重みパラメータ\bm{w}は確率変数であり、多次元ガウス分布N(\bm{\mu},\Sigma)に従う
・目的変数\bm{y}はガウス分布N(\theta,\sigma^2)に従う
(手順概要)
1.ある基底関数\phiによるデータ\phi(\bm{x})と重みパラメータで\bm{w}を用意。
2.目的変数\bm{y}は\bm{y}=\phi(\bm{x}) \bm{w}という関係にある。
※ここからもガウス分布\bm{w}の線形結合から\bm{y}もガウス分布であることが分かる。
3.事前確率・尤度関数を求め、事後確率を求める。
簡単に図にするとこんな感じ。

では、数式を使ってもうちょっと正確に事前確率と尤度関数を書き下していく。まず、時系列が分かるようにデータセットD(t)=(\bm{x}_1,y_1),・・・,(\bm{x}_t,y_t)とし、尤度関数を書き換えると下記の様になる。
p(D(t)|\bm{w})=\prod_{i=1}^t N(\phi(\bm{x}_i)^T \bm{w},\sigma^2)
次に、時刻0の重みパラメータ\bm{w}の確率密度関数である多次元正規分布をN(\bm{\mu_0},\Sigma_0)とすると、事前確率は次のように書ける。
p(\bm{w})=N(\mu_0,\Sigma_0)
=\frac{1}{(2 \pi)^{\frac{n}{2}} \sqrt{|\Sigma|}} exp(- \frac{1}{2} (\bm{w}-\bm{\mu})^T \Sigma^{-1} (\bm{w}-\bm{\mu}))
下準備は整ったので、ここから事後確率を求めていく。
\begin{align*}
p(\bm{w}|D(t)) &\propto p(\bm{w})p(D(t)|\bm{w}) \\
&\propto N(\mu_0,\Sigma_0) \prod_{i=1}^t N(\phi(\bm{x}_i)^T \bm{w},\sigma^2) \\
&\propto exp(- \frac{1}{2} (\bm{w}-\mu_0)^T {\Sigma_0}^{-1} (\bm{w}-\mu_0) - \frac{1}{2 \sigma^2} (\bm{y}-\Phi^T \bm{w})^T (\bm{y}-\Phi^T \bm{w})) \\
&\propto exp(- \frac{1}{2} (\bm{w}^T {\Sigma_0}^{-1} \bm{w} - \bm{w}^T {\Sigma_0}^{-1} \mu_0 - \mu_0^T {\Sigma_0}^{-1} \bm{w}) - \frac{1}{2 \sigma^2} (- \bm{y}^T {\Phi}^T \bm{w} - (\Phi^T \bm{w})^T \bm{y} + (\Phi^T \bm{w})^T (\Phi^T \bm{w})) \\
&= exp(- \frac{1}{2} (\bm{w}^T {\Sigma_0}^{-1} \bm{w} - 2 \mu_0^T {\Sigma_0}^{-1} \bm{w} - \frac{2}{\sigma^2} \bm{w}^T \Phi \bm{y} + \frac{1}{\sigma^2} \bm{w}^T \Phi \Phi^T \bm{w})) \\
&= exp(- \frac{1}{2} (\bm{w}^T ({\Sigma_0}^{-1} + \frac{\Phi^T \Phi}{\sigma^2}) \bm{w} - 2 \bm{w}^T (\Sigma_0^{-1} \mu_0 + \frac{\Phi^T \bm{y}}{\sigma^2})) \\
\end{align*}
ここでA={\Sigma_0}^{-1} + \frac{\Phi^T \Phi}{\sigma^2}, \bm{b}=\Sigma_0^{-1} \mu_0 + \frac{\Phi^T \bm{y}}{\sigma^2}とし、定数exp(\bm{b}^T (A^{-1})^T \bm{b})をかけると
\begin{align*}
p(\bm{w}|D(t)) &\propto exp(- \frac{1}{2} (\bm{w} - A^{-1} \bm{b})^T A (\bm{w} - A^{-1} \bm{b})) \\
\end{align*}
となり、ガウス分布の形を取っていることが分かる。これより時刻tの各パラメータをまとめる。ここで上付き文字の-1は逆行列を表している。後でもこの話をするので、「逆行列が登場している」ことを頭にとどめておいてほしい。
\bm{\mu}_t=A_t^{-1} \bm{b}_t \\
\Sigma_t=A_t^{-1} \\
A_t={\Sigma_0}^{-1} + \frac{\Phi^T \Phi}{\sigma^2} \\
\bm{b}_t=\Sigma_0^{-1} \mu_0 + \frac{\Phi^T \bm{y}}{\sigma^2}
参考までに、新サンプルが得られた時のベイズ更新についても考えてみる。これらを時刻t+1のときと組み合わせると
\bm{\mu}_{t+1}=A_{t+1}^{-1} \bm{b}_{t+1} \\
\Sigma_{t+1}=A_{t+1}^{-1} \\
A_{t+1}=A_t + \frac{1}{\sigma^2} \phi(\bm{x_{t+1}})^T \phi(\bm{x_{t+1}})\\
\bm{b}_{t+1}=\bm{b}_t + \frac{1}{\sigma^2} \phi(\bm{x_{t+1}}) y_{t+1}
話の腰が折れてしまったが、これでパラメータ\bm{w}の事後分布が完成した。これにより、新しい入力値\bm{x}_*の出力データy_*の事後分布も求めることができる。まずは、y_*の期待値\theta_*の事後分布を求めてみよう。上記図にもチラッと書いているが、\theta=\phi(\bm{x})^{T}\bm{w}より、
\begin{align*}
E[\theta_*|\bm{x_*}]&=E[\phi(\bm{x})^{T}\bm{w}]\\
&= \phi(\bm{x})^{T} E[\bm{w}] \\
&= \phi(\bm{x})^{T}\bm{\mu_t}
\end{align*}
次に分散V[\theta_*|\bm{x_*}]を考える。
\begin{align*}
V[\theta_*|\bm{x_*}]&= V[(\phi(\bm{x_*})^{T}\bm{w}-\phi(\bm{x_*})^{T}\bm{\mu_t})(\phi(\bm{x_*})^{T}\bm{w}-\phi(\bm{x_*})^{T}\bm{\mu_t})^{T}] \\
&= V[(\phi(\bm{x_*})^{T}(\bm{w}-\bm{\mu_t})) (\phi(\bm{x_*})^{T}(\bm{w}-\bm{\mu_t})) ^{T} \\
&= \phi(\bm{x_*})^{T} E[(\bm{w}-\bm{\mu_t})(\bm{w}-\bm{\mu_t})^{T}] \phi(\bm{x_*}) \\
&= \phi(\bm{x_*})^{T} V[\bm{w}] \phi(\bm{x_*}) \\
&= \phi(\bm{x_*})^{T} \Sigma_t \phi(\bm{x_*})
\end{align*}
よって、出力データ\bm{y}の期待値\theta_*は\theta_* \sim N(\phi(\bm{x})^{T}\bm{\mu_t},\phi(\bm{x_*})^{T} \Sigma_t \phi(\bm{x_*}) )となる。また、上記は一つの入力データ\bm{x_*}に対する\theta_*であるが、N個の入力データX_*=(\bm{x_{*,1}},・・・,\bm{x_{*,N}})^Tに対するN個の出力データ\bm{\theta_*}=(\theta_{*,1},・・・,\theta_{*,N})^Tは次のように表せる。ここで計画行列\Phi_*=(\phi(\bm{x_{*,1}}),・・・,\phi(\bm{x_{*,N}}))^Tとしている。
\bm{\theta_*} \sim N(\Phi_*\bm{\mu_t},\Phi_* \Sigma_t \Phi_*^T)
また、期待値だけでなく新しい出力データy_*も正規分布であり、平均値は\theta_*、分散は\theta_*の分散\phi(\bm{x_*})^{T} \Sigma_t \phi(\bm{x_*})にy_*自身の分散\sigma^2を足したものなので、次のように表せる。
y_* \sim N(\phi(\bm{x})^{T}\bm{\mu_t},\sigma^2 + \phi(\bm{x_*})^{T} \Sigma_t \phi(\bm{x_*}) )
これで、パラメータ\bm{w}の事後分布、新入力データ\bm{x}_*に対する新出力データy_*やその期待値\theta_*の事後分布が求められるようになった。お疲れ様です。
といいたいところだが、\bm{\mu}_t,\Sigma_tはもう少し書き下せる。まず、下記のウッドベリーの公式を使う。
(A+BDC)^{-1}=A^{-1}-A^{-1}B(D^{-1}+CA^{-1}B)^{-1}CA^{-1}
ここでA=\Sigma_0^{-1},B=\Phi^T,C=\Phi,D=\sigma^{-2}Iとすると
(\Sigma_0^{-1}+\sigma^{-2}\Phi^{T}\Phi)^{-1}=\Sigma_0-\Sigma_0\Phi^{T}(\sigma^{2}I+\Phi\Sigma_0\Phi^{T})^{-1}
となるので、
\begin{align*}
\bm{\mu_t}&=(\Sigma_0-\Sigma_0\Phi^{T}(\sigma^{2}I+\Phi\Sigma_0\Phi^{T})^{-1}\Phi\Sigma_0)(\Sigma_0^{-1}\bm{\mu_0}+\sigma^{-2}\Phi^{T}\bm{y}) \\
\Sigma_t&=\Sigma_0-\Sigma_0\Phi^{T}(\sigma^{2}I+\Phi\Sigma_0\Phi^{T})^{-1}\Phi\Sigma_0
\end{align*}
よって上記式は次のようになる。
\begin{align*}
E[\theta_*|\bm{x}_*] &=\Phi_* \bm{\mu_t} \\
&= \Phi_* (\Sigma_0-\Sigma_0\Phi^{T}(\sigma^{2}I+\Phi\Sigma_0\Phi^{T})^{-1}\Phi\Sigma_0)(\Sigma_0^{-1}\bm{\mu_0}+\sigma^{-2}\Phi^{T}\bm{y}) \\
&= \sigma^{-2} \Phi_* \Sigma_0(\Phi^{T}-\Phi^{T} (\sigma^{2}I+\Phi\Sigma_0\Phi^{T})^{-1}\Phi \Sigma_0 \Phi^{T})\bm{y} \\
&= \sigma^{-2} \Phi_* \Sigma_0 \Phi^{T}((\sigma^{2}I+\Phi\Sigma_0\Phi^{T})^{-1}((\sigma^{2}I+\Phi\Sigma_0\Phi^{T})-\Phi\Sigma_0\Phi^{T}))\bm{y} \\
&= \Phi_* \Sigma_0 \Phi^T (\sigma^2 I + \Phi \Sigma_0 \Phi^T)^{-1} \bm{y}\\
\\
V[\theta_*|\bm{x}_*] &= \Phi^T \Sigma_t \Phi\\
&= \Phi^T (\Sigma_0-\Sigma_0\Phi^{T}(\sigma^{2}I+\Phi\Sigma_0\Phi^{T})^{-1}\Phi\Sigma_0) \Phi \\
&= \Phi_* \Sigma_0 \Phi_*^T - \Phi_* \Sigma_0 \Phi^T (\sigma^2 I + \Phi \Sigma_0 \Phi^T)^{-1} \Phi \Sigma_0 \Phi_*^T
\end{align*}
ここで
\begin{align}
K=\Phi \Sigma_0 \Phi^T \\
K_* =\Phi \Sigma_0 \Phi_*^T \\
K_{**} = \Phi_* \Sigma_0 \Phi_*^T \\
\end{align}
とすると、
E[\theta_*|\bm{x}_*] = K_*^T (\sigma^2 I + K)^{-1} \bm{y} \\
V[\theta_*|\bm{x}_*] = K_{**} -K_*^T (\sigma^2 I + K)^{-1} K_*
これを使えば、データxを更新していけば\thetaの最適解が求められる。ただし、(1)(2)(3)の行列計算が厄介である。\Phiが基底関数の集合体であることもあり、基底関数の数が増えるほど計算が難しくなる。ここで、カーネルトリックという手法を用いる。イメージは下記の通り。

その名の通り、カーネル関数を用いるので、まずはK,K_*,K_{**}がカーネル関数である証明をしなければならない。本来はMercerの定理などを満たすかどうか確認しなければならないが、今回は「内積の形を取るかどうか」という簡易な証明だけを行ってみる。ある入力データx,x_*の時の(1)式は
\begin{align*}
K(x,x_*)&= \phi(x)^T \Sigma_0 \phi(x_*) \\
&= \phi(x)^T (\Sigma_0^{1/2})^T {\Sigma_0^{1/2}} \phi(x_*)
\end{align*}
ここで\varphi(x)={\Sigma_0^{1/2}} \phi(x)とすると
\begin{align*}
K(x,x_*)&= \varphi(x)^T \varphi(x_*)
&= k(x,x_*)
\end{align*}
このようにある特徴空間に入力データを写像したい際の内積を表しており、(1)はカーネル関数k(x,x_*)の形をとっていることが簡易的に分かる。(2)(3)も同様の計算なのでやってみてほしい。このカーネル関数k(x,x_*)には様々な形があり、今回は一般的なガウスカーネル
k(x,x_*)=exp(- \gamma||\bm{x}-\bm{x_*}||^2)
を用いて、実装する。式からも分かるが、煩わしかった\Phiなどの行列計算が消えていることが分かる。
このようにカーネル関数を使うと計算ステップが一つ減る。このことをカーネルトリックという。
また、逆行列についても触れておく。逆行列は基底関数の数が多くなればなるほど時間がかかる。なので、K,K_*,K_{**}を別々に計算することはとても非効率である。
そこで、下記の様に工夫すると高速化を図ることができる(今回の記事ではPython実装は行わない)。Qは\bm{X}同士の各成分の内積を取った行列(\bm{X}の要素数×\bm{X}の要素数)、\deltaは()内の行列の対角要素を行ベクトルで抜き出す関数、T_Nは()内の行ベクトルを行方向にN回繰り返す関数である。
K=exp(- \gamma (T_N(\delta(Q_{\bm{X},\bm{X}}))^T-2 Q_{X,X} + T_N(\delta(Q_{\bm{X},\bm{X}})))) <n×n行列>\\
K_*=exp(- \gamma (T_M(\delta(Q_{\bm{X},\bm{X_*}}))^T-2 Q_{X,X_*} + T_N(\delta(Q_{\bm{X_*},\bm{X_*}})))) <n×m行列>\\
K_{**}=exp(- \gamma (T_M(\delta(Q_{\bm{X_*},\bm{X_*}}))^T-2 Q_{X_*,X_*} + T_M(\delta(Q_{\bm{X_*},\bm{X_*}})))) <m×m行列>
余力がある方は試してみると面白いと思う。
Pythonでの実装コード
では実装してみよう。今回はy=2sin(10x)+3cos(20x)+5sin(4x)というモデルを用意し、ガウス過程回帰で上記モデルを求める。既に観測しているデータ数(事前データ数)と分散(事前データの分散)、新たに得たデータ数(追加データ数)が変化すると回帰結果にどのような影響を及ぼすかを確認するために今回もstreamlitを用いた。コードが短いので、バックエンドとフロントエンドを一つにまとめている。
gaussian-process-regression.py
import numpy as np
from matplotlib import pyplot as plt
import streamlit as st
import time
def gaussian_process(n,New_n,s):
np.random.seed(5)
f = lambda x:2*np.sin(10*x) + 3*np.cos(20*x) + 5*np.sin(4*x)
New_x = np.sort(np.random.random(size=New_n))
New_y=f(New_x) + np.random.normal(0,s**(0.5),size=New_n)
x = np.sort(np.random.random(size=n))
y = f(x) + np.random.normal(0,s**(0.5),size=n)
def gaussian_kernel(x1,x2,gamma=100):
return np.exp(-gamma*(x1-x2)**2)
K=np.zeros((len(x),len(x)))
for i,xi in enumerate(x):
for j,xj in enumerate(x):
K[i,j]=gaussian_kernel(xi,xj)
K_star=np.zeros((len(x),len(New_x)))
for i,xi in enumerate(x):
for j,xj_star in enumerate(New_x):
K_star[i,j]=gaussian_kernel(xi,xj_star)
K_starstar=np.zeros((len(New_x),len(New_x)))
for i,xi_star in enumerate(New_x):
for j,xj_star in enumerate(New_x):
K_starstar[i,j]=gaussian_kernel(xi_star,xj_star)
return New_x,x,y,K,K_star,K_starstar,New_y
with st.form(key="gaussian_process"):
n:int=st.slider("事前データ数", 0, 1000, 100, 10)
New_n:int=st.slider("追加データ数", 0, 1000, 100, 10)
s:int=st.slider("事前データの分散", 0, 10, 1, 1)
submit_button=st.form_submit_button("計算")
if submit_button:
start=time.time()
New_x,x,y,K,K_star,K_starstar,New_y=gaussian_process(n,New_n,s)
A=np.linalg.inv(K+s*np.eye(K.shape[0]))
mu=np.dot(np.dot(K_star.T,A),y)
sigma=K_starstar-np.dot(np.dot(K_star.T,A),K_star)
true_x=np.linspace(0,1,100)
fig, ax = plt.subplots()
plt.fill_between(New_x,mu-2*np.sqrt(np.diag(sigma)),mu+2*np.sqrt(np.diag(sigma)),alpha=0.5,color='gray')
plt.plot(true_x,2*np.sin(10*true_x) + 3*np.cos(20*true_x) + 5*np.sin(4*true_x),color='black',linestyle='dotted',label="true")
plt.plot(New_x,mu,color='black',label="Gaussian process regression")
plt.xlabel(r'$x$')
plt.ylabel(r'$y$')
plt.xlim(0,1)
plt.legend()
end=time.time()
st.title('処理時間',end-start)
st.pyplot(fig)
-
np.linalg.inv(K+s*np.eye(K.shape[0]))で何をやっているか
np.linalg.inv()は()内の逆行列を求めている。また、np.eye()は()の形の単位行列を作る。
-
plt.fill_between(New_x,mu-2np.sqrt(np.diag(sigma)),mu+2np.sqrt(np.diag(sigma)),alpha=0.5,color='gray')で何をやっているか
回帰曲線から±2σの範囲をグレーで塗りつぶしている。また、引数のalphaは透過度を指す。
結果・考察
まず、実装・出力画面は下記の様になる。

実装画面

出力結果例
実線が回帰曲線、破線がモデルy=2sin(10x)+3cos(20x)+5sin(4x)、グレー部分が±2σの範囲(95%信頼区間)を表している。気づいたことは下記の通り。
・事前・追加データ数が多くなるほど、Trueに近くなる
→yの平均値式内にK_*が登場しており、事前データと追加データ両方に関与していることがここからも分かる。
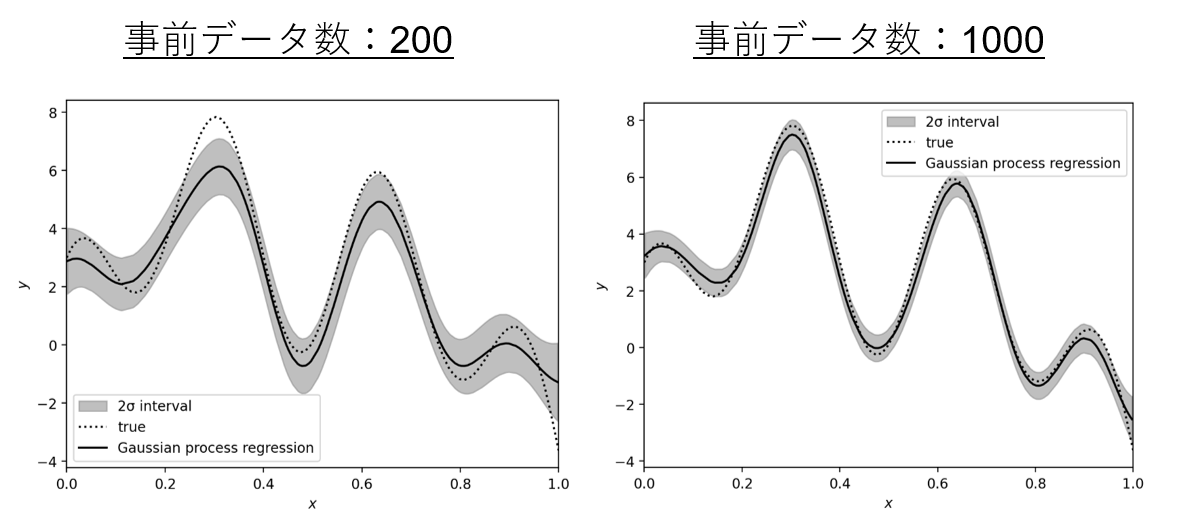
結果①
・事前データの分散σが小さくなるほど、Trueに近くなる
→事前データ数を増やす操作は、分散σを小さくするうえで有効。
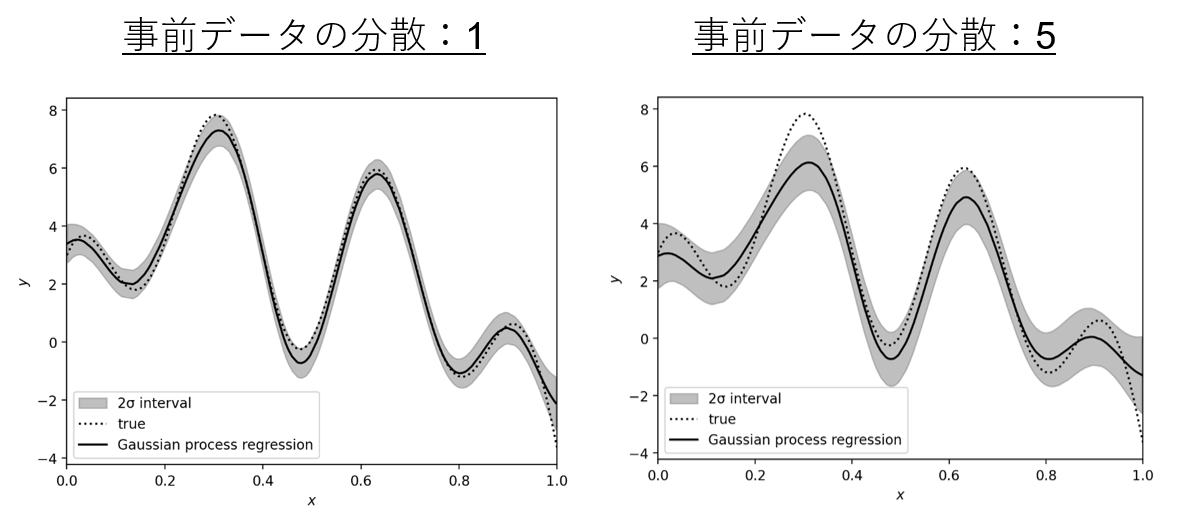
結果②
・追加データよりも事前データが増える方が導出に時間がかかる
→行列計算の中でも逆行列の計算は特に時間がかかり、(\sigma^2 I + K)^{-1}にかなりの時間がかかっていると思われる。この式内に登場するKは事前データに依存する行列であり、事前データが増えるほど、導出時間が長くなっている。
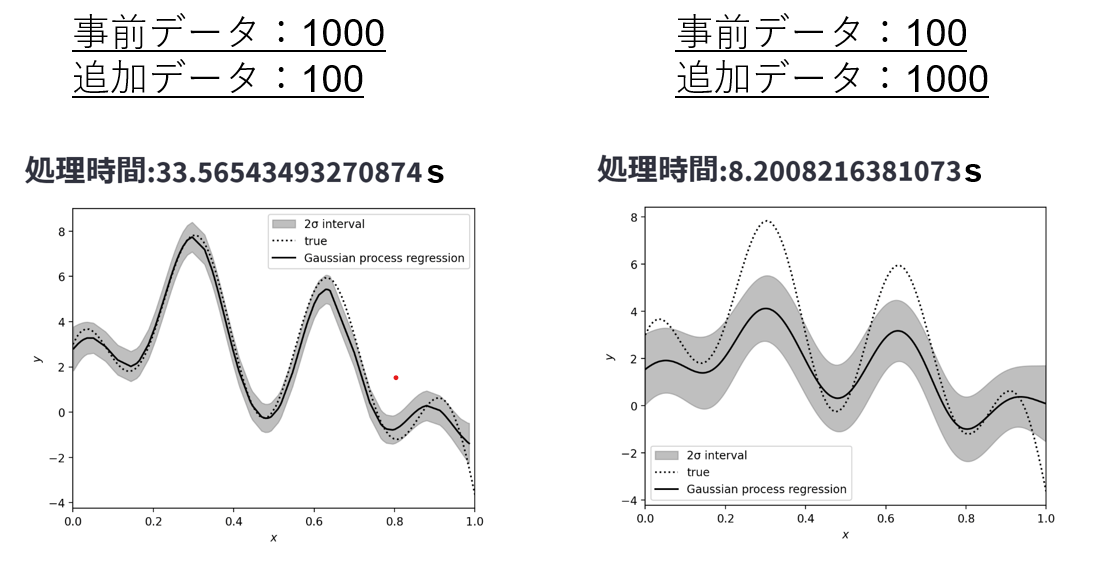
結果③
おまけ(ちょっとした高速化)
上記のK,K_*,K_{**}を一緒に計算する手法じゃなくても簡単に高速化できる。それは上記コードのfor文を下記の様に直すだけ。
高速化
K=np.exp(-gamma*(np.tile(np.diag(Q),(X.shape[1],1)).T-2*Q+np.tile(np.diag(Q),(X.shape[1],1))))
K_star=np.exp(-gamma*(np.tile(np.diag(Q),(X_star.shape[1],1)).T-2*Q_star+np.tile(np.diag(Q_starstar),(X.shape[1],1))))
K_starstar=np.exp(-gamma*(np.tile(np.diag(Q_starstar),(X_star.shape[1],1)).T-2*Q_starstar+np.tile(np.diag(Q_starstar),(X_star.shape[1],1))))
自分の環境だと修正前は解の導出に14秒近くかかっていたが、修正後は0.2秒ぐらいに収まっている。ガウス過程回帰のようにサンプル数が多く、for文で回す回数が多くなる時は、行列でひとまとめに計算してしまおう。お疲れ様でした。







Discussion