分析モデルインプット

データ分析の目的

・理解志向
分析対象がどのような仕組みに基づいて動いているかなど、背景の原理を理解する
→データを眺めて、「初速度０で落下させた物体は、落下距離が落下時間の2乗に比例する」を発見する
・応用志向
分析によって得られた知見を実世界で応用することで、何らかの利益を得ることが目的
→数多の施行で物をどれくらい質量のものをどれくらいの速さで投げれば目標にあたるかを空気抵抗を加味した実世界での応用を考える

分野や状況によって文化や価値観が異なるため、それに応じた分析モデルの選択が重要

ベイズ統計

https://ja.wikipedia.org/wiki/ベイズの定理
時間遡行の条件付確率
本質は、時間の向きを反転させること原因から結果を推定すること
箱Aと箱Bがあり、箱Aの中には赤玉３個、箱Bには白玉が５個入っているとする、ここから無作為に箱を選び一つの球を取り出す
ここで「赤玉を取り出したとき、実は選んだ箱が箱Aであった確率」はいくつか？
⇒玉の色から箱を推論している考える方向と時間の流れが逆向き
⇒原因→結果の自然な方向で考えればよく素直に考えれば確立を計算できる

標準化

回帰分析

単回帰分析
二つの変数を比較して行う分析
→変数間の関係性の「理解」や、変数の値の「予測」、因果関係の探究などに利用する
→「理解」では変数xが変化したときに変数yに影響があるのか？あるとしたらどの程度かを「予測」する
→変数xが変化したときに変数yが変化するか？xからyを予測できるか？という考え方で分析する
変数x（説明変数）を主としてy（従属変数）を従とする
→主従の関係は分析の目的や分析対象によって人が設定する

・y = ax + b + ζという線形の関係性を仮定する（回帰直線）
x: 説明変数, y: 従属変数、ζ： 誤差を表す確率変数
→xが増えるとyが増えるあるいは減る
→良い感じのa,bを見つける
→教師データや訓練データを用いて、無数にあるパラメータの組み合わせから最適な数値を選ぶ（推定）

最小二乗法

手元にあるx,yの組のデータを（x1,y1）,(x2,y2)...(xn,yn)とし、誤差ζ＝y-(ax+b)を二乗してプラスマイナスを打ち消し、その和を最小にするパラメータa,bを選択する

この公式を用いることで機械学習よりも圧倒的に簡単に推定することができる

重回帰分析

説明変数が複数ある回帰分析
・y = a1x1 + a2x2 + ... + amxm + b + ζという線形の関係性を仮定する
x1,x2...xm: 説明変数, y: 従属変数、ζ： 誤差を表す確率変数
定数a1,a2...am, bの値を考える
a1,a2...ai...amパラメータは偏回帰係数と呼び、ａｉは一つの変数の値だけが異なる場合にｙの値がどの程度異なるのかを表す量
偏回帰係数の意味を解釈する場合、説明変数の間の相関関係や因果関係ないかどうか注意する

多重共線性

相関が非常に高い説明変数たちがある時、背後の原因は一つかもしれないのに計算上は複数回登場してしまうので過剰に係数が重くなってしまうかもしれない
→不安定な推定: 予測変数間の高い相関により、回帰係数の推定が不安定になり、データに小さな変化があっただけで大きく変動することがある
→多重共線性への対処
・変数同士の相関関係を見る
・推定結果を見る
→偏回帰係数の推定結果を見て、多重共線性がないかを疑ってみる
・VIFを確認する

VIFのどれかひとつが10を超えていたら多重共線性が起こっている、チェックできる

回帰分析の精度指標

分析結果の評価とは、分析の目的や仮設と分析結果を比較する中で、結果の良しあしを判断する

RMSE

大まかな誤差の大きさを表す
→分析モデルの誤差の二乗の平均をルートとる
→誤差を2乗して全てを0以上に
→その平均をとり、おおよその誤差の二乗の大きさを見積もる
→そのルートをとり、おおよその誤差の大きさを見積もる
実は誤差の平均は0になり、標準偏差がRMSEとなるので大まかな誤差の大きさを表す

決定係数

被説明変数yの値の大小を決める要因全体のうち、説明変数に含まれる要因の割合を表す指標
→データに対する、推定された回帰式の当てはまりの良さ（度合い）を表します
ここを参照するべし（https://bellcurve.jp/statistics/course/9706.html）

これらの精度指標を計算するだけでは、分析モデルの良し悪しを図れない

機械学習を使う

関数探索を機械に任せるので解釈が及ばない結果になる
→機械学習の利用は、分析モデルの完全な制御下に置くことをあきらめ、その代わりに自身の想像以上の結果をを狙うこと

決定木

2択や多択の連続で分類問題や回帰問題を解く分析モデル

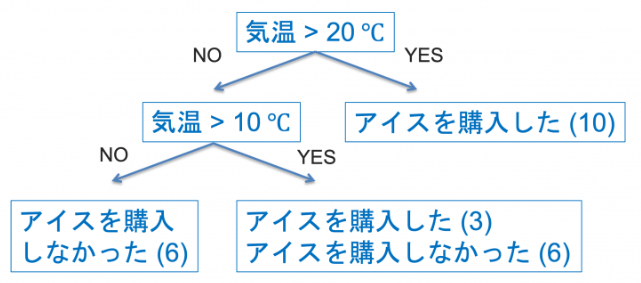
→属性やパラメータの大小をもとに選択を繰り返し、結果を予測する分析モデル
・決定木の学習と推論
どの変数でどのように分割するともっとも良く分離できるか？を考える
→与えられたデータに対して、選択の連続を適用していくとどこかの葉に至ります。

ランダムフォレスト

決定木をたくさん作り、それらの多数決によって分類問題を解く分析モデル
→決定木モデルの場合、分析が雑すぎる問題がある。
→ランダムフォレストでは多数の決定木を用いることでカバーして補完し、精度を高める
→多数のモデルを統合してモデルを作成（アンサンブル学習）

勾配ブースティング決定木

ランダムフォレストをさらに改善したモデル
→ランダムフォレストでは、雑な分析の一本目と詳細に分析された一本目の木が同じ１票を持つ多数決になる
→本来なら二本目の木のほうが強い発言権をもつべき
→この問題を解消するために、多数決における発言権の強さを学習可能なパラメータに加える
→学習時にそれぞれの葉に「～の自信度」に対応する数値を割り振る

木系モデル使い分け

・決定木
→複雑な問題に対する対処能力は低いが、データ数が数十件程度でも良い分析結果を出す
・勾配ブースティング決定木
→最も高い柔軟性を持つ分析モデル、高速化に応じて数十億のデータでも現実的な時間で動作し、高い精度を誇る
→変数の数、データの量も大量な場合活躍する
・ランダムフォレスト
→sckit-learnに実装があり容易に実行できる
→中間的な位置のモデルなのでベースラインのモデルを作るなのどの利用もできる

特徴量エンジニアリング

木系モデルは二つ以上の変数を合成した変数の利用が苦手
→x + yの符号によって〇と×が決まるデータがあるとすると、木系のモデルの場合何度もデータ分割を繰り返さないといけない
→説明変数にx + yを加えることで回避できる
→既存の変数の組み合わせで新しい変数を作り、分析モデルの精度向上を図る（特徴量エンジニアリング）

決定木の解釈

・決定木は機械学習アルゴリズムでは珍しく、高い解釈性をもつ
・手元にある教師データと過度に適合してしまい、課題に対する解決能力を欠いてしまう現象（過学習）がおこる
→過学習が起こっている場合、新しいデータに対するモデルの推論結果の精度は低くなる。
→「新しいデータに対するモデルの推論制度」を汎化性能

ハイパーパラメータチューニング

・過学習に対処するために、モデルにメタ情報を指定するパラメータ（ハイパーパラメータ）
→「分岐の回数は各データ5回まで」、「葉の枚数は16枚」の5、16などの数字
→最適なモデルを得る→ハイパーパラメータチューニング

ノンパラメトリック手法

・k近傍法
説明変数xに対して被説明変数yを予測する
→教師データ(x1,y1),(x2,y2),(x3,y3)...,(xn,yn)の中で説明変数xiがxに近いほうから順番にk個選び、それらに対応するyiの平均や多数決を予測値とする
→近いデータをk個集めて、そのk個のデータを見て決める
これをさらに発展させたのがカーネル密度推定法
・カーネル密度推定法
→各データ点を中心とした確率分布を用紙し、これらの平均をとる確率分布を推定する

統計基礎

累積相対度数（各相対度数を足し合わせたもの）の偏りの曲線ローレンツ曲線
→数値で表すとジニ係数
・ジニ係数が0
→20％の都道府県内に全国の総スクリーン数の20％がある、同じく30パーセントの都道府県には30％の…
という状態
・ジニ係数が1
→映画館が一つしかなくその映画館が日本のすべての映画を放映している

トリム平均

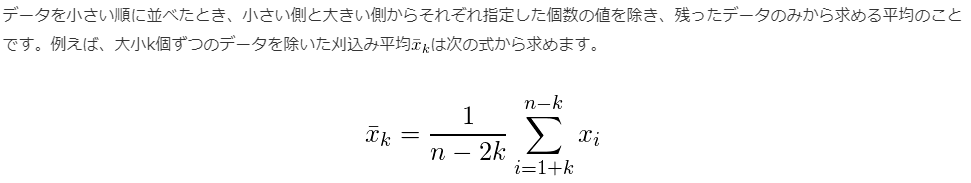
深層学習

→深層学習は数学的な枠組みはシンプルだが、すごい技術
→どんなAIもただの関数
例えば画像分類器の場合すべての画像データは0と1の集まりで、「犬である」「猫である」という出力も０と１の数値の集まり
→画像分類器は数値を数値に変換する仕組み
「犬」、「猫」、「車」、「テーブル」などの分類結果に対する１０００通りのラベル分類を考える
→画像分類器は与えられた画像がそれぞれのラベルに属する確率p1,p2,p3......p１０００を計算しその確率が最大になるものを出力する。1000次元ベクトルｐ ＝ （p1,p2,....p1000)
→画像分類器は3000次元ベクトルxを1000次元のベクトルpに変換する関数をp=f(x)になる

自然言語処理

人間が通常日常的に使う言語を自然言語
→分析することを総称して自然言語処理

テキストデータを分析したい
・データをとりあえずたくさん読む
・長さに着目する
→データがアンケートの自由記述だった場合、その文字数には対象への愛の量が現れる
→文章の長さによってデータ生成の背景にある法則が異なるということであり、文章の長さによって質が異なる
・単語の登場回数を数える
→単語の登場回数を数えれば文章の分類を簡単に行える

自然言語処理と表現学習

単語や文章をベクトルで表現→分散表現
・文章や単語の意味は単語数よりはるかに少ない要素で表現できる
・意味を捉えたベクトルが作成できれば、その後の分析は何でもできる
機械に意味を理解させたい。そしてそれは低次元ベクトルで行われるはず

ウェルチの検定

2つの母集団から取ってきた標本の標準平均に差があった→母平均にも差があるか？
ex.薬Aと薬Bが効くまでの日数
等分散を仮定

数学のテスト
・A県の40人、平均63、不変分散5の二乗
・B県の60人、平均58、不変分散10の二乗
両方とも正規分布、等分散
A県の高校生はB県の高校生よりも優秀といえるか？優位水準１％で検定せよ

帰無仮説：母平均は等しい
対立仮設：Aの母平均＞Bの母平均

自由度98のt分布（40＋60－2）を考える

・等分散を仮定しない場合（ウェルチの検定）
帰無仮説：母平均は等しい
対立仮設：Aの母平均＞Bの母平均
確率変数Tの自由度92のt分布

中心極限定理（ちゅうしんきょくげんていり）とは、どんな母集団からでも、十分に大きいサンプルサイズを取ると、そのサンプルの平均は正規分布（ベルカーブの形をした分布）に近づくという統計の法則です。この定理により、母集団の分布がどんな形であっても、サンプルの平均が正規分布に従うと見なせるため、多くの統計解析が可能になります。

• 中心極限定理

母集団からn個とって標本平均を求める

→母集団の分布は関係なく、どの母集団でも正規分布になる

中心極限定理は誤差を数学的に評価する背景にある