サポートベクターマシンをPythonコードを交えて紹介

はじめに

PRML(Pattern Recognition and Machine Learning)でハードマージンのサポートベクターマシンについて学んだ内容をまとめて、pythonで実装しました。主に7章1節の内容です。より一般的なソフトマージンのモデルについては扱っていません。そのほか参考になるものは記事の一番下にのせてあります。

理論

問題設定

N個の既知のデータの組$((\mathbf{x}_1, t_1), ... (\mathbf{x}_N, t_N)), t_i \in \{-1, 1\}$があります。今、新しく$\mathbf{x}_{N+1}$を知った時、$t_{N+1}$を予測したいです。

サポートベクターマシンの目標

$\mathbf{\phi}(\mathbf{x}) = (\phi_1(\mathbf{x}), \phi_2(\mathbf{x}), ... , \phi_M(\mathbf{x}))^T$という特徴量を用いた線形モデルを考えます。

$$\begin{aligned} y(\mathbf{x}) = \mathbf{w}^T\mathbf{\phi}(\mathbf{x}) + b \end{aligned}$$

今、訓練データが特徴量空間において線形分離可能だと仮定します。このとき、定義より少なくとも一つの$\:t_ny(\mathbf{x}_n) \gt 0 \quad n = 1, ... , N\:$となる$\mathbf{w}, b$が存在します。基本的にこのような$\mathbf{w}, b$は無数に存在しますが、その中で汎化誤差ができるだけ小さいものを求めたいです。

線形分離可能とは
このM次元の特徴量空間で、M-1次元の超平面のなかで、片側に$t_n = 1$となる$\mathbf{\phi}(\mathbf{x}_n)$が、もう片側に$t_n = -1$となる$\mathbf{\phi}(\mathbf{x}_n)$のみが分布するようなものが存在する時、そのデータは線形分離可能といいます。

サポートベクターマシンのアプローチは、$y=0$となる超平面と訓練データの最短の距離であるマージンを最大にすることで、最適な$\mathbf{w}, b$を決めるというものです。

制約付き最適化問題に落とし込む

データ点と超平面の距離は以下のようになるので、

$$\begin{aligned} \frac{|\mathbf{w}^T\mathbf{x} + b|}{||\mathbf{w}||} = \frac{t_n(\mathbf{w}^T\mathbf{\phi}(\mathbf{x}_n) + b)}{||\mathbf{w}||} \end{aligned}$$

マージンが最大となる$\mathbf{w}, b$は以下になります。

$$\begin{aligned} \underset{\mathbf{w}, b}{max}\{\frac{1}{||\mathbf{w}||}\underset{n}{min}[t_n(\mathbf{w}^T\mathbf{\phi}(\mathbf{x}_n) + b)]\} \end{aligned}$$

今、$\kappa \gt 0$を用いて$\mathbf{w} \rightarrow \kappa\mathbf{w} \: and \: b \rightarrow \kappa b$としても各データ点と超平面の距離は変わらないので、超平面に最も近いデータ点に対して、

$$\begin{aligned} t_n(\mathbf{w}^T\mathbf{\phi}(\mathbf{x}_n) + b) = 1 \end{aligned}$$

となるように$\mathbf{w}, b$を取ることにします。このとき、

$$\begin{aligned} t_n(\mathbf{w}^T\mathbf{\phi}(\mathbf{x}_n) + b) \ge 1 \quad n = 1, ... , N \quad \cdots (\spadesuit) \end{aligned}$$

となります。$\frac{1}{||\mathbf{w}||}$を最大化することは、$||\mathbf{w}||^2$を最小化することと等しいので、

$$\begin{aligned} \underset{\mathbf{w}, b}{min}\frac{1}{2}||\mathbf{w}||^2 \end{aligned}$$

を制約の下で考えればよいです。

解くべき問題(1)

$$\begin{aligned} &\underset{\mathbf{w}, b}{min}\frac{1}{2}||\mathbf{w}||^2 \\ subject \: to \quad &t_n(\mathbf{w}^T\mathbf{\phi}(\mathbf{x}_n) + b) \ge 1 \end{aligned}$$

制約付き最適化問題をカーネル関数を用いて表す

解くべき問題(1)を解いてもいいのですが、ここでは最適化問題から$\mathbf{\phi}(\mathbf{x}_n)$を消去し、カーネル関数$k(\mathbf{x}_n, \mathbf{x}_m) = \mathbf{\phi}(\mathbf{x}_n)^T\mathbf{\phi}(\mathbf{x}_m)$の関数の形で表すことを目標にします。そうすることで、$\mathbf{\phi}(\cdot)$によって間接的に定義するだけでなく、直接的に正定値カーネルを定義することができるようになります。

$a_n \ge 0$として、以下のラグランジュ関数を考えます。

$$\begin{aligned} L(\mathbf{w}, b, \mathbf{a}) = \frac{1}{2}||\mathbf{w}||^2 - \sum^N_{n=1}a_n\{t_n(\mathbf{w}^T\mathbf{\phi}(\mathbf{x}_n) + b) - 1\} \end{aligned}$$

このとき、

$$\begin{aligned} \underset{\mathbf{a} \ge \mathbf{0}}{max}L(\mathbf{w}, b, \mathbf{a}) = \left\{ \begin{array}{ll} \frac{1}{2}||\mathbf{w}||^2 & if \: t_n(\mathbf{w}^T\mathbf{\phi}(\mathbf{x}_n) + b) \ge 1 \\ +\infty & otherwise \end{array} \right. \end{aligned}$$

であるので、解くべき問題(1)は次のように書き換えられます。

解くべき問題(2)

$$\begin{aligned} &\underset{\mathbf{w}, b}{min}\:\underset{\mathbf{a}}{max}L(\mathbf{w}, b, \mathbf{a}) \\ subject \: to \quad &\mathbf{a} \ge \mathbf{0} \end{aligned}$$

解くべき問題(2)のことを主問題といいますが、以下の問題のことを双対問題といいます。

$$\begin{aligned} &\underset{\mathbf{a}}{max}\:\underset{\mathbf{w}, b}{min}L(\mathbf{w}, b, \mathbf{a}) \\ subject \: to \quad &\mathbf{a} \ge \mathbf{0} \end{aligned}$$

今回は最小化したい関数とその制約が（適当な条件を満たす）凸関数であったことから主問題と双対問題の解が一致するので、解くべき問題(2)は次のように書き換えられます。

解くべき問題(3)

$$\begin{aligned} &\underset{\mathbf{a}}{max}\:\underset{\mathbf{w}, b}{min}L(\mathbf{w}, b, \mathbf{a}) \\ subject \: to \quad &\mathbf{a} \ge \mathbf{0} \end{aligned}$$

$L(\mathbf{w}, b, \mathbf{a})$は$\mathbf{w}, b$に関して、2次式であるので$L(\mathbf{w}, b, \mathbf{a})$の$\mathbf{w}, b$に関する微分が0となるところが最小値となるため、

$$\begin{aligned} \frac{\partial L(\mathbf{w}, b, \mathbf{a})}{\partial \mathbf{w}} = 0 &\Leftrightarrow \mathbf{w} = \sum^N_{n=1}a_nt_n\mathbf{\phi}(\mathbf{x}_n) \quad \cdots (\clubsuit) \\ \frac{\partial L(\mathbf{w}, b, \mathbf{a})}{\partial b} = 0 &\Leftrightarrow \sum^N_{n=1}a_nt_n = 0 \end{aligned}$$

これらを代入して制約に加えると、

解くべき問題(4)

$$\begin{aligned} &\underset{\mathbf{a}}{max}\sum^N_{n=1}a_n - \frac{1}{2}\sum^N_{n=1}\sum^N_{m=1}a_na_mt_nt_mk(\mathbf{x}_n, \mathbf{x}_m) \\ subject \: to \quad &\mathbf{a} \ge \mathbf{0}, \:\sum^N_{n=1}a_nt_n = 0 \end{aligned}$$

となります。ここで、$k(\mathbf{x}_n, \mathbf{x}_m) = \mathbf{\phi}(\mathbf{x}_n)^T\mathbf{\phi}(\mathbf{x}_m)$です。これで、最適化問題から$\mathbf{\phi}(\mathbf{x}_n)$を消去し、カーネル関数で記述できました。この最適化問題は、凸二次最適化問題と呼ばれていて様々なアルゴリズムで解くことができます。

予測する

$(\clubsuit)$より、

$$\begin{aligned} y(\mathbf{x}) = \sum^N_{n=1}a_nt_nk(\mathbf{x}, \mathbf{x}_n) + b \end{aligned}$$

ここで、$(\spadesuit)$より、$t_n = 1$となる$n$に対して

$$\begin{aligned} &t_n(\sum^N_{m=1}a_mt_mk(\mathbf{x}_n, \mathbf{x}_m) + b) \ge 1 \\ \Rightarrow \: &b \ge t_n - \sum^N_{m=1}a_mt_mk(\mathbf{x}_n, \mathbf{x}_m) \\ \Rightarrow \: &b = \underset{n}{max}\: 1 - \sum^N_{m=1}a_mt_mk(\mathbf{x}_n, \mathbf{x}_m) \end{aligned}$$

この$y(\cdot)$を用いて、新たな入力$\mathbf{x}_{N+1}$に対して、$y(\mathbf{x}_{N+1}) \ge 0$の時$t_{N+1} = 1$と、$y(\mathbf{x}_{N+1}) \lt 0$の時$t_{N+1} = -1$と予測すればいいです。

実装

import文

cvxpyは凸最適化モデリングツールです。制約付き最適化問題をこのライブラリで解きます。

import cvxpy as cp
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification

カーネル

今回はカーネル関数として以下のガウスカーネルを用います。$\gamma = 8$としました。

$$\begin{aligned} k(\mathbf{x}_n, \mathbf{x}_m) = exp(-\gamma||\mathbf{x}_n - \mathbf{x}_m||^2) \end{aligned}$$

def gauss_kernel(x1, x2, gamma=8):
    return np.exp(-gamma * np.dot(x1 - x2, x1 - x2))

以下は、$K_{nm} = k(\mathbf{x}_n, \mathbf{x}_m)$となる行列$K$を作る関数です。

def kernel_matrix(kernel, X):
    K = np.zeros((len(X), len(X)))
    for i in range(len(X)):
        for j in range(len(X)):
            K[i][j] = kernel(X[i], X[j])

    return K

使用するデータ

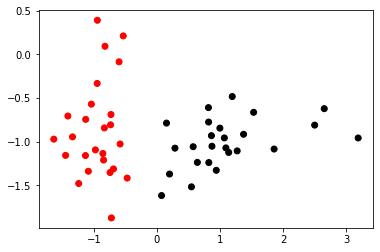
今回はランダムに生成された、入力変数が2次元で目的変数が1か-1である50個のデータを分類します。黒色のデータが$t_n = 1$に、赤色のデータが$t_n = -1$に対応しています。

N = 50
X, t = make_classification(random_state=28,
                           n_samples=N,
                           n_features=2, 
                           n_redundant=0, 
                           n_informative=2,
                           n_clusters_per_class=1,
                           n_classes=2)
t[t == 0] = -1
K = kernel_matrix(gauss_kernel, X)

plt.scatter(X[:,0], X[:,1], c=t, cmap="flag")

制約付き最適化問題を解く

解くべき問題(4)に従います。

# 最適化する変数
a = cp.Variable(N)

# 最適化する関数
obj = cp.Maximize( cp.sum(a) - 1/2 * cp.quad_form(a, (t * K.T).T * t) )

# 制約
constraint = [a >= 0] + [a.T @ t == 0]

# 制約付き最適化問題を解く
prob = cp.Problem(obj, constraint)
prob.solve()

予測

$y(\mathbf{x})$の値を求める関数です。

def predict(a, X, t, b, kernel):
    a = a
    X = X
    t = t
    b = b
    kernel = kernel

    def closure(x):
        ret = b
        for i in range(N):
            ret += a.value[i] * t[i] * kernel(x, X[i])
        return ret

    return closure

$b$の値を求めます。

b = np.max([t[n] - np.sum([a.value[m] * t[m] * K[n][m] for m in range(N)]) for n in range(N) if t[n] == 1])
pre = predict(a, X, t, b, gauss_kernel)

描画の準備です。

NUM = 100
x1_line = np.linspace(-2.5, 3.5, NUM).reshape(-1, 1)
x2_line = np.linspace(-2.5, 1.0, NUM).reshape(-1, 1)
x1_grid, x2_grid = np.meshgrid(x1_line, x2_line)
ps = np.zeros((NUM, NUM))

for (i, x1) in enumerate(x1_line):
    for (j, x2) in enumerate(x2_line):
        ps[j][i] = pre(np.array([x1[0], x2[0]]))

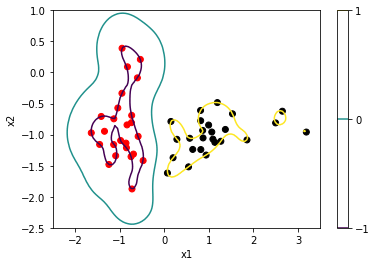
描画コードです。新たな入力$\mathbf{x}_{N+1}$が水色の線の内側にある場合$t_{N+1} = 1$と、そうでない場合は$t_{N+1} = -1$と予測します。

plt.scatter(X[:,0], X[:,1], c=t, cmap="flag")
plt.xlabel('x1')
plt.ylabel('x2')
plt.contour(x1_grid, x2_grid, ps, levels=[-1.0, 0, 1.0])
plt.colorbar()

サポートベクターマシンのスパース性について

この記事の理論の部分では示しませんでしたが、全ての$n = 1, ... , N$に対して$a_n = 0$と$t_ny(\mathbf{x}_n) = 1$のどちらかが成り立ちます。$a_n = 0$となるデータについては予測に関わってこないので、学習が終了した段階で破棄しても問題ありません。また、残った$a_n \gt 0$となるデータをサポートベクトルと呼びます。

参考

書籍

• サポートベクトルマシン　1章

Webサイト

• ソフトマージンのサポートベクターマシンの理論と実装を詳しく解説
• cvxpy
• ソフトマージンの解くべき問題(1)をcvxpyによって解いている
• ラグランジュ双対性について