パーセプトロンアルゴリズムをPythonコードを交えて紹介
はじめに
PRML(Pattern Recognition and Machine Learning)でパーセプトロンアルゴリズム(単純パーセプトロン)について学んだ内容をまとめて、実際のデータを使って学習しました。主に4.1.7の内容です。このアルゴリズムはニューラルネットワークの分野に影響を与えましたが、現在は実用的でないです。
パーセプトロンアルゴリズム
変数一覧と概要
- 訓練データの数
N - 基底関数の数
M - 訓練データの説明変数
\mathbf{X} = \left\{\mathbf{x}_1, \mathbf{x}_2, \cdots \mathbf{x}_N\right\}, \mathbf{x}_n = (x_{n, 1}, x_{n, 2}, \cdots, x_{n_D})^T - 訓練データの目的変数
\mathbf{t} = \left\{t_1, t_2, \cdots t_N\right\} - 基底関数
\mathbf{\phi}(\cdot) = (\phi_0(\cdot), \phi_1(\cdot), \cdots \phi_{M-1}(\cdot))^T - 特徴量
\mathbf{\phi}_n = \mathbf{\phi}(\mathbf{x}_n) = (\phi_0(\mathbf{x}_n), \phi_1(\mathbf{x}_n), \cdots \phi_{M-1}(\mathbf{x}_n))^T - 重みパラメータ
\mathbf{w} = (w_0, w_1, \cdots, w_{M-1})^T
今回は2値分類を行います。入力
線形分離可能とは
あるデータの入力空間の次元を
パーセプトロンアルゴリズムの理論
パーセプトロンアルゴリズムの性質は以下の通りです。
- 全てのデータを正しく2つのクラスに分類する解(先ほど述べた超平面)を求めるアルゴリズム
- 線形分離可能ならば、有限回の計算でその超平面が求まることが保証されている
- 線形分離可能でないならば、解が求まることはない
- 3つ以上のクラスの分類には使えない
以下のような一般化線形モデルを用います。
誤差関数は以下の通りです。
ここで、
確率的勾配降下法によって最適な
ここで、
重みパラメータの更新をわかりやすく
以下のチャートに重みパラメータの更新の挙動をまとめました。
画像を用いて具体的に見ていきます。青い点が
- まずは、
t=+1

- 次に、
t=+1
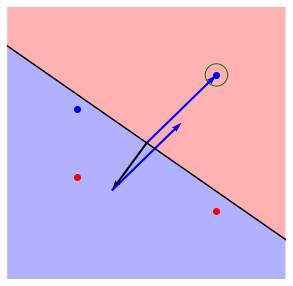
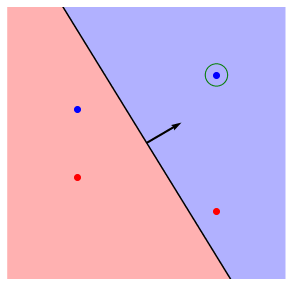
- 次は、
t=-1

- 最後は、
t=+1


この状態がデータを正しく分類できた状態です。これ以降重みパラメータ
アヤメデータセットで学習
import文
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
import seaborn as sns
np.random.seed(28)
使用するデータセット
iris_df_vanilla = sns.load_dataset('iris')
sns.pairplot(iris_df_vanilla, hue = "species", diag_kind="kde")

3種類のアヤメのデータセットです。説明変数は4つです。オレンジ色で示されたversicolorと緑色で示されたvirginicaのデータが混ざり合っていることがわかります。なので、今回はこの2つの種類のアヤメを分類します。
# setosa, virginicam, versicolorの順に50ずつのデータ
iris_df = iris_df_vanilla[50:].sample(frac=1)
y_df = iris_df.loc[:, 'species']
y_df = y_df.replace({'versicolor': 1, 'virginica': -1})
x_vanilla_df = iris_df.loc[:, ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']]
x_df = (x_vanilla_df - x_vanilla_df.mean()) / x_vanilla_df.std()
N = 50
train_x = x_df[:N].to_numpy(copy=True)
train_y = y_df[:N].to_numpy(copy=True)
test_x = x_df[N:].to_numpy(copy=True)
test_y = y_df[N:].to_numpy(copy=True)
100のデータの内、訓練データを50、テスト用データを50に分けました。versicolorがクラス
基底関数
M = 5
def Phi_n_m(xs):
ret = np.ones((len(xs), M))
for n in range(len(xs)):
for m in range(M-1):
ret[n][m+1] = xs[n][m]
return ret
phi_nm = Phi_n_m(train_x)
phi_test = Phi_n_m(test_x)
基底関数は、以下のようにしました。
\phi_0(\mathbf{x}_n) = 1 \phi_1(\mathbf{x}_n) = sepal\_length \phi_2(\mathbf{x}_n) = sepal\_width \phi_3(\mathbf{x}_n) = petal\_length \phi_4(\mathbf{x}_n) = petal\_width
確率的勾配降下法
w_m = np.zeros(M)
for iter in range(1000):
correct_flg = True
for n in range(N):
if np.dot(w_m, phi_nm[n]) * train_y[n] <= 0:
correct_flg = False
w_m = w_m + phi_nm[n] * train_y[n]
if correct_flg:
print(f'end_iteration, w_m | {iter+1}, {w_m}')
break
end_iteration, w_m | 10, [ 1. 0.50993126 0.68519703 -3.27770178 -4.4165233 ]
10回目のループで全ての訓練データが正しく分類されたため、アルゴリズムが止まりました。出力されている
結果
error_count = 0
for i in range(len(test_y)):
error_count += ( np.dot(w_m, phi_test[i]) * test_y[i] <= 0 )
print(error_count)
5
テストデータ50個の内、5個のデータが間違って分類されました。訓練データは全て正しく分類されていることが保証されていますが、テストデータはこのように間違って分類されることがあります。
Discussion