Nadaraya-WatsonモデルをPythonコードを交えて紹介

はじめに

PRML(Pattern Recognition and Machine Learning)でNadaraya-Watsonモデルについて学んだ内容をまとめて、人工的に生成したデータを使って学習しました。主に6.3節の内容です。pythonコードは必要に応じて読んでください。

表記について

• 訓練データの説明変数: $\mathbf{X} = \left\{\mathbf{x_1}, \mathbf{x_2}, \cdots \mathbf{x_N}\right\}, \mathbf{x_n} = (x_{n, 1}, x_{n, 2}, \cdots, x_{n_D})^T$
• 訓練データの目的変数: $\mathbf{t} = \left\{t_1, t_2, \cdots t_N\right\}$
• 新たな入力データ: $\mathbf{x_*}$
• $\mathbf{x_*}$に対する目的変数: $t_*$
• $\mathbf{x_*}$に対する目的変数の予測: $y(\mathbf{x}_*)$

近いデータで予測する

「近い」データを使って、新たな入力データに対する出力を予測することを考えます。

import文

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm

np.random.seed(28)

データ

今回は以下の$t = sin(x) + 0.1x^2$となるデータを使います。

作図コード

line_x = np.linspace(0.0, 2*np.pi, num=500)
line_t = [np.sin(x) + 0.1*x**2 for x in line_x]

plt.plot(line_x, line_t)

次のように45個のデータを生成しました。今回はこれを訓練データとして学習をします。

$$\begin{aligned} t_n = \mathcal{N}(t_n | sin(x_n) + 0.1x^2, 0.25) \end{aligned}$$

作図コード

beta = 0.5

data_x = np.random.rand(45) * 2 * np.pi
data_t = [np.sin(x) + 0.1*x**2 + np.random.normal(0, beta) for x in data_x]

plt.scatter(data_x, data_t)
plt.plot(line_x, line_t)

最近傍法

最近傍法では、訓練データの中でその説明変数と$\mathbf{x_*}$との距離（ユークリッド距離など）が最も近いものの目的変数で$t_*$を予測します。このアルゴリズムでは個々のデータに過度に適合してしまうと考えられます。

k-近傍法

k-近傍法は最近傍法と似ていますが、訓練データの中でその説明変数と$\mathbf{x_*}$との距離が最も近いものから順に$k$個選んで、その算術平均で$t_*$を予測します。適切な$k$の値を選べば、最近傍法より過適合しなくなり、よい予測ができそうです。

下の図で、左上の$k=1$となっているのが最近傍法です。$k$が大きくなるにつれて、予測分布の局所的な変化が小さくなっています。

学習と作図コード

def kNN(k, xs, ts, x_star):
    distance = [[abs(x - x_star), t] for (x, t) in zip(xs, ts)]
    distance.sort()
    t_star = 0
    for i in range(k):
        t_star += distance[i][1]
    t_star /= k
    
    return t_star

def RMSE(true_t, pre_t):
    sum = 0
    for (tt, pt) in zip(true_t, pre_t):
        sum += (tt - pt) ** 2
    rmse = np.sqrt(sum / len(true_t))
    
    return rmse

ks = list(range(1, 21))
kNN_RMSEs = []
nearest_neighbour_ts = [[] for _ in range(len(ks))]

for (i, k) in enumerate(ks):
    for x in line_x:
        nearest_neighbour_ts[i].append(kNN(k, data_x, data_t, x))
    kNN_RMSEs.append(RMSE(line_t, nearest_neighbour_ts[i]))

fig = plt.figure(figsize=(12, 9))

ax1 = fig.add_subplot(2, 2, 1)
ax2 = fig.add_subplot(2, 2, 2)
ax3 = fig.add_subplot(2, 2, 3)
ax4 = fig.add_subplot(2, 2, 4)

ax1.scatter(data_x, data_t)
ax1.plot(line_x, line_t)
ax1.plot(line_x, nearest_neighbour_ts[0], label="k=1")

ax2.scatter(data_x, data_t)
ax2.plot(line_x, line_t)
ax2.plot(line_x, nearest_neighbour_ts[2], label="k=3")

ax3.scatter(data_x, data_t)
ax3.plot(line_x, line_t)
ax3.plot(line_x, nearest_neighbour_ts[8], label="k=9")

ax4.scatter(data_x, data_t)
ax4.plot(line_x, line_t)
ax4.plot(line_x, nearest_neighbour_ts[19], label="k=20")

ax1.legend(loc = 'upper left')
ax2.legend(loc = 'upper left')
ax3.legend(loc = 'upper left')
ax4.legend(loc = 'upper left')

plt.show()

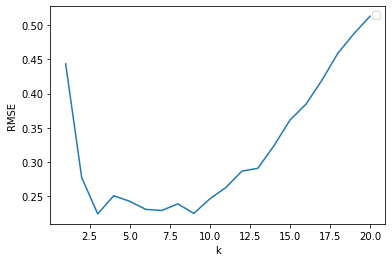
下の図は$k$に対する（真の分布に対する）平均二乗誤差の値を出力していますが、$k$が$3$から$10$くらいのところで誤差が小さくなっていることがわかります。$k$の値は大きすぎても小さすぎてもうまくいかないです。

作図コード

plt.plot(ks, kNN_RMSEs)
plt.xlabel("k")
plt.ylabel("RMSE")
plt.show()

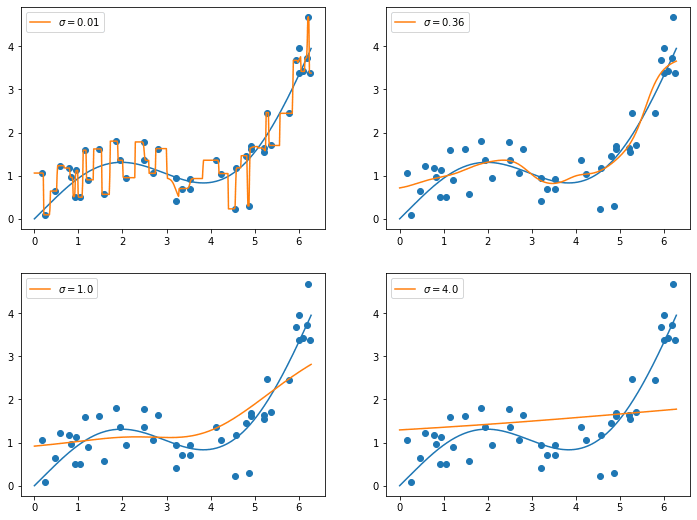
Nadaraya-Watsonモデル

k-近傍法の考え方をもう少し広げてみて、$\mathbf{x_*}$と訓練データとの距離に応じて、重み付けを変える方法を考えてみます。ここで、距離が近いほど大きい値をとるような、近さを表現する非負の関数$g(\cdot)$を考えます。$k(\cdot, \cdot)$を次のように定義します。

$$\begin{aligned} k(\mathbf{x_*}, \mathbf{x_n}) = \frac{g(\mathbf{x_*} - \mathbf{x_n})}{\sum^N_{m=1}g(\mathbf{x_*}- \mathbf{x_m})} \end{aligned}$$

そして、この関数を用いて次のように$t_n$に重み付けをして、以下のようなモデルで$t_*$を予測します。このモデルをNadaraya-Watsonモデルといいます。

$$\begin{aligned} y(\mathbf{x}_*) = \sum^N_{n=1}k(\mathbf{x_*}, \mathbf{x_n})t_n \end{aligned}$$

ここで定義より、$k(\cdot, \cdot)$は以下の2つの条件を満たしています。

$$\begin{aligned} k(\mathbf{x_*}, \mathbf{x_n}) &\geq 0 \\ \sum^N_{n=1}k(\mathbf{x_*}, \mathbf{x_n}) &= 1 \end{aligned}$$

次に、以下のように具体的な$k(\cdot, \cdot)$を定めて、先ほどのデータを用いて予測分布と平均二乗誤差を求めます。必ずしも$g(\cdot)$をガウス分布にする必要はありません。

$$\begin{aligned} k(\mathbf{x_*}, \mathbf{x_n}) = \frac{\mathcal{N}(\mathbf{x}_* | \mathbf{x}_n, \sigma^2)}{\sum^N_{m=1}\mathcal{N}(\mathbf{x}_* | \mathbf{x}_m, \sigma^2)} \\ \end{aligned}$$

$k(\mathbf{x_*}, \mathbf{x_n})$のパラメータ$\sigma$の値によって、どれだけ個々のデータに適合するかが決まります。$\sigma=0.36$となっている右上の図を見てみると、予測分布がなめらかな曲線になっています。

学習と作図コード

def nadaraya_watson(sigma, xs, ts, x_star):
    prob_sum = 0
    tmp_t = 0
    for (x, t) in zip(xs, ts):
        prob = norm.pdf(x_star, x, sigma)
        prob_sum += prob
        tmp_t += prob * t
    pre_t = tmp_t / prob_sum

    return pre_t

sigmas = [(0.1*i) ** 2 for i in range(1, 21)]
nw_RMSEs = []
nadaraya_watson_ts = [[] for _ in range(len(sigmas))]

for (i, sigma) in enumerate(sigmas):
    for x in line_x:
        nadaraya_watson_ts[i].append(nadaraya_watson(sigma, data_x, data_t, x))
    nw_RMSEs.append(RMSE(line_t, nadaraya_watson_ts[i]))

fig = plt.figure(figsize=(12, 9))

ax1 = fig.add_subplot(2, 2, 1)
ax2 = fig.add_subplot(2, 2, 2)
ax3 = fig.add_subplot(2, 2, 3)
ax4 = fig.add_subplot(2, 2, 4)

ax1.scatter(data_x, data_t)
ax1.plot(line_x, line_t)
ax1.plot(line_x, nadaraya_watson_ts[0], label="$\sigma=0.01$")

ax2.scatter(data_x, data_t)
ax2.plot(line_x, line_t)
ax2.plot(line_x, nadaraya_watson_ts[5], label="$\sigma=0.36$")

ax3.scatter(data_x, data_t)
ax3.plot(line_x, line_t)
ax3.plot(line_x, nadaraya_watson_ts[9], label="$\sigma=1.0$")

ax4.scatter(data_x, data_t)
ax4.plot(line_x, line_t)
ax4.plot(line_x, nadaraya_watson_ts[19], label="$\sigma=4.0$")

ax1.legend(loc = 'upper left')
ax2.legend(loc = 'upper left')
ax3.legend(loc = 'upper left')
ax4.legend(loc = 'upper left')

plt.show()

作図コード

plt.plot(sigmas, nw_RMSEs)
plt.xlabel("sigma")
plt.ylabel("RMSE")
plt.show()

理論

モデル

目的変数$t_n$が、$y(\mathbf{z}_n)$にガウス分布に従う誤差が加えられて生成されていると考えます。また、$\mathbf{z}_n$は直接観測できず、何らかの分布$g(\mathbf{\xi}_n)$に従う$\mathbf{\xi}_n$を用いて、$\mathbf{x}_n = \mathbf{z}_n + \mathbf{\xi}_n$の形で観測されると考えます。出力の誤差がガウス分布に従うため、観測値$\{\mathbf{x}_n, t_n\} \; (n = 1, \cdots N)$と対応する2乗和誤差関数を考えます。

$$\begin{align} E = \frac{1}{2}\sum^N_{n=1}\int\{y(\mathbf{x}_n - \mathbf{\xi}_n) - t_n\}^2g(\mathbf{\xi}_n)d\mathbf{\xi}_n \end{align}$$

これを変分法を用いて$E$を$y(\mathbf{z})$に関して最小化することで、$y(\mathbf{x})$の最適解がNadaraya-Watsonモデルで与えられることを示します。

解の導出

まず、$y(\mathbf{x})$の微小変化を考えます。$\epsilon$を十分小さくとり、$\eta(\mathbf{x})$を任意の関数として、

$$\begin{aligned} y(\mathbf{x}) \rightarrow y(\mathbf{x}) + \epsilon\eta(\mathbf{x}) \end{aligned}$$

とします。これを$(1)$の右辺の$y$に代入して、$\tilde{E}$とおくと、

$$\begin{aligned} \tilde{E} &= \frac{1}{2}\sum^N_{n=1}\int\{y(\mathbf{x}_n - \mathbf{\xi}_n) + \epsilon\eta(\mathbf{x}_n - \mathbf{\xi}_n) - t_n\}^2g(\mathbf{\xi}_n)d\mathbf{\xi}_n \\ &= E + \epsilon \cdot \frac{1}{2}\sum^N_{n=1}\int\{y(\mathbf{x}_n - \mathbf{\xi}_n) - t_n\}\eta(\mathbf{x}_n - \mathbf{\xi}_n)g(\mathbf{\xi}_n)d\mathbf{\xi}_n + O(\epsilon^2) \end{aligned}$$

となります。$\epsilon$の係数が$0$になるとき、$E$は最小となるので、$\epsilon$の係数を$0$とおいて、

$$\begin{align} \frac{1}{2}\sum^N_{n=1}\int\{y(\mathbf{x}_n - \mathbf{\xi}_n) - t_n\}\eta(\mathbf{x}_n - \mathbf{\xi}_n)g(\mathbf{\xi}_n)d\mathbf{\xi}_n = 0 \end{align}$$

とします。これは全ての$\eta(\mathbf{x})$に対して成り立つ必要があるので、

$$\begin{aligned} \eta(\mathbf{x}) = \delta(\mathbf{x} - \mathbf{z}) \end{aligned}$$

を選べば良いです。また、こうすることで、$\mathbf{\xi}_n$上の積分を評価できます。

$$\begin{aligned} (2) &\Leftrightarrow \sum^N_{n=1}\int\{y(\mathbf{x}_n - \mathbf{\xi}_n) - t_n\}\delta(\mathbf{x}_n + \mathbf{\xi}_n - \mathbf{z})g(\mathbf{\xi}_n)d\mathbf{\xi}_n = 0 \\ &\Leftrightarrow \sum^N_{n=1}\{y(\mathbf{z}) - t_n\}g(\mathbf{z} - \mathbf{x}_n) = 0 \\ &\Leftrightarrow y(\mathbf{z})\sum^N_{n=1}g(\mathbf{z} - \mathbf{x}_n) = \sum^N_{n=1}t_ng(\mathbf{z} - \mathbf{x}_n) \\ &\Leftrightarrow y(\mathbf{z}) = \sum^N_{n=1}t_n\frac{g(\mathbf{z} - \mathbf{x}_n)}{\sum^N_{m=1}g(\mathbf{z} - \mathbf{x}_m)} \\ \end{aligned}$$

今、$\mathbf{z}$を$\mathbf{x}_*$とすれば、

$$\begin{aligned} y(\mathbf{x}_*) &= k(\mathbf{x}_*, \mathbf{x}_n)t_n \\ where \quad k(\mathbf{x}_*, \mathbf{x}_n) &= \frac{g(\mathbf{x}_* - \mathbf{x}_n)}{\sum^N_{m=1}g(\mathbf{x}_* - \mathbf{x}_m)} \end{aligned}$$

となります。これで、確かに$y(\mathbf{x})$の最適解がNadaraya-Watsonモデルで与えられることが示せました。

この記事では書いていませんが、PRMLの6.3.1では別の方法でNadraya-Watsonモデルを導出しています。そちらでは入力と出力の同時分布を考えた後、入力に関しての条件付き分布の期待値としてNadraya-Watsonモデルが導出されます。最適解だけでなく条件付き分布も導出することでより多くの情報が得られますので、気になった方は読んでみるといいと思います。