ガウス過程によって分類問題を解く

はじめに

PRML(Pattern Recognition and Machine Learning)でガウス過程回帰について学んだ内容をまとめて、実際のデータを使って学習しました。主に6章の内容です。予測分布の導出が個人的に複雑だと思ったので、Step0からStep7に分けて書きました。

ガウス過程分類の予測分布を導出

Step0: 問題設定

N個の既知のデータの組$((\mathbf{x}_1, t_1), ... (\mathbf{x}_N, t_N)), t_i \in \{0, 1\}$があります。今、新しく$\mathbf{x}_{N+1}$を知った時、$t_{N+1}$を予測したいです。つまり、予測分布$p(t_{N+1} | \mathbf{t}_N)$を知りたいです。ここで、$\mathbf{t}_N = (t_1, ... , t_N)^T$です。見やすさのために、条件付きの部分の$\mathbf{x}_1, ... , \mathbf{x}_N, \mathbf{x}_{N+1}$は省略します。また、$t_{N+1} \in \{0, 1\}$より、予測分布を知るには以下を求めれば十分です。

$$\begin{aligned} \tag{0.1} p(t_{N+1}=1 | \mathbf{t}_N) \end{aligned}$$

Step1: 予測分布を知るために

まず、（半）正定値カーネル$k(\cdot, \cdot)$を定めます。そして、ガウス過程に基づいて$\mathbf{a}_{N+1}$の分布を以下のようにします。

$$\tag{1.1} \begin{aligned} p(\mathbf{a}_{N+1}) = \mathcal{N}(\mathbf{a} | \mathbf{0}, \mathbf{C}_{N+1}) \end{aligned}$$

ここで、共分散行列が正定値行列であることを保証するためにノイズのようなパラメータ$\nu$を事前に固定して、$\mathbf{C}_{N+1}$の要素を以下のように表します。

$$\tag{1.2} \begin{aligned} \mathbf{C}_{N+1} &= \begin{pmatrix} \mathbf{C}_N & \mathbf{k} \\ \mathbf{k}^T & c \end{pmatrix} \\ where \quad \mathbf{C}_{Nnm} &= k(\mathbf{x}_n, \mathbf{x}_m) + \nu\delta_{nm} \\ k_n &= k(\mathbf{x}_n, \mathbf{x}_{N+1}) \\ c &= k(\mathbf{x}_{N+1}, \mathbf{x}_{N+1}) + \nu \end{aligned}$$

いま、$t \in {0, 1}$の2値分類を考えています。シグモイド関数$y = \sigma(a)$を用いて関数を変換すると、関数$y(\mathbf{x})$上の非ガウス確率過程$y \in (0, 1)$が得られます。この時、$t$の確率分布はベルヌーイ分布で与えられます。よって、予測分布$(0.1)$は以下のようになります。

$$\tag{1.3} \begin{aligned} p(t_{N+1} = 1|\mathbf{t}_N) &= \int p(t_{N+1} = 1|a_{N+1})p(a_{N+1}|\mathbf{t}_N)da_{N+1} \\ &= \int \sigma(a_{N+1})p(a_{N+1} | \mathbf{t}_N)da_{N+1} \\ \end{aligned}$$

上記の積分は解析的に解けないので、別の方法を考える必要があります。$p(a_{N+1} | \mathbf{t}_N)$をガウス分布で近似できれば、$p(t_{N+1} = 1|\mathbf{t}_N)$を近似的に求めることができます。

Step2: $p(a_{N+1}|\mathbf{t}_N)$をガウス分布で近似するために

$$\tag{2.1} \begin{aligned} p(a_{N+1}|\mathbf{t}_N) &= \int p(a_{N+1}, \mathbf{a}_N|\mathbf{t}_N)d\mathbf{a}_N \\ &= \frac{1}{p(\mathbf{t}_N)} \int p(a_{N+1}, \mathbf{a}_N)p(\mathbf{t}_N | a_{N+1}, \mathbf{a}_N)d\mathbf{a}_N \\ &= \frac{1}{p(\mathbf{t}_N)} \int p(a_{N+1}|\mathbf{a}_N)p(\mathbf{a}_N)p(\mathbf{t}_N|\mathbf{a}_N)d\mathbf{a}_N \\ &= \int p(a_{N+1}|\mathbf{a}_N)p(\mathbf{a}_N|\mathbf{t}_N)d\mathbf{a}_N \end{aligned}$$

条件付き分布$p(a_{N+1}|\mathbf{a}_N)$は、$(1.1), (1.2)$より以下のようになります。

$$\tag{2.2} \begin{aligned} p(a_{N+1}|\mathbf{a}_N) = \mathcal{N}(a_{N+1}|\mathbf{k}^T\mathbf{C}_N^{-1}\mathbf{a}_N, c - \mathbf{k}^T\mathbf{C}_N^{-1}\mathbf{k}) \end{aligned}$$

これより、$p(a_{N+1}|\mathbf{t}_N)$は次のようにかけます。

$$\tag{2.3} \begin{aligned} p(a_{N+1}|\mathbf{t}_N) &= \int p(a_{N+1}, \mathbf{a}_N|\mathbf{t}_N)d\mathbf{a}_N \\ &= \int \mathcal{N}(a_{N+1}|\mathbf{k}^T\mathbf{C}_N^{-1}\mathbf{a}_N, c - \mathbf{k}^T\mathbf{C}_N^{-1}\mathbf{k})p(\mathbf{a}_N|\mathbf{t}_N)d\mathbf{a}_N \end{aligned}$$

よって、$p(\mathbf{a}_N|\mathbf{t}_N)$をガウス分布で近似できれば、$p(a_{N+1}|\mathbf{t}_N)$の近似が求まります。

Step3: $p(\mathbf{a}_N|\mathbf{t}_N)$をガウス分布で近似する

$p(\mathbf{a}_N|\mathbf{t}_N)$をラプラス近似という方法で、ガウス分布で近似します。ラプラス近似には、$p(\mathbf{a}_N|\mathbf{t}_N)$のモードとモードにおけるヘッセ行列が必要です。

$$\tag{3.1} \begin{aligned} p(\mathbf{t}_N|\mathbf{a}_N) &= \prod^N_{n=1}\sigma(a_n)^{t_n}(1 - \sigma(a_n))^{1-t_n} \\ &= \prod^N_{n=1} e^{a_n t_n}\sigma(-a_n) \end{aligned}$$

$$\tag{3.2} \begin{aligned} p(\mathbf{a}_N|\mathbf{t}_N) &= \frac{p(\mathbf{a}_N)p(\mathbf{t}_N|\mathbf{a}_N)}{p(\mathbf{t}_N)} \\ &\propto p(\mathbf{a}_N)p(\mathbf{t}_N|\mathbf{a}_N) \end{aligned}$$

$\Psi(\mathbf{a}_N) = ln(p(\mathbf{a}_N)p(\mathbf{t}_N|\mathbf{a}_N))$とおきます。そうすると、$(1.1), (3.2)$より

$$\tag{3.3} \begin{aligned} \Psi(\mathbf{a}_N) &= lnp(\mathbf{a}_N) + lnp(\mathbf{t}_N|\mathbf{a}_N) \\ &= -\frac{1}{2}\mathbf{a}_N^T\mathbf{C}_N^{-1}\mathbf{a}_N - \frac{N}{2}ln(2\pi) - \frac{1}{2}ln|\mathbf{C}_N| + \mathbf{t}_N^T\mathbf{a}_N - \sum^N_{n=1}ln(1 + e^{a_n}) \end{aligned}$$

となります。$p(\mathbf{a}_N|\mathbf{t}_N)$のモードを見つけたいのですが、そのために$\nabla\Psi(\mathbf{a}_N)$が必要です。

$$\tag{3.4} \begin{aligned} \nabla \Psi(\mathbf{a}_N) = \mathbf{t}_N - \mathbf{\sigma}_N - \mathbf{C}_N^{-1}\mathbf{a}_N \end{aligned}$$

ここで、$\mathbf{\sigma}_N$は$\sigma(a_n)$を要素にもつベクトルです。ここで、$\mathbf{\sigma}_N$は$\mathbf{a}_N$の非線形関数であることより、勾配をゼロにすることでモードを求めることはできないです。なので、Newton-Raphson法によってモードを求めます。それには$\Psi(\mathbf{a}_N)$の2回微分が必要ですが、以下のようになります。

$$\tag{3.5} \begin{aligned} \nabla\nabla\Psi(\mathbf{a}_N) = -\mathbf{W}_N - \mathbf{C}_N^{-1} \end{aligned}$$

ここで、$\mathbf{W}_N$は$\sigma(a_n)(1 - \sigma(a_n))$が対角成分になっている対角行列です。これらの対角成分は$(0, \frac{1}{4})$の範囲にあるため、
$\mathbf{W}_N$は正定値行列です。また、$\mathbf{C}_N$は元から正定値行列であり、二つの正定値行列の和もまた正定値行列であるので、ヘッセ行列$\mathbf{A} = -\nabla\nabla\Psi(\mathbf{a}_N)$は正定値行列です。よって事後分布$lnp(\mathbf{a}_N|\mathbf{t}_N)$は対数凸であり、大域的な最大値である単一のモードを持ちます。Newton-Raphson方程式を用いると、$\mathbf{a}_N$の更新式は次のようになります。

$$\tag{3.6} \begin{aligned} \mathbf{a}_N^{new} &= \mathbf{a}_N - (\nabla\nabla\Psi(\mathbf{a}_N))^{-1}\nabla\Psi(\mathbf{a}_N) \\ &= \mathbf{a}_N - (-\mathbf{W}_N - \mathbf{C}_N^{-1})^{-1}\{\mathbf{t}_N - \mathbf{\sigma}_N - \mathbf{C}_N^{-1}\mathbf{a}_N\} \\ &= \mathbf{a}_N + \mathbf{C}_N(\mathbf{I} + \mathbf{W}_N\mathbf{C}_N)^{-1}\{\mathbf{t}_N - \mathbf{\sigma}_N - \mathbf{C}_N^{-1}\mathbf{a}_N\} \\ &= \mathbf{C}_N(\mathbf{I} + \mathbf{W}_N\mathbf{C}_N)^{-1}\{\mathbf{t}_N - \mathbf{\sigma}_N + (\mathbf{I} + \mathbf{W}_N\mathbf{C}_N)\mathbf{C}_N^{-1}\mathbf{a}_N - \mathbf{C}_N^{-1}\mathbf{a}_N\} \\ &= \mathbf{C}_N(\mathbf{I} + \mathbf{W}_N\mathbf{C}_N)^{-1}\{\mathbf{t}_N - \mathbf{\sigma_N} + \mathbf{W}_N\mathbf{a}_N\} \end{aligned}$$

この更新は$\mathbf{a}_N$がモード$\mathbf{a}_N^*$に収束するまで繰り返します。モードでは、勾配$\Psi(\mathbf{a}_N)$は0となるので、$(3.4)$より$\mathbf{a}_N^*$について下記の式が成り立ちます。

$$\tag{3.7} \begin{aligned} \mathbf{a}_N^* = \mathbf{C}_N(\mathbf{t}_N - \mathbf{\sigma_N}) \end{aligned}$$

いま、事後分布のモード$\mathbf{a}_N^*$を用いてヘッセ行列を評価したものを$\mathbf{H}$とおくと、

$$\tag{3.8} \begin{aligned} \mathbf{H} = \mathbf{W}_N + \mathbf{C}_N^{-1} \end{aligned}$$

となります。ここで、$\mathbf{W}_N$は$\mathbf{a}_N^*$で評価しています。以上より、事後分布$p(\mathbf{a}_N|\mathbf{t}_N)$のモードとモードにおけるヘッセ行列が求まりました。よってラプラス近似によって、$p(\mathbf{a}_N|\mathbf{t}_N)$の正規分布による近似$q(\mathbf{a}_N)$が以下のように求まります。

$$\tag{3.9} \begin{aligned} q(\mathbf{a}_N) = \mathcal{N}(\mathbf{a}_N | \mathbf{a}_N^*, \mathbf{H}^{-1}) \end{aligned}$$

Step4: $p(a_{N+1} | \mathbf{t}_N)$をガウス分布によって近似する

$(2.3), (3.9)$より、以下のようになります。

$$\tag{4.1} \begin{aligned} p(a_{N+1}|\mathbf{t}_N) &= \int \mathcal{N}(a_{N+1}|\mathbf{k}^T\mathbf{C}_N^{-1}\mathbf{a}_N, c - \mathbf{k}^T\mathbf{C}_N^{-1}\mathbf{k})p(\mathbf{a}_N|\mathbf{t}_N)d\mathbf{a}_N \\ &\simeq \int \mathcal{N}(a_{N+1}|\mathbf{k}^T\mathbf{C}_N^{-1}\mathbf{a}_N, c - \mathbf{k}^T\mathbf{C}_N^{-1}\mathbf{k})\mathcal{N}(\mathbf{a}_N | \mathbf{a}_N^*, \mathbf{H}^{-1}) \\ &= \mathcal{N}(\mathbf{k}^T(\mathbf{t}_N - \mathbf{\sigma_N}), c - \mathbf{k}^T(\mathbf{W}_N^{-1} + \mathbf{C}_N)^{-1}\mathbf{k}) \\ &= \mathcal{N}(\mu, \sigma^2) \\ where \quad \mu &= \mathbf{k}^T(\mathbf{t}_N - \mathbf{\sigma_N}) \\ \sigma^2 &= c - \mathbf{k}^T(\mathbf{W}_N^{-1} + \mathbf{C}_N)^{-1}\mathbf{k} \end{aligned}$$

Step5: $\sigma(a_{N+1})$を近似する

$(1.3), (4.1)$より、次のようになります。

$$\tag{5.1} \begin{aligned} p(t_{N+1} = 1|\mathbf{t}_N) &= \int \sigma(a_{N+1})p(a_{N+1} | \mathbf{t}_N)da_{N+1} \\ &\simeq \int \sigma(a_{N+1}\mathcal{N}(\mu, \sigma^2)da_{N+1} \end{aligned}$$

この積分を解析的に求めることは困難なので、次のプロビット関数$\Phi(a)$を考えます。これを用いてシグモイド関数を近似することを考えます。

$$\tag{5.2} \begin{aligned} \Phi(a) = \int^a_{-\infin} \mathcal{N}(\theta | 0, 1)d\theta \end{aligned}$$

そして、$\Phi(\lambda a)$用いて、シグモイド関数$\sigma(a)$を近似することを考えます。原点において二つの関数の微分が等しくなるような$\lambda$を考えます。まず、$\sigma(a)$の原点における微分は、

$$\tag{5.3} \begin{aligned} \left.\frac{d\sigma(a)}{da}\right|_{a=0} &= \left.\frac{e^{-a}}{(1 + e^{-a})^2}\right|_{a=0} \\ &= \frac{1}{4} \end{aligned}$$

また、$\Phi(\lambda a)$の原点における微分は、

$$\tag{5.4} \begin{aligned} \left.\frac{d\Phi(\lambda a)}{da}\right|_{a=0} &= \left.\frac{d\Phi(\lambda a)}{d(\lambda a)}\frac{d\lambda a}{da}\right|_{a=0} \\ &= \left.\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}\lambda^2a^2}\lambda\right|_{a=0} \\ &= \frac{\lambda}{\sqrt{2\pi}} \end{aligned}$$

$(5.3), (5.4)$より、

$$\tag{5.5} \begin{aligned} \frac{1}{4} &= \frac{\lambda}{\sqrt{2\pi}} \\ \Leftrightarrow \lambda &= \frac{\sqrt{2\pi}}{4} \end{aligned}$$

となるので、以下のようになります。

$$\tag{5.6} \begin{aligned} \sigma(a) \simeq \Phi(\frac{\sqrt{2\pi}}{4}a) \end{aligned}$$

また、2つの関数を以下に描画しました。

pythonの描画コード

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm


def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def lambda_probit(lam, x):
    return norm.cdf(x, loc=0, scale=1/lam)

xs = np.linspace(-5, 5, 1000)
plt.plot(xs, sigmoid(xs), label="sigmoid")
plt.plot(xs, lambda_probit(np.sqrt(2 * np.pi) / 4, xs), label="lambda_probit")
plt.legend()

これを用いて、$p(t_{N+1} = 1|\mathbf{t}_N)$は次のように書けます。

$$\tag{5.7} \begin{aligned} p(t_{N+1} = 1|\mathbf{t}_N) &\simeq \int \sigma(a_{N+1})\mathcal{N}(\mu, \sigma^2)da_{N+1} \\ &\simeq \int \Phi(\frac{\sqrt{2\pi}}{4} a_{N+1})\mathcal{N}(\mu, \sigma^2)da_{N+1} \\ \end{aligned}$$

Step6: $\int \Phi(\frac{\sqrt{2\pi}}{4} a_{N+1})\mathcal{N}(\mu, \sigma^2)da_{N+1}$を求める

まず、$X \sim \mathcal{N}(0, \frac{8}{\pi}), Y \sim \mathcal{N}(\mu, \sigma)$で$X$と$Y$は互いに独立とします。そうすると、$X - Y \sim \mathcal{N}(-\mu, \lambda^{-2} + \sigma^2)$より、

$$\tag{6.1} \begin{aligned} \int \Phi(\frac{\sqrt{2\pi}}{4} a_{N+1})\mathcal{N}(\mu, \sigma^2)da_{N+1} &= \int P(X \leq a_{N+1})P(Y = a_{N+1})da_{N+1} \\ &= \int P(X \leq Y | Y = a_{N+1})P(Y = a_{N+1})da_{N+1} \\ &= \int P(X \leq Y) \\ &= P(X - Y \leq 0) \\ &= \Phi\left(\frac{0 - (-\mu)}{\sqrt{\frac{8}{\pi} + \sigma^2}}\right) \\ &= \Phi\left(\frac{\mu}{\sqrt{\frac{8}{\pi} + \sigma^2}}\right) \end{aligned}$$

となります。

$(5.6), (6.1)$より、

$$\tag{6.2} \begin{aligned} p(t_{N+1} = 1|\mathbf{t}_N) &\simeq \Phi\left(\frac{\mu}{\sqrt{\frac{8}{\pi} + \sigma^2}}\right) \end{aligned}$$

となります。

Step7: $\Phi\left(\frac{\mu}{\sqrt{\frac{8}{\pi} + \sigma^2}}\right)$を近似する

$(5.6), (6.2)$より、以下のようになります。

$$\tag{7.1} \begin{aligned} p(t_{N+1} = 1|\mathbf{t}_N) &\simeq \Phi\left(\frac{\mu}{\sqrt{\frac{8}{\pi} + \sigma^2}}\right) \\ &\simeq \sigma\left(\frac{\mu}{\frac{\sqrt{2\pi}}{4}\sqrt{\frac{8}{\pi} + \sigma^2}}\right) \\ &= \sigma\left(\frac{\mu}{\sqrt{1 + \frac{\pi}{8}\sigma^2}}\right) \end{aligned}$$

まとめ

この式は右にスライドできます

$$\begin{aligned} &p(t_{N+1} = 1|\mathbf{t}_N) &(\because Step0) \\ =& \int \sigma(a_{N+1})p(a_{N+1} | \mathbf{t}_N)da_{N+1} &(\because Step1) \\ =& \int \sigma(a_{N+1})\int \mathcal{N}(a_{N+1}|\mathbf{k}^T\mathbf{C}_N^{-1}\mathbf{a}_N, c - \mathbf{k}^T\mathbf{C}_N^{-1}\mathbf{k})p(\mathbf{a}_N|\mathbf{t}_N)d\mathbf{a}_Nda_{N+1} &(\because Step2) \\ \simeq& \int \sigma(a_{N+1})\int \mathcal{N}(a_{N+1}|\mathbf{k}^T\mathbf{C}_N^{-1}\mathbf{a}_N, c - \mathbf{k}^T\mathbf{C}_N^{-1}\mathbf{k})\mathcal{N}(\mathbf{a}_N | \mathbf{a}_N^*, \mathbf{H}^{-1})d\mathbf{a}_Nda_{N+1} &(\because Step3) \\ =& \int \sigma(a_{N+1})\mathcal{N}(\mathbf{k}^T(\mathbf{t}_N - \mathbf{\sigma_N}), c - \mathbf{k}^T(\mathbf{W}_N^{-1} + \mathbf{C}_N)^{-1}\mathbf{k})da_{N+1} &(\because Step4) \\ \simeq& \int \Phi(\frac{\sqrt{2\pi}}{4}a)\mathcal{N}(\mathbf{k}^T(\mathbf{t}_N - \mathbf{\sigma_N}), c - \mathbf{k}^T(\mathbf{W}_N^{-1} + \mathbf{C}_N)^{-1}\mathbf{k})da_{N+1} &(\because Step5) \\ =& \Phi\left(\frac{\mathbf{k}^T(\mathbf{t}_N - \mathbf{\sigma_N})}{\sqrt{\frac{8}{\pi} + (c - \mathbf{k}^T(\mathbf{W}_N^{-1} + \mathbf{C}_N)^{-1}\mathbf{k}})}\right) &(\because Step6) \\ \simeq& \sigma\left(\frac{\mathbf{k}^T(\mathbf{t}_N - \mathbf{\sigma_N})}{\sqrt{1 + \frac{\pi}{8}(c - \mathbf{k}^T(\mathbf{W}_N^{-1} + \mathbf{C}_N)^{-1}\mathbf{k}})}\right) &(\because Step7) \\ \end{aligned}$$

パラメータの最適化

カーネル$k(\cdot, \cdot)$を決まった関数ではなくパラメータ$\mathbf{\theta}$をもったものとして、その$\mathbf{\theta}$を最適化することを考えます。事後分布$p(\mathbf{\theta} | \mathbf{t}_N)$は以下のようになります。

$$\begin{aligned} p(\mathbf{\theta} | \mathbf{t}_N) &\propto p(\mathbf{\theta})p(\mathbf{\mathbf{t}_N} | \mathbf{\theta}) \\ \end{aligned}$$

事前分布$p(\mathbf{\theta})$は、適当に設定すればよいので、尤度関数$p(\mathbf{\mathbf{t}_N} | \mathbf{\theta})$について考えます。（例えば$p(\mathbf{\theta}) = \mathcal{N}(\mathbf{0}, \alpha^{-1}\mathbf{I})$のようにします）

尤度関数のモードを求めることは困難です。なので、対数尤度関数の勾配$\frac{\partial lnp(\mathbf{t}_N|\mathbf{\theta})}{\partial \mathbf{\theta}}$を求めて、それを用いて標準的な非線形の最適化アルゴリズムによって最適解に近い解を求めることを目標にします。

$\frac{\partial \Psi(\mathbf{a}_N^*)}{\partial \mathbf{a}_N} = 0$であるので、以下のようになります。

$$\tag{A.1} \begin{aligned} \frac{\partial lnp(\mathbf{t}_N | \mathbf{\theta})}{\partial \theta_j} = -\frac{1}{2}\sum^N_{n=1}\frac{\partial ln|\mathbf{W}_N + \mathbf{C}_N^{-1}|}{\partial a_n^*}\frac{\partial a_n^*}{\partial \theta_j} \\ \end{aligned}$$

ここで、

$$\tag{A.2} \begin{aligned} \frac{\partial ln|\mathbf{W}_N + \mathbf{C}_N^{-1}|}{\partial a_n^*} &= Tr\left[(\mathbf{W}_N + \mathbf{C}_N^{-1})^{-1}\frac{\partial\mathbf{W}_N}{\partial\mathbf{a}_N^*}\right] \\ &= Tr\left[(\mathbf{C}_N^{-1}(\mathbf{I} + \mathbf{C}_N\mathbf{W}_N))^{-1}\frac{\partial\mathbf{W}_N}{\partial\mathbf{a}_N^*}\right] \\ &= [(\mathbf{I} + \mathbf{C}_N\mathbf{W}_N)^{-1}\mathbf{C}_N]_{nn}\frac{\partial}{\partial a_n^*}\sigma(a_n^*)(1 - \sigma(a_n^*)) \\ &= [(\mathbf{I} + \mathbf{C}_N\mathbf{W}_N)^{-1}\mathbf{C}_N]_{nn}\sigma(a_n^*)(1 - \sigma(a_n^*))(1 - 2\sigma(a_n^*)) \end{aligned}$$

となるので、対数尤度関数の微分は以下のようになります。

$$\tag{A.3} \begin{aligned} \frac{\partial lnp(\mathbf{t}_N | \mathbf{\theta})}{\partial \theta_j} = -\frac{1}{2}\sum^N_{n=1}[(\mathbf{I} + \mathbf{C}_N\mathbf{W}_N)^{-1}\mathbf{C}_N]_{nn}\sigma(a_n^*)(1 - \sigma(a_n^*))(1 - 2\sigma(a_n^*))\frac{\partial a_n^*}{\partial \theta_j} \end{aligned}$$

今、$\frac{\partial \mathbf{a}_N^*}{\partial \theta_j}$を考えて、

$$\tag{A.4} \begin{aligned} \frac{\partial \mathbf{a}_N^*}{\partial \theta_j} &= \frac{\partial}{\partial \theta_j}(\mathbf{C}_N(\mathbf{t}_N - \mathbf{\sigma}_N)) \\ &= \frac{\partial \mathbf{C}_N}{\partial \theta_j}(\mathbf{t}_N - \mathbf{\sigma}_N) - \mathbf{C}_N\frac{\partial \mathbf{\sigma}_N}{\partial \theta_j} \end{aligned}$$

ここで、

$$\tag{A.5} \begin{aligned} \frac{\partial \mathbf{\sigma}_N}{\partial \theta_j} &= \frac{\partial \mathbf{\sigma}_N}{\partial \mathbf{a}_N^*}\frac{\partial \mathbf{a}_N^*}{\partial \theta_j} \\ &= \begin{pmatrix} \frac{\partial \sigma(a_1^*)}{\partial a_1^*} & & \text{\huge{0}} \\ & \ddots & \\ \text{\huge{0}} & & \frac{\partial \sigma(a_N^*)}{\partial a_N^*} \\ \end{pmatrix} \frac{\partial \mathbf{a}_N^*}{\partial \theta_j} \\ &= \begin{pmatrix} \sigma(a_1^*)(1 - \sigma(a_1^*)) & & \text{\huge{0}} \\ & \ddots & \\ \text{\huge{0}} & & \sigma(a_N^*)(1 - \sigma(a_N^*)) \\ \end{pmatrix} \frac{\partial \mathbf{a}_N^*}{\partial \theta_j} \\ &= \mathbf{W}_N\frac{\partial \mathbf{a}_N^*}{\partial \theta_j} \end{aligned}$$

これより、

$$\tag{A.6} \begin{aligned} &\frac{\partial \mathbf{a}_N^*}{\partial \theta_j} = \frac{\partial \mathbf{C}_N}{\partial \theta_j}(\mathbf{t}_N - \mathbf{\sigma}_N) - \mathbf{C}_N\mathbf{W}_N\frac{\partial \mathbf{a}_N^*}{\partial \theta_j} \\ \Leftrightarrow& (\mathbf{I} + \mathbf{C}_N\mathbf{W}_N)\frac{\partial \mathbf{a}_N^*}{\partial \theta_j} = \frac{\partial \mathbf{C}_N}{\partial \theta_j}(\mathbf{t}_N - \mathbf{\sigma}_N) \\ \Leftrightarrow& \frac{\partial \mathbf{a}_N^*}{\partial \theta_j} = (\mathbf{I} + \mathbf{C}_N\mathbf{W}_N)^{-1}\frac{\partial \mathbf{C}_N}{\partial \theta_j}(\mathbf{t}_N - \mathbf{\sigma}_N) \end{aligned}$$

であるので、これと$(A.3)$より対数尤度関数の微分が求まりました。

トイデータで学習

ガウス過程回帰を用いて、2種類のあやめの分類問題に取り組みました。

pythonの学習コード

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split
import seaborn as sns

iris_df_vanilla = sns.load_dataset('iris')
iris_df = iris_df_vanilla[50:]

t_df = iris_df.loc[:, 'species']
t_df = t_df.replace({'versicolor': 1, 'virginica': 0})
x_df = iris_df.loc[:, ['sepal_length', 'sepal_width']]
x_df = (x_df - x_df.mean()) / x_df.std()

N = 50
train_x = x_df[::2].to_numpy(copy=True)
train_t = t_df[::2].to_numpy(copy=True)
test_x = x_df[1::2].to_numpy(copy=True)
test_t = t_df[1::2].to_numpy(copy=True)

def sigmoid(a):
    return 1 / (1 + np.exp(-a))

def diff_C_by_theta(thetas, n):
    thetas = thetas
    num = n

    def closure(x1, x2):
        if num == 0:
            return np.exp(-thetas[1] / 2 * np.dot(x1 - x2, x1 - x2))
        elif num == 1:
            return thetas[0] * np.exp(-1 / 2 * np.dot(x1 - x2, x1 - x2))
        elif num == 2:
            return 1
        elif num == 3:
            return np.dot(x1, x2)
        else:
            raise ValueError()

    return closure

def kernel(thetas, x1, x2):
    return thetas[0] * np.exp(-thetas[1] / 2 * np.dot(x1 - x2, x1 - x2)) + thetas[2] + thetas[3]*np.dot(x1, x2)

def calc_C(thetas, nu=1e-6):
    C = np.zeros((N, N))
    for i in range(N):
        for j in range(N):
            C[i, j] = kernel(thetas, train_x[i], train_x[j]) + nu * (i == j)
    return C

def calc_a_star(C):
    before_a = np.zeros(N)
    a = np.zeros(N)
    I = np.identity(N)
    for iter in range(50):
        tmp_sigma = np.array([sigmoid(an) for an in a])
        tmp_W = np.zeros((N, N))
        for i in range(N):
            tmp_W[i, i] = sigmoid(a[i]) * (1 - sigmoid(a[i]))
        tmp_matrix = np.dot(C, np.linalg.inv(I + np.dot(tmp_W, C)))
        before_a = a
        a = np.dot(tmp_matrix, train_t - tmp_sigma + np.dot(tmp_W, a))
        if sum(abs(a - before_a)) < 1e-10:
            break

    assert sum(abs(a - before_a)) < 1e-8, f"a_starの値が収束していません\n a_dif: {a - before_a}"
    if sum(abs(a - before_a)) > 1e-10:
        print("a_starはあまり収束していません")

    return a

def calc_sigma(a_star):
    sigma = np.array([sigmoid(an) for an in a_star])

    return sigma

def calc_W(thetas, a_star):
    W = np.zeros((N, N))
    for i in range(N):
        W[i, i] = sigmoid(a_star[i]) * (1 - sigmoid(a_star[i]))

    return W

def calc_da_dthetas(thetas, C, a_star, W):
    dC_nn_dtheta = np.zeros((len(thetas), N, N))
    for i in range(len(thetas)):
        diff = diff_C_by_theta(thetas, i)
        for j in range(N):
            for k in range(N):
                dC_nn_dtheta[i][j][k] = diff(train_x[j], train_x[k])
    tmp = np.linalg.inv(np.identity(N) + np.dot(W, C))
    sigma_n = np.array([sigmoid(a) for a in a_star])
    da_dthetas = np.zeros((4, N))
    for i in range(4):
        da_dthetas[i] = np.dot(np.dot(tmp, dC_nn_dtheta[i]), train_t - sigma_n)
    
    return da_dthetas

def diff_log_likelihood(thetas):
    C = calc_C(thetas)
    a_star = calc_a_star(C)
    sigma = calc_sigma(a_star)
    W = calc_W(thetas, a_star)
    da_dthetas = calc_da_dthetas(thetas, C, a_star, W)
    I = np.identity(N)
    dlog_likelihood = np.zeros(len(thetas))
    tmp_matrix = np.dot(np.linalg.inv(I + np.dot(C, W)), C)
    for i in range(len(thetas)):
        for n in range(N):
            dlog_likelihood[i] += -1/2 * tmp_matrix[n, n] * sigma[n] * (1 - sigma[n]) * (1 - 2*sigma[n]) * da_dthetas[i, n]

    return dlog_likelihood

def expect(thetas, C, x_star, a_star, W):
    k = np.array([kernel(thetas, x, x_star) for x in train_x])

    def E(a_star):
        sigma = np.array([sigmoid(a) for a in a_star])
    
        return np.dot(k, train_t - sigma)

    def var(thetas, C, x_star, W):
        c = kernel(thetas, x_star, x_star)
        tmp = np.linalg.inv(np.linalg.inv(W) + C)
        return c - np.dot(np.dot(k.T, tmp), k)

    mu = E(a_star)
    sigma2 = var(thetas, C, x_star, W)
    
    return sigmoid(mu / np.sqrt(1 + np.pi / 8 * sigma2))

def calc_cross_entropy_error(thetas, train_flg=False):
    C = calc_C(thetas)
    a_star = calc_a_star(C)
    W = calc_W(thetas, a_star)
    cross_entropy_error = 0
    if train_flg:
        for (x, true_t) in zip(train_x, train_t):
            expected_t = expect(thetas, C, x, a_star, W)
            cross_entropy_error += -true_t * np.log(sigmoid(expected_t))
    else:
        for (x, true_t) in zip(test_x, test_t):
            expected_t = expect(thetas, C, x, a_star, W)
            cross_entropy_error += -true_t * np.log(sigmoid(expected_t))

    return cross_entropy_error

def Momentum(shape, lr=0.1, momentum=0.99):
    momentum = momentum
    v = np.zeros(shape)

    def closure(grads):
        nonlocal v
        v = momentum*v + lr*grads

        return v

    return closure

alphas = [0.05, 0.06, 0.07, 0.08, 0.09, 0.10]
thetas_by_alphas = np.empty((len(alphas), 4))
for (i, alpha) in enumerate(alphas):
    thetas = np.ones(4)
    momentum = Momentum(thetas.shape)
    for iter in range(1000):
        dlog_likelihood = diff_log_likelihood(thetas)
        dlog_prior_theta = -alpha / 2 * thetas
        dlog_posterior = dlog_likelihood + dlog_prior_theta
        thetas += momentum(dlog_posterior)
        thetas = np.array([max(t, 0) for t in thetas])
        if sum(abs(dlog_posterior)) < 1e-10:
            print(f"iter: {iter+1}, gradient: {dlog_posterior} and break")
            break
        if (iter+1) % 100 == 0:
            print(f"iter: {iter+1}, gradient: {dlog_posterior}, thetas: {thetas}")
    
    thetas_by_alphas[i] = thetas
    train_cross_entropy_error = calc_cross_entropy_error(thetas, train_flg=True)
    test_cross_entropy_error = calc_cross_entropy_error(thetas)
    print(f"alpha: {alpha:.5f}, thetas: {thetas}, train_error: {train_cross_entropy_error:.3f}, test_error: {test_cross_entropy_error:.3f}")
    print()

x1_line = np.linspace(-3, 3, 61).reshape(-1, 1)
x2_line = np.linspace(-3, 3, 61).reshape(-1, 1)
x1_grid, x2_grid = np.meshgrid(x1_line, x2_line)
ps = np.zeros((61, 61))

thetas = thetas_by_alphas[4]

C = calc_C(thetas)
a_star = calc_a_star(C)
W = calc_W(thetas, a_star)
for (i, x1) in enumerate(x1_line):
    for (j, x2) in enumerate(x2_line):
        x_star = np.array([x1[0], x2[0]])
        ps[j, i] = expect(thetas, C, x_star, a_star, W)

plt.scatter(train_x[:25, 0], train_x[:25, 1], label='versicolor')
plt.scatter(train_x[25:, 0], train_x[25:, 1], label='virginica')
plt.xlabel('sepal_width')
plt.ylabel('petal_width')
plt.contour(x1_grid, x2_grid, ps, levels=[0.25, 0.375, 0.5, 0.625, 0.75])
plt.colorbar()
plt.legend()

plt.scatter(test_x[:25, 0], test_x[:25, 1], label='versicolor')
plt.scatter(test_x[25:, 0], test_x[25:, 1], label='virginica')
plt.xlabel('sepal_width')
plt.ylabel('petal_width')
plt.contour(x1_grid, x2_grid, ps, levels=[0.25, 0.375, 0.5, 0.625, 0.75])
plt.colorbar()
plt.legend()

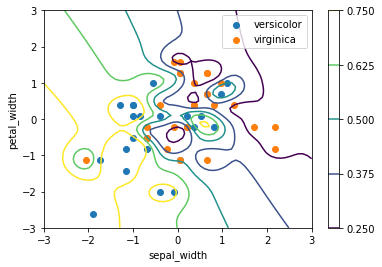
予測を等高線で表しています。数字が大きい方は青色のデータである可能性が高いと予測しています。一枚目の画像は訓練データを、二枚目の画像はテストデータを点で表示しています。