🌈

RGB -> HSV 変換式を中学数学でガチ導出する

2022/10/24に公開

CSS

デザイン

JavaScript

tech

趣味でCSSコードジェネレータ的なサイトをつくろうとしている現在。
どうせなら勉強がてらジェネレータのControl UIをフルスクラッチで自作したいなと思い、その一環でMediumのチュートリアルを参考に、Color Picker Componentをつくり始めたのだが…

HSV、何もわからん。

公式をそのまま覚えるのもなんかちょっと気持ち悪いので、頑張って理解する。

以後、次のように定義する。

const Imax = Math.max(r, g, b)
const Imin = Math.min(r, g, b)

色相H・彩度S・明度V・透明度Aの変化比較

まずは各値が何を制御する値なのか、について図でざっくりと。

明度（どれくらい明るいか）

明度(Value・Brightness)は色の明るさです。
色の明るさを変更するには、RGBの各色の割合を保ったままに、それぞれの値を等倍することで行なえます。

ここでいう明暗は、白に近いか黒に近いか、ということ。

MAX明るい ...rgb(255, 255, 255)
MAX暗い ...rgb(0, 0, 0)

つまり明度とは、

rgbの中で最も主張している色が、どれだけ黒に近いか

すなわち、

rgbの最大値が、0 ~ 255の間のどのあたりにあるか

を表す割合として、式に起こすことができる。

\begin{align*} V &= \cfrac{Imax}{(255 - 0)} \\\\ &= \cfrac{Imax}{255} \end{align*}

パーセント表示にするなら、その割合に100をかけて考える。

\begin{align*} V[\%] &= \cfrac{Imax}{255} \times 100 \\\\ &= \cfrac{Imax \times 100}{255} \\\\ &= \cfrac{Imax \times 100 \times \cfrac{1}{100}}{255 \times \cfrac{1}{100}} \\\\ &= \cfrac{Imax}{2.55} \end{align*}

彩度（どれくらい鮮やかか）

彩度(Saturation・Chroma)は色の鮮やかさです。
色の鮮やかさを変更するには、RGBのうち最も大きなものはそのままに他の値を等倍することで行なえます。

彩度とは、最も主張している色以外をどれだけ薄めるかであり、
R, G, Bの最大値は固定とするので、その他の値を小さくすればするほど、R, G, Bの値はかけ離れたものになっていく。

つまり、彩度とはR,G,Bの値にどれだけ開きがあるかを示す数値だという解釈もできる。

R,G,Bの値に開きが無い場合は、グレーに近い事から、彩度は如何にグレーっぽく無いか？、という事から、どれだけ純色（赤、緑、青、黄、シアン、紫など）に近いか？を表しています。

あくまでも割合で考えたいので、Imaxを1とした時、rgbの幅はどれくらいといえるかを彩度Sとする。

$Imax - Imin$ がrgb値の幅であるので、

S : 1 = (Imax - Imin) : Imax

外側の数値同士の積と内側の数値同士の積は等しいことから、

1 \cdot (Imax - Imin) = S \cdot Imax

S = \cfrac{Imax - Imin}{Imax}

パーセントで表すなら、

S[\%] = \cfrac{Imax - Imin}{Imax} \times 100

もっと解釈 ~ rgbがすべて等しい場合 ~

$r = g = b$ である時、 $Imax = Imin$ であるので、彩度Sは0になる。

S = \cfrac{0}{Imax} = 0

$r = g = b$ であることから、RedもGreenもBlueも均等に混ざり合って、グレー系の色になる。

どの色にもカテゴライズできないグレースケールな色が、彩度0の状態である。

もっと解釈 ~ rgbのいずれかが0の場合 ~

この時、 $Imin = 0$ であるので、彩度Sは1になる。

S = \cfrac{Imax - 0}{Imax} = 1

いずれかの色が完敗しているため、0でない色が鮮やかに主張する。

色相（色の種類）

色の種類を変更するには、RGBのうち最大値と最小値を保ったまま、最大値と最小値の間でrgb各値を変化させることで行なえます。

ここまでで導いた公式からわかるように、 $Imax$ と $Imin$ が変わると、明度や彩度が変わってしまう。
それらを変えずにRGB値を微調整することで、さらに色を変化させることができる。

色相環から規則性を見い出す

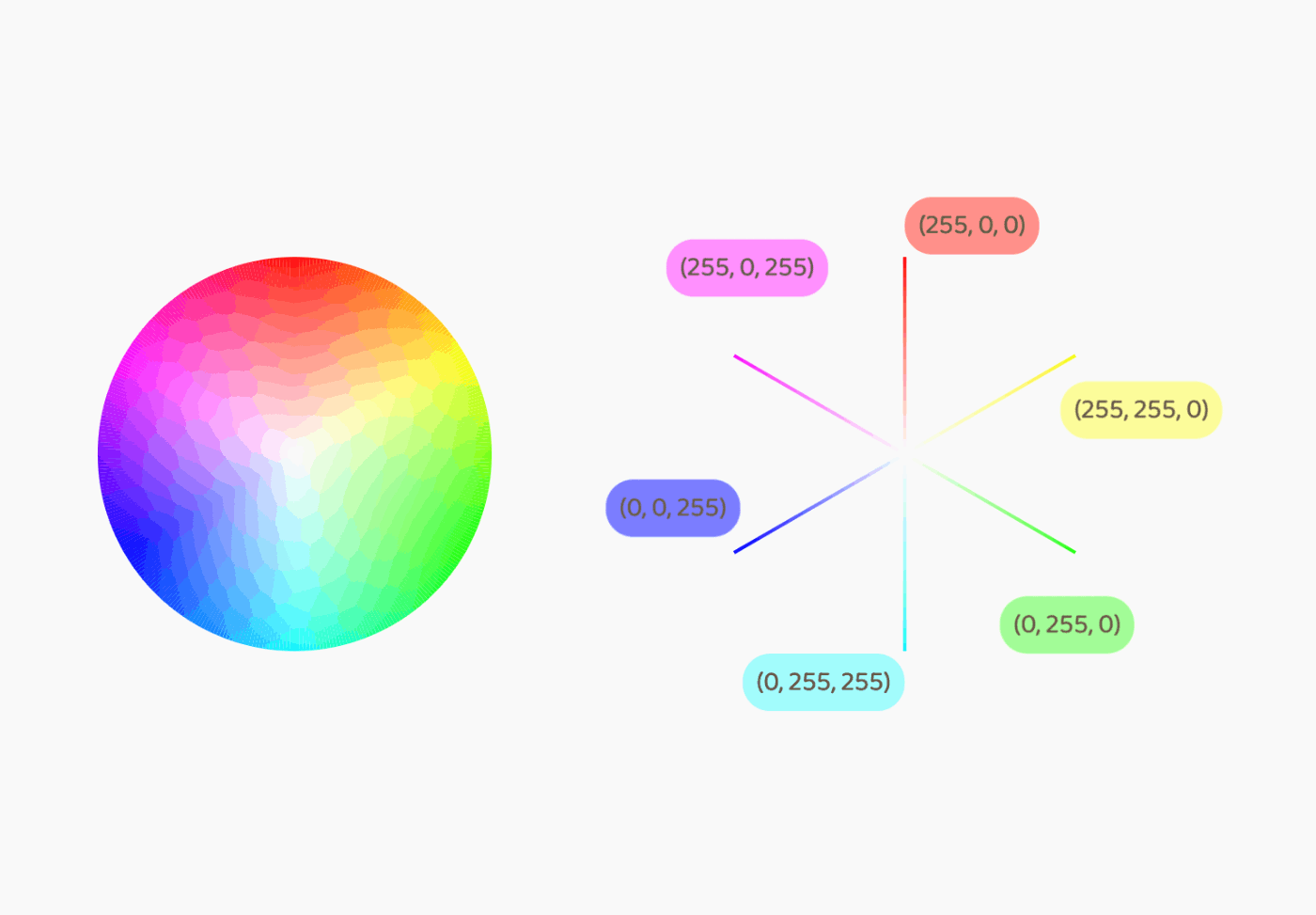
赤色を指すrgb(255, 0, 0)の位置を0°として、そこから時計回りに色を追っていくと、次のような順序で色が変化していくのがわかる。

GをMAXまで増やしていく（赤~黄)
GがMAXになったら、Rを減らしていく(黄~緑)
BをMAXまで増やしていく(緑~水色)
BがMAXになったら、Gを減らしていく(水色~青)
Gが0になったら、Rを増やしていく(青~ピンク)
RがMAXになったら、Bを減らしていく(ピンク~赤)

各区間内での進み具合を求める

色相Hはどのくらい回ればその色を指すようになるかを表す角度である。

色相を求める式の導出に向けて、60°ずつの区間に分けて考えていく。

60°の区間内でどれくらい回転しているか？という割合Xを求め、それを60°にかけてあげれば、区間内で何度回転したかが求まる。

区間内回転角\Theta = 60° \times X

最終的には、区間内回転角 $\Theta$ に、区間の開始角（その区間に突入するまでの回転角）を加えることで、円全体でみた実際の回転角（色相）が求まることになる。

まずはXを考えていこう。

(1) 0°~60°の区間

R = Imax
G = Imin -> Imax
B = Imin < G

この区間内でのGの可動域は $Imax - Imin$ であり、Gを大きくしていく（回転角が大きくなる）につれ、GとBの差が大きくなっていく。

つまり、現在のGとBの差が可動域のどれくらいに達しているかで、進み具合Xが表せるといえる。

X = \cfrac{G - B}{Imax - Imin}

ということでHは、

H = 60° \times \cfrac{G - B}{Imax - Imin}

(2) 60°~120°の区間

R = Imax -> Imin
G = Imax
B = Imin < R

Rの可動域は $Imax - Imin$ であり、Rを小さくしていく（回転角が大きくなる）につれ、BとRの差が小さくなっていく。

つまり、現在のRとBの差が可動域のどれくらいに達しているかで、区間内での進み具合Xが表せる。

X = \cfrac{R - B}{Imax - Imin}

(3) 120°~180°の区間

R = Imin < B
G = Imax
B = Imin -> Imax

X = \cfrac{B - R}{Imax - Imin}

(4) 180°~240°の区間

R = Imin < G
G = Imax -> Imin
B = Imax

X = \cfrac{G - R}{Imax - Imin}

(5) 240°~300°の区間

R = Imin -> Imax
G = Imin < R
B = Imax

X = \cfrac{R - G}{Imax - Imin}

(6) 300°~360°の区間

R = Imax
G = Imin < B
B = Imax -> Imin

X = \cfrac{B - G}{Imax - Imin}

色相を求める式にまとめる

Imax	区間内回転率X	区間の開始角	区間の終了角
R	$- \cfrac{G - B}{Imax - Imin}$	300°	0°（360°)
R	$\cfrac{G - B}{Imax - Imin}$	0°（360°)	60°
G	$- \cfrac{B - R}{Imax - Imin}$	60°	120°
G	$\cfrac{B - R}{Imax - Imin}$	120°	180°
B	$- \cfrac{R - G}{Imax - Imin}$	180°	240°
B	$\cfrac{R - G}{Imax - Imin}$	240°	300°

色相Hはどのくらい回ればその色を指すようになるかを表す角度である。

60°の区間の中でどれくらいの角度まで進んでいるか？という割合Xを求め、それを60°にかけてあげれば、区間内で何度回転したかが求まる。

区間内回転角\Theta = 60° \times X

区間内の回転角に、その区間に到達するまでの回転角も加えることで、色相（実際の回転角）が求められる。

Xにマイナスがついている場合は、区間の終了角から、区間内回転角分戻る（引き算する）と考えると、実はImaxごとに色相を求める式が同一になる。

色相H = \begin{cases} 区間の開始角 + \Theta &\text{(Xが符号なしの場合) } \\ 区間の終了角 - \Theta &\text{(Xにマイナスがついている場合) } \end{cases}

Imax = G の場合

60°~120°

\begin{align*} 色相H &= 120° - (- \cfrac{B - R}{Imax - Imin} \times 60°) \\\\ &= 120° + \cfrac{B - R}{Imax - Imin} \times 60° \end{align*}

120°~180°

\begin{align*} 色相H &= 120° + \cfrac{B - R}{Imax - Imin} \times 60° \end{align*}

Imax = B の場合

180°~240°

\begin{align*} 色相H &= 240° - (- \cfrac{R - G}{Imax - Imin} \times 60°) \\\\ &= 240° + \cfrac{R - G}{Imax - Imin} \times 60° \end{align*}

240°~300°

\begin{align*} 色相H &= 240° + \cfrac{R - G}{Imax - Imin} \times 60° \end{align*}

Imax = R の場合

300°~360°

\begin{align*} 色相H &= 360° - (- \cfrac{G - B}{Imax - Imin} \times 60°) \\\\ &= 360° + \cfrac{G - B}{Imax - Imin} \times 60° \end{align*}

0°~60°

\begin{align*} 色相H &= 0° + \cfrac{G - B}{Imax - Imin} \times 60° \\\\ &= \cfrac{G - B}{Imax - Imin} \times 60° \end{align*}

触って学べるサイト

HSV<->RGB 変換ツール

適当なRGB値を入力した上でHSVを変化させてみると、各値の変動の関係性がなんとなく見えてくる。

Hue360

Color SpaceをRGBに設定して、Print User Colorで値を見ながら同一円周上の色を選択していくと、色相環の回転角に応じた値の変化を観察することができる。

https://hue360.herokuapp.com/

参考にしたサイト

色相とRGB値の関係性と各公式

色相とRGB値の関係性を表した図が特にわかりやすい。

https://ofo.jp/osakana/cgtips/hsb.phtml

そもそも色相・明度・彩度って何よ

直観ベースで概念を理解するならこの記事が強すぎる

ガチで数式を考える

学生時代によくお世話になった物理のかぎしっぽさんによるガチ数式

Wiki

Discussion

ログインするとコメントできます