Zenn
📝

[論文メモ] Attention Is All You Need

2023/09/18に公開
機械学習
tech

Attention Is All You Need

読む動機

  • Transformerモデルの理解を深めるため
  • 2023年におけるNLPなどにおいて重要な論文のため

要約

  • 時系列データを変換するモデル(ex. 機械翻訳 など)では再帰(Recurrent)や畳み込み(Convolution)に基づく複雑なNNモデルが主流
  • 既存のSeq2Seqで最も性能のいいモデルは、Attentionを介しEncoderとDecoderを接続している
  • 再帰や畳み込みを完全になくし、Attentionのみで構築したTransformerを提案(=Attention is all you need)
  • 2つの機械学習翻訳タスクで実験を行い、学習時間を大幅に短縮されつつ、性能も優れていることがわかった

背景

  • LSTMやGRUがSequence modelingにおいてSoTA
  • 入力と出力のSequenceの位置に沿って学習を行うため、並列で学習できない(=逐次的な学習である)
    • 時刻tth_{t} は h_{t-1} に依存してしまう

提案手法

Transformer

  • 概観
    • 左側がEncoder, 右側がDecoder
    • self-attentionとpoint-wiseを積み重ねた構造

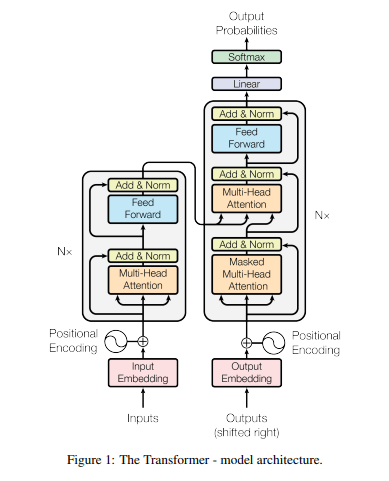
transformer

Encoder and Decoder Stacks

  • Encoder: 入力された列 x = (x_{1}, ... , x_{n}) を隠れ状態の列 z = (z_{1}, ..., z_{n}) に変換

    • N=6の同じレイヤーの積み重ねで構成
    • 各レイヤーには2つのサブレイヤーがある
      • Multi-Head Attention
      • Feed-Forward

  • Decoder: 隠れ状態の列 z = (z_{1}, ..., z_{n}) を出力の列 y = (y_{1}, ... , y_{n}) に変換

    • N=6の同じレイヤーの積み重ねで構成
    • 各レイヤーには3つのサブレイヤーがある
      • Masked Multi-Head Attention
        • 後続のpositionにAttentionしないよう、マスク化
      • Multi-Head Attention
      • Feed-Forward

  • [補足] サブレイヤーについて

    • 各サブレイヤーには以下の処理が加わる
      • 残差接続
      • 正規化
    • → サブレイヤの出力は LayerNorm(x + Sublayer(x))
    • 残差接続を容易にするため、モデル内のすべてのサブレイヤーの出力はEmbeddingと同じく512次元

Attention

  • 概観
    • Attention関数の処理としては、queryとkey-valueペアの出力をマッピングすること
    • 出力はvalueの重み付き和として表される
      • valueに割り振られた重みはqueryとkeyの類似度による
  • Scaled Dot-Product Attention
    • Attention(Q, K, V) = softmax(\frac{QK^{T}}{\sqrt{d_k}})V
      • Q: queryをまとめた行列
      • K: keyをまとめた行列
      • V: valueをまとめた行列
      • d: 次元数
        • 入力列の長さ？

scale-dot-product-attention

  • [補足] Attention funcitonについて

    • よく使われるものとしては以下の2種類
      • additive attention
        • 加法のパターン
        • Softmaxの重み計算部分がFeed-Forward
      • dot-product attention
        • 乗法のパターン
        • √dのスケーリング係数を除いたもの
          • softmax(QK^{T})V
    • dot-product attentionにスケーリングを入れる理由
      • dの値（=入力列の長さ）が大きいと、dot積が大きくなりすぎてしまい、softmax関数によって勾配が極端になってしまうので、打ち消すために√dで割っている

  • Multi-Head Attention

    • query, key, valueをそれぞれh回線形変換し、Attentionを並列
    • 実行結果をconcatしもう一度線形変換すると、最終的なvalueとなる
    • MultiHead(Q, K, V) = Concat(head_{1}, ..., head_{h})W^{o}
      • head_{i} = Attention(QW^{Q}_{i}, KW^{K}_{i}, VW^{V}_{i})
      • W^{Q}_{i}\in R^{d_{model} \times d_{k}}
      • W^{K}_{i}\in R^{d_{model} \times d_{k}}
      • W^{V}_{i}\in R^{d_{model} \times d_{v}}
      • W^{O}\in R^{hd_{v} \times d_{model}}

multi-head-attention

Position-wise Feed-Forward Networks

  • Attentionのサブレイヤーに加えて、Encoder, Decoderそれぞれに完全接続のFeed-Forwardネットワークを入れる
    • 完全接続: 各位置に別々に同じように適用されること
  • 2つの線形変換とReLU活性化関数からなる
    • FFN(x) = max(0, xW_{i} + b_{1})W_{2} + b_{2}
  • 線形変換はレイヤーごとに異なるパラメータを用いる

Embeddings and Softmax

  • Embedding
    • 学習済みEmbeddingを用いて、入力トークンと出力トークンをd_{model}次元のベクトルに変換
  • Softmax
    • Decoder出力では予測される次のトークンを確率に変換

Positional Encoding

  • EncoderスタックとDecoderスタックの一番下にある入力Embeddingに”positional encoding”を追加
    • Transformerには再帰も畳み込みもないので、Sequenceの順序を利用するために、Sequence内のTokenの位置に関する情報を入れる必要がある
      • 相対位置
      • 絶対位置
  • 今回では、異なる周波数のsin・cos関数を使用
    • PE_{(pos, 2i)} = sin(pos /10000^{2i/d_{model}})
    • PE_{(pos, 2i+1)} = cos(pos /10000^{2i/d_{model}})
      • pos: 位置
      • i: 次元
    • この関数を使えば、相対的な位置によるアテンションを容易に学習できる
    • sin関数にした
      • モデルが学習中に遭遇したものより長いSequence長に外挿できる可能性があるから

有効性

  • 機械翻訳

    • データセット

      • WMT 2014 English-German データセット
        • 約450万文のpairからなる
      • WMT 2014 English-French データセット
        • 約3600万文からなる

    • 学習バッチ

      • (約25000のsourceトークン, 約25000のtargetトークン)の形

    • スケジュール

      • Transformer(base model): 10万Epoch
      • Transformer(big): 30万Epoch

    • 結果

      • WMT 2014 English-Germanデータセット
        • Transformer(big): BLUEスコアを2.0以上更新し、SoTA
        • Transformer(base model): 従来のモデルに比べて何分の一かの学習コストでSoTAを達成
      • WMT 2014 English-Frenchデータセット
        • Transformer(big): SoTA

      result-machine-translation

  • 英文の構文解析

    • Transformerが他のタスクに一般化できるかの評価

    • データセット

      • Wall Street Journal(WSJ) データセット

    • 学習方法

      • WSJ only: WSJデータセットの約4万文を学習
      • semi-supervised: 1700万文のBerkleyParserコーパスによる半教師あり学習

    • 結果

      • 構文解析タスクに特化したFine-Tuningがないにも関わらず、とても良い結果を示した
      • Recurrent Neural Network Grammarを除き、従来のモデルよりも良い結果

      result-parsing

備考

  • dot積が大きな値となってしまう理由
    • 平均0, 分散1である独立な確率変数であることを考える
    • q \cdot k = \Sigma^{d_{k}}_{i=1} q_{i}k_{i} の結果は平均0, 分散d_{k}
    • 分散を抑えたいのでスケーリング係数を入れてやる
    • （正規分布などの）標準化の手順と同じ（？）
  • 線形変換

感想

  • 2023年において重要な論文のため、読めて良かった
    • BERTをFine-Tuningしたことがあるが、より理解が深まったと思う
  • 従来のRNNやCNNと比べ、計算量を落としつつ性能も高いので、当時は画期的な論文だったんだろうなーと思った
  • Positional Encodingのsin・cos関数あたりの話がよくわからなかった
  • Attention関数について、そこまで複雑なことをやってはいないことがわかったので、軽くお気持ち実装してみようかなと思った

参考

元論文以上のことが詳しく書いてある

GitHubで編集を提案

Discussion