レヴィ=ストロースの『親族の基本構造』をJavaScriptで理解する
いつものように息抜きのaudibleでレヴィ=ストロースの入門書[1]を読んで聴いていたところ、懐かしいカリエラ族の婚姻制度の話が出てきた。そこで「紙とペンを持って、婚姻関係を書き出してみて」と言われたが、現代人すぎるせいか面倒くさかったのでコードを書いて理解することにした。同じような悩みを抱えている方の理解の助けになればと思う(1人もいない)。
レヴィ=ストロースの名前を初めて聞いたのは学部生の頃で、当時は「構造主義ね。ふーん。」という感じでろくに理解していなかった。ただ最近は良質な音声コンテンツ[2]がたくさん出ているおかげで聴覚優位な私でもとっつきやすくなってきた。(単に個人的な興味が人文社会学に向いてるだけという説もある)
さて本題のカリエラ族についてだが、彼らはオーストラリア北部に住むいわゆる「未開の」先住民族で、図1で示す独特な婚姻制度(=両方交叉いとこ婚)を持つことで知られている。しかもその制度は、どうやら群論という数学の一分野におけるクラインの四元群と同じ「構造」[3]を持っているらしい。
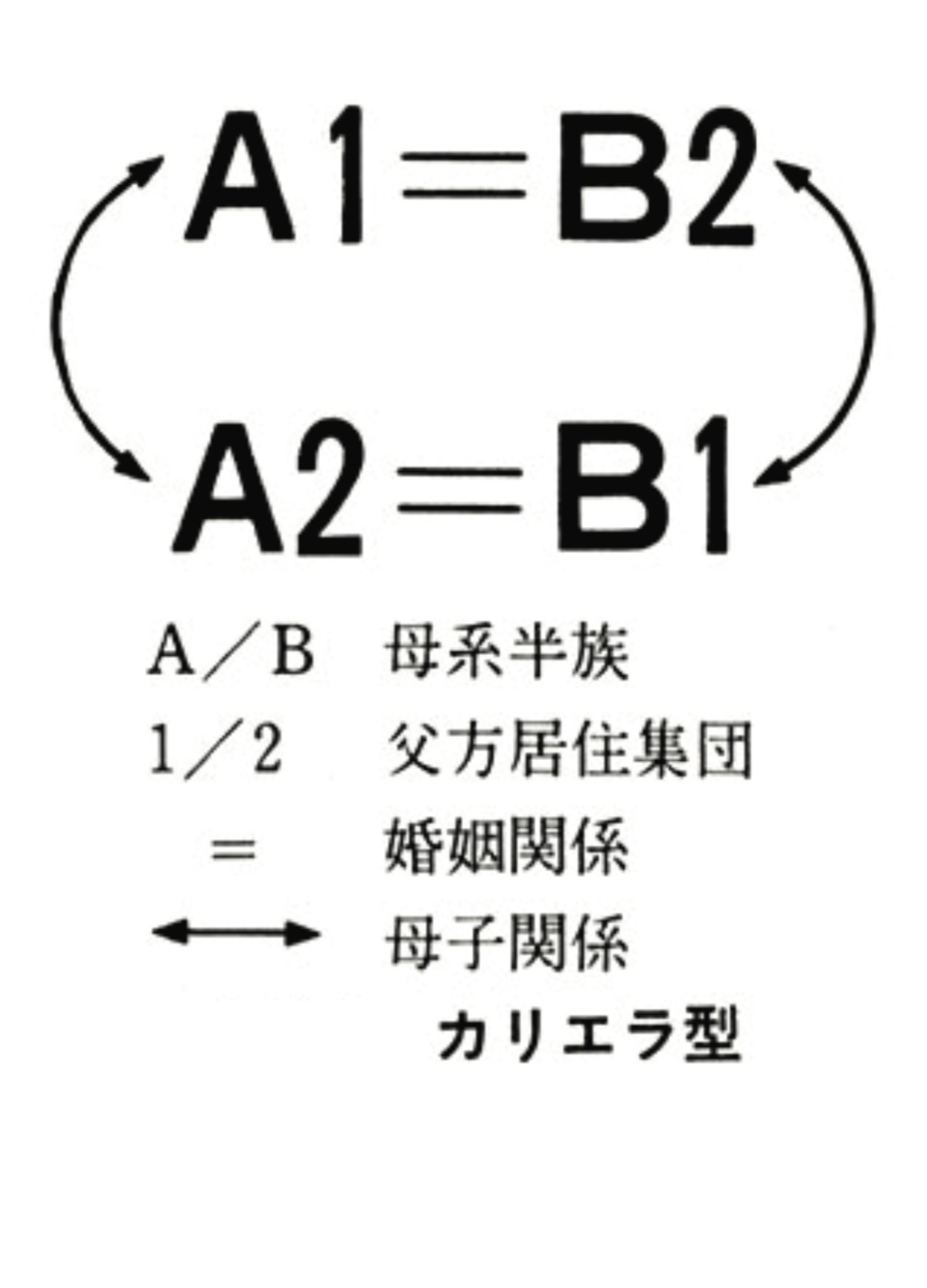
図1 カリエラ族の婚姻制度
検証
できるだけサクッと検証したいので、細かく説明するより先にコードを書き出してみることにする。「面倒くさい」から始まっていることもあり、動的型付け言語の方が良いのと、ブラウザの開発者ツールで動くということでJavaScriptを使うことにした。
とりあえず、配偶者の組み合わせにはルールがあるようなので書く。便宜上、これを婚姻クラスと呼ぶことにする。
const marriageClass = {
1: { male: 'A1', female: 'B2'},
2: { male: 'A2', female: 'B1'},
3: { male: 'B1', female: 'A2'},
4: { male: 'B2', female: 'A1'},
}
図1の=が結婚できる相手らしいので、それを判定する関数を書いてみる。
const getSpouse = (clan, gender) => {
let spouse = null
Object.values(marriageClass).map(rule => {
if (rule.male === clan && gender === 'male') {
spouse = rule.female
}
if (rule.female === clan && gender === 'female') {
spouse = rule.male
}
// 注: 性の二元論的な思想があるわけではなく計算の都合上仕方なくこのような実装になっています
})
return spouse
}
getSpouse('A1', 'male') // B2
これだけではまだわからない。続いて子供の所属を判定する関数を書き出してみる。
const getChildClan = (key) => {
switch (key) {
case 1: // marriageClassのキーに対応
return 'A2'
case 2:
return 'A1'
case 3:
return 'B2'
case 4:
return 'B1'
}
};
getChildClan(1) // A2
ここまで書いて気づいたが、どうやら両親の組み合わせ(1,2,3,4のいずれか)と性別が決まった時点で、子供にとっての配偶者=次世代の両親の組み合わせが決まっているように見える。多分コードにするとこう。
const getChildClan = (key, gender) => {
switch (key) {
case 1:
return gender === 'male' ?
marriageClass[2].male : // 1(A1, B2)の組み合わせで男子が生まれたら、2(A2, B1)のパターン
marriageClass[3].female // 1(A1, B2)の組み合わせで女子が生まれたら、3(B1, A2)のパターン
case 2:
return gender === 'male' ?
marriageClass[1].male : // 以下同様
marriageClass[4].female
case 3:
return gender === 'male' ?
marriageClass[4].male :
marriageClass[1].female
case 4:
return gender === 'male' ?
marriageClass[3].male :
marriageClass[2].female
}
};
getChildClan(1, 'male') // A2
さらにこれをちょっと変形すると、次の配偶者の組み合わせを返す関数が書ける。
const getBoyMarriageClass = (key) => {
switch (key) {
case 1:
return marriageClass[2]
case 2:
return marriageClass[1]
case 3:
return marriageClass[4]
case 4:
return marriageClass[3]
}
};
const getGirlMarriageClass = (key) => {
switch (key) {
case 1:
return marriageClass[3]
case 2:
return marriageClass[4]
case 3:
return marriageClass[1]
case 4:
return marriageClass[2]
}
};
getBoyMarriageClass(1) // これはつまり、1 { male: 'A1', female: 'B2'} の組み合わせで男子が生まれたらその子は2 { male: 'A2', female: 'B1'} の組み合わせでしか結婚できないことを意味する
さて話を戻して、カリエラ族の婚姻制度とクラインの四元群の構造が一致しているということを検証するのがこの記事の目的だった。クラインの四元群については全く専門外だが、ChatGPTによればこういう演算表にすることができるらしい。

あー? この並びどこかで見たな...
// 2, 1, 4, 3
const getBoyMarriageClass = (key) => {
switch (key) {
case 1:
return marriageClass[2]
case 2:
return marriageClass[1]
case 3:
return marriageClass[4]
case 4:
return marriageClass[3]
}
};
// 3, 4, 1, 2
const getGirlMarriageClass = (key) => {
switch (key) {
case 1:
return marriageClass[3]
case 2:
return marriageClass[4]
case 3:
return marriageClass[1]
case 4:
return marriageClass[2]
}
};
男子の婚姻クラスを返す関数と、女子の婚姻クラスを返す関数がそれぞれ2行(列)目3行(列)目の演算と対応している。
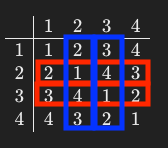
ただ1234,4321についてはよくわからない、、、
と思っていたが、このブログの以下の引用部分を参考にして理解できたようにおもう。
すべて孫の世代は同じ婚姻のタイプになっている。つまりこの変換はfとgのどちらを先にしても同じ変換になる。この変換をhとして、何も変えない恒等変換をiとすると、<i、f、g、h>という4つの変換はクラインの4元群を作る
要するに最初に定義した婚姻クラスをそのままにすることが i = 恒等変換と言えそうだ。
// 1, 2, 3, 4
const marriageClass = {
1: { male: 'A1', female: 'B2'},
2: { male: 'A2', female: 'B1'},
3: { male: 'B1', female: 'A2'},
4: { male: 'B2', female: 'A1'},
}
続いて h についても検証してみる。要するに男女の婚姻クラス変換の関数を順不同で2回使った時、孫世代では4,3,2,1という変換になっていれば良い。もうここまできたら婚姻クラスさえ返してくれれば良いのでコードはこうなる。
// 2, 1, 4, 3
const getBoyMarriageClass = (key) => {
switch (key) {
case 1:
return 2
case 2:
return 1
case 3:
return 4
case 4:
return 3
}
};
// 3, 4, 1, 2
const getGirlMarriageClass = (key) => {
switch (key) {
case 1:
return 3
case 2:
return 4
case 3:
return 1
case 4:
return 2
}
};
const h = (key) => {
const funcs = [getBoyMarriageClass, getGirlMarriageClass]
const shuffled = funcs.sort(() => Math.random() - 0.5)
const childKey = shuffled[0](key) // 男子の変換か女子の変換のいずれか
return shuffled[1](childKey) // 上記で実行されなかった方
}
h(1) // 4
h(2) // 3
h(3) // 2
h(4) // 1
なるほど、確かにそれぞれの関数が群演算のそれと対応していると言えそうです。親族の基本構造、(エンジニア的な意味で)完全理解した。あんまりサクッと終わった感じはしないけど。

おわりに
レヴィ=ストロースは『親族の基本構造』においてカリエラ族より複雑な婚姻形態を持つ民族の分析も行なっており、そちらでは厳密な数学との対応というよりも比喩的に導入されている部分が多い。彼のこの業績の真髄は、カリエラ族のような「未開」とされていた先住民族の婚姻制度と、当時最先端だった現代数学の理論との間に同等の思考様式を見出し、それらが本質的に人間の思考として同じであるという「構造」[4]を取り出したことにあると言える。
-
橋爪大三郎 著. はじめての構造主義, 講談社, 1988.5, (講談社現代新書). 4-06-148898-8, 10.11501/13249651. https://ndlsearch.ndl.go.jp/books/R100000038-I1090344 ↩︎
-
COTEN RADIOの構造主義回 https://podcasts.apple.com/no/podcast/35-1-知の巨人-レヴィ-ストロース-世界を席巻した文化人類学者の足跡-coten-radio-ジンブンガク/id1450522865?i=1000585687244&l=nb ↩︎
-
数学的な意味で使っています ↩︎
-
構造主義的な意味で使っています ↩︎
Discussion