Zenn
🐍

【備忘録】torch.catのdim

に公開
Python
機械学習
PyTorch
tech

torch.catって何しているの？

shape = (2, 3, 4)の3階テンソル[1]に対して、catを施した後の、それぞれのprintの出力結果が想像つきますか？
少なくとも、初見で私は全く想像できませんでした。

そこで備忘録として、torch.catの使い方や、考えのイメージをまとめました。

import torch

shape = (2, 3, 4)
tensor = torch.ones(shape)
print(tensor)
print("--------dim=0---------")
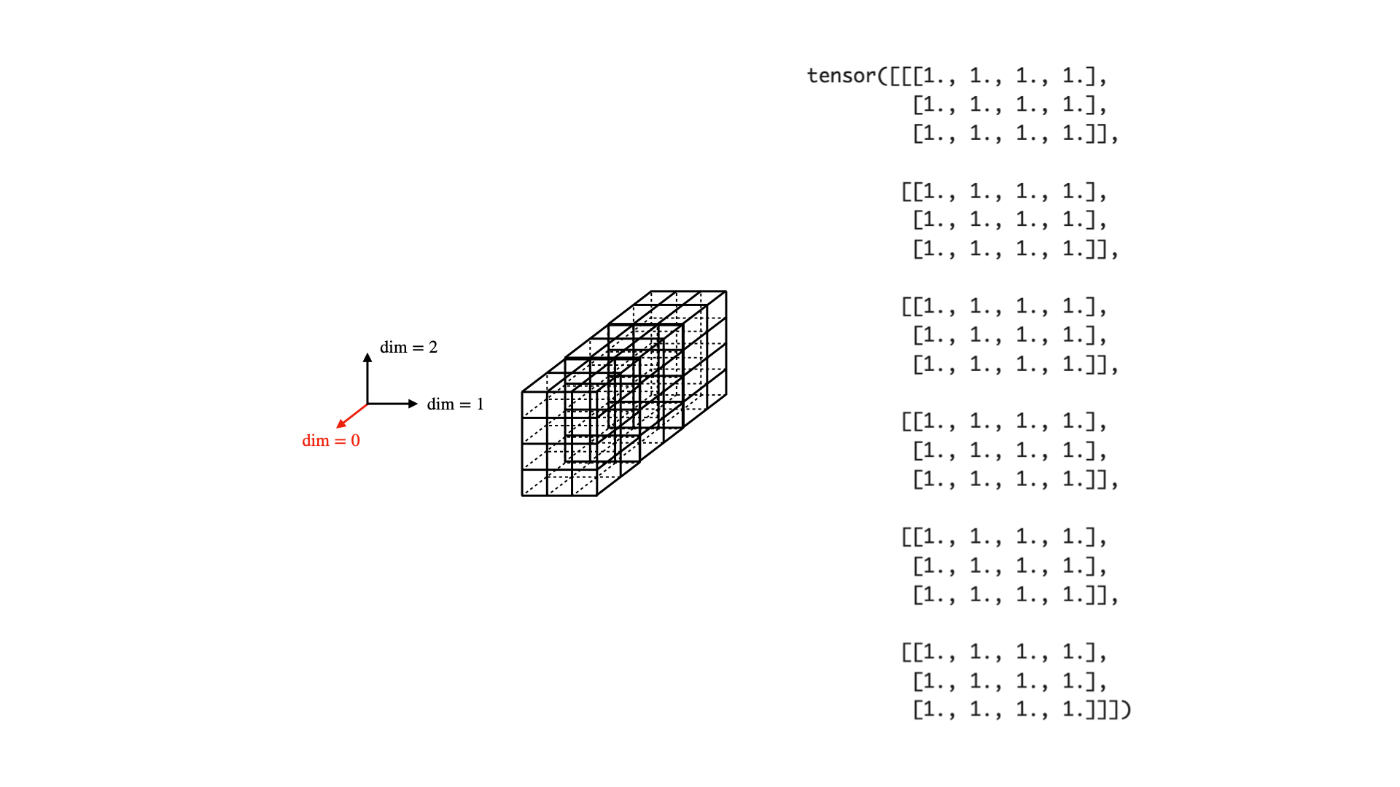
print(torch.cat([tensor, tensor, tensor], dim=0))
print("--------dim=1---------")
print(torch.cat([tensor, tensor, tensor], dim=1))
print("--------dim=2---------")
print(torch.cat([tensor, tensor, tensor], dim=2))

（結果を先に知りたい人はアコーディオンを開いてね）

dim=0
tensor([[[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]],

        [[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]],

        [[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]],

        [[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]],

        [[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]],

        [[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]]])
dim=1
tensor([[[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]],

        [[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]]])
dim=2
tensor([[[1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]],

        [[1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]]])

PyTorch公式による解説

https://docs.pytorch.org/docs/main/generated/torch.cat.html

簡単に訳すと、

（ここから訳）

torch.cat

torch.cat(tensors, dim=0, *, out=None) -> Tensor

指定された次元で、与えられたテンソル列を連結します。すべてのテンソルは同じ形(shape)であるか（連結する次元を除いて）、またはサイズ (0,) のD-1次元の空テンソルでなければなりません。

  • torch.cat()はtroch.split()とtorch.chunk()に対する逆演算子と見なせます。
  • torch.cat()は例を知ることで、ベストな理解が得られます。

（中略）

です。どうやら、複数のテンソルを繋げてくれる関数で、連結する方向に制約があるそうだ。そして、一番ひっかかったのが、連結する次元ってどっちやねんということです。

図解

shape = (2, 3, 4)の3階テンソルは次のようなイメージです。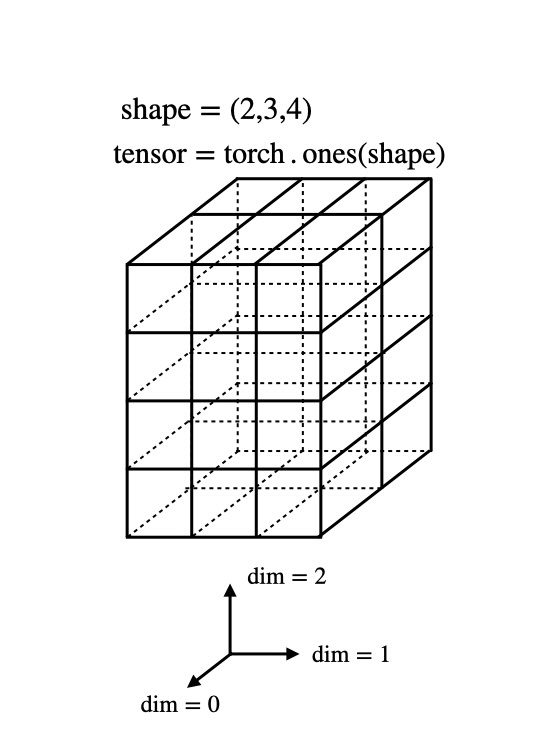
３次元空間の中にある、2 \times 3 \times 4個の小立方体で構成された立体のようなもので、それぞれの小立方体に値が割り振られています。今回はtorch.ones(shape)なので、小立方体の中の値は全て1です。

小立方体のどの値が欲しいかは、３次元空間の位置を示すのと同じように、3つのインデックスを指定します。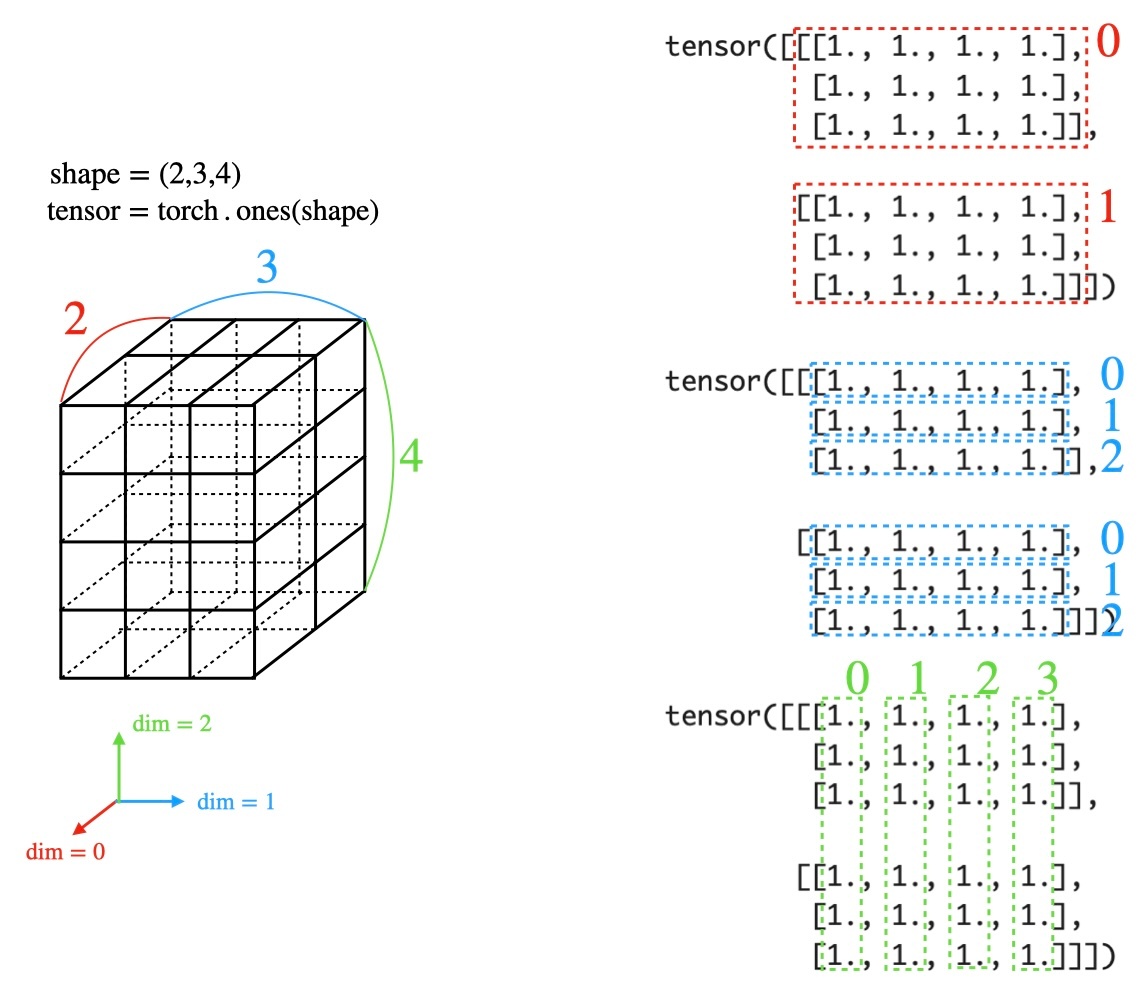

例えば、

tensor = torch.tensor([[[1, 2, 3, 4], 
                        [5, 6, 7, 8], 
                        [9, 10, 11, 12]], 
                       [[13, 14, 15, 16], 
                        [17, 18, 19, 20], 
                        [21, 22, 23, 24]]])

という3階テンソルの場合には、tensor[1][2][0]は21です。

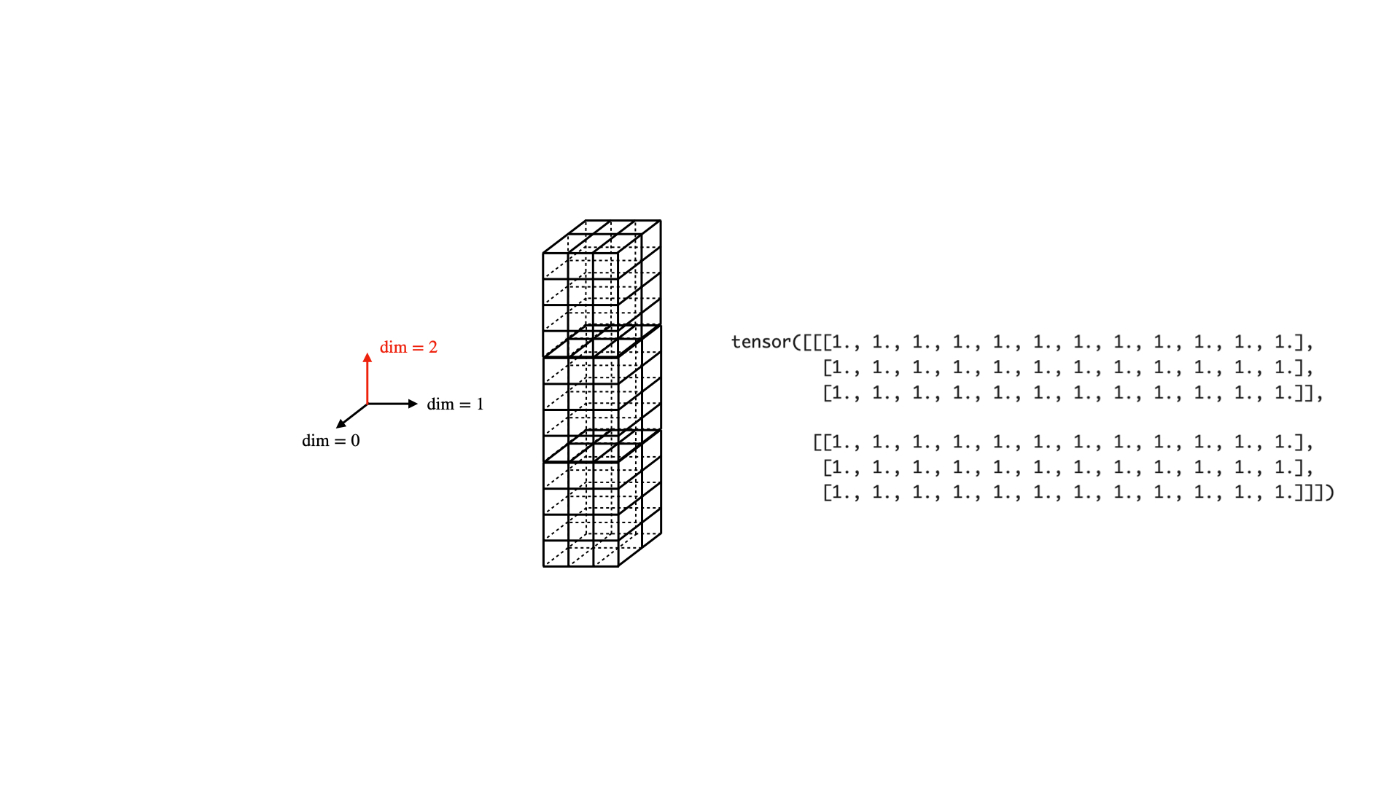
では本題に入ります。torch.catでdimを指定することは、下記のような図で表されます：

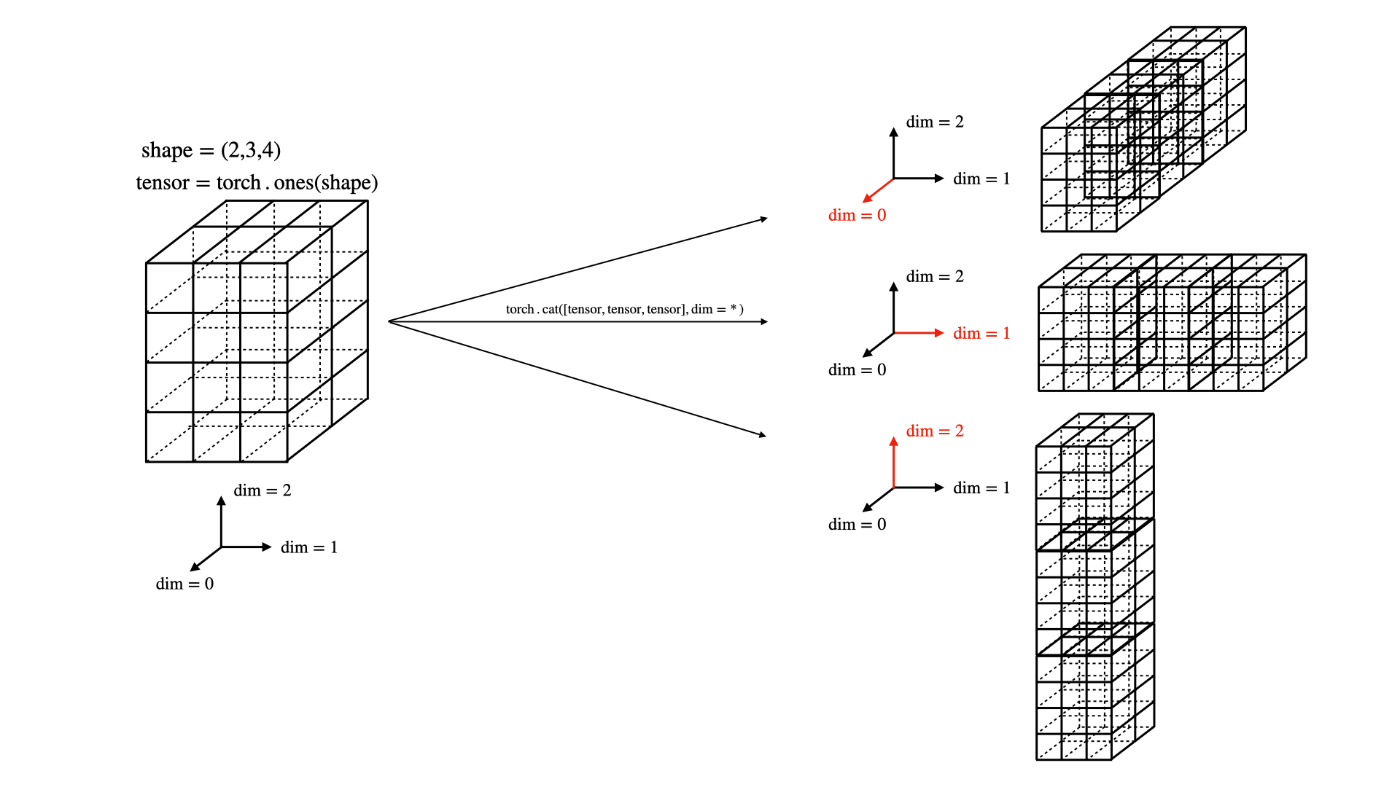
torch.cat([tensor, tensor, tensor], dim=0)

torch.cat([tensor, tensor, tensor], dim=1)

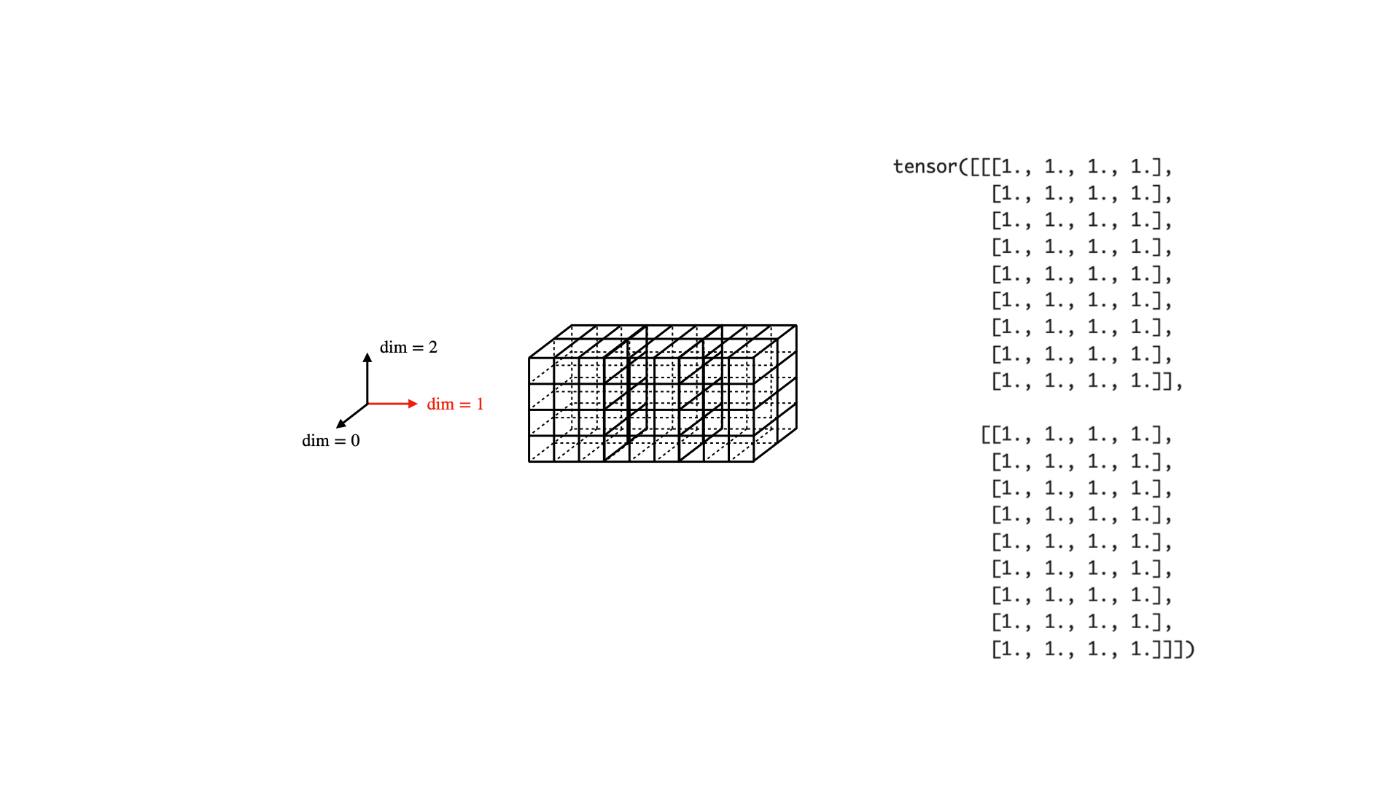
torch.cat([tensor, tensor, tensor], dim=2)

まとめ

図から想像できるように、torch.catは、小立方体で構成された立体(tensor)を繋ぎ合わせます。繋ぎ合わせるときの「接合面」は互いに同じ数の小立体でないといけないため、dimの指定が必要になります。

なので、接合面が一致しておけば、それ以外が一致しなくてもOKです。
例えば、

# shape (2, 2)
tensor1 = torch.tensor([[1, 2], 
                        [3, 4]])

# shape (3, 2)
tensor2 = torch.tensor([[5, 6], 
                        [8, 9], 
                        [10, 11]])

# shape(5, 2)
tensor3 = torch.cat([tensor1, tensor2], dim=0)
print(tensor3)
>>>tensor([[ 1,  2],
        [ 3,  4],
        [ 5,  6],
        [ 8,  9],
        [10, 11]])

ですね。

一般に、n+1階テンソルにおいて、shape = (a_0, a_1, ..., a_i, ..., a_n)のテンソルとshape = (b_0, b_1, ..., b_i, ..., b_n)があると、a_i = b_i(ただし、0 \leq l \leq nを除く)ならば、dim=l方向にtorch.cat可能ということです。

脚注

  1. 数学、物理の分野では、テンソルは単に複数の成分を持った量を意味しません。特に物理学では、テンソルは座標に依存しない量で、テンソルの成分は座標変換に対する変換生を持ちます。話が噛み合わない時は、相手の専門分野を聞いてみましょう。 ↩︎

Discussion