🌊
シンプルな物理知ニューラルネットワーク (PINN: Physics-Informed Neural Network)

2025/04/18に公開
 導入2019年ごろに報告されたPhysics-informed neural network (PINN) [1]は、物理における法則・対称性を誤差関数として落とし込み、その物理の系の性質をよく表した解をNeural Networkで導くことができる手法の1つです。
ネットで探せば[2]といった日本語での記事は見つかりますが、Burgers方程式（流体関連の方程式）という全然introductoryではない方程式を例として解析しています。
そこで、本記事ではBurgers方程式ではなく、理工学系の学生や、理工学について学んだことのある社会人の方々の多くがきっと既知であろう方程式、波動方程式を使って議論したいとおもいます。
波動方程式の利点としては多くの人が既知である他、初期条件・境界条件を適切に設定することで、高校生でも分かる形の厳密解に帰着することができるようになります。この厳密解を使えば、PINNで予言された関数と厳密解の比較も容易になります。比較することで、最適なハイパーパラメタについても議論します。
この記事は次のように構成されています。まずは§解析パートで波動方程式の厳密解を簡単に導き、PINNについても紹介します。§設定パートでは、使用したパラメタを紹介します。次の§結果パートでは最も良いハイパーパラメタの組み合わせ、重みと学習率の関係について議論します。最後考察と展望があります。

 解析
 波動方程式理・工学系の多くの大学生のおそらくほとんどが目にしたことのある、基本的な偏微分方程式「波動方程式」を取り扱いましょう！✨
なるべく問題をシンプルにするために1次元の波（例：弦とか）を考えます。x軸上で時刻tでの波の振幅（高さ）をu(t, x)とします。
このとき、1次元の波は次の偏微分方程式を満たします：

    \left(
    - \frac{1}{c^2} \frac{\partial^2}{\partial t^2}
    + \frac{\partial^2}{\partial x^2}
    \right) 
    u(t, x) = 0
ここでcは波の速さで、以降は簡単のために1としています。

 定義域x = [-1, 1]
t = [0, 1]


 境界条件と初期条件境界条件：u(t, -1) = u(t, 1) = 0　（固定端）

初期条件：
u(0, x) = \sin(\pi x)
\left.\frac{\partial u}{\partial t}\right|_{t=0} = 0

 解析解波動方程式の一般解はd'Alembertの解として

    u(t, x) = f(x - ct) + g(x + ct)
と任意関数f, gで表すことができます。しかし、数値計算をしたいときに、上記のような一般的な解を持ってこられても困るわけです。そこで今回設定した初期条件・境界条件における特殊解を（すごーく雑に）求めましょう。
🔸STEP1 解を予想する

解を予想しましょう。時間と空間の2回微分が等しいという条件から次が予想できます：

    u(t, x) = A\sin(k x) \sin(\omega t + \alpha) 
ここでAは振幅、kは波数、\alphaは位相です。両方の\sinに位相パラメタが現れそうですが、適当な座標変換をすれば、任意性を1つの位相に押し付けられます。
🔸STEP2　条件を適用

境界条件・初期条件を予想した解に対して適用し、未知のパラメタを決定します。すると解は

    u_{\rm exact}(t, x) = \sin(\pi x) \cos(\pi t)
となります。

 PINNPINNは物理学の系の情報を用いて順問題と逆問題に対応できる手法です。詳細な議論に関しては[1]や[3]に譲るとして、ここでいう順問題・逆問題とは下記の通りです：
順問題　微分方程式を解くこと
逆問題　データに整合する方程式を求めること
今回は単純に波動方程式を解きたいので順問題に対応します。
さて、PINNの肝である式である次を紹介します。

    f(t, x) :=  \left(
    - \frac{1}{c^2} \frac{\partial^2}{\partial t^2}
    + \frac{\partial^2}{\partial x^2}
    \right) 
    u(t, x)
これは一見、波動方程式の左辺（冒頭で紹介した式）をそのままtとxの関数にしたものです。実はこれが非常に重要なアイディア（だと自分は思っていて）で、このfが0になるよう学習を進めていけば、波動方程式の解がもとまるよね、という論理です。
もちろん、通常解く場合、上記の解析解の節でも述べたように初期条件や境界条件も必要です。これも同様に式u(t=0, x) = f(x) = 0やu(t, x=x_b) = g(t) = 0のように書くことができて、これを満たすように学習していけば解が求まります。
言い換えれば、波動方程式、境界条件、初期条件に対する誤差関数{\rm EMS}_0, {\rm EMS}_b, {\rm EMS}_fを定義し、

    {\rm MSE}_{\rm tot}
    =
    w_i{\rm MSE}_i
    + w_b {\rm MSE}_b
    + w_f {\rm MSE}_f
が最小になるよに確率的勾配法やAdamといった手法で誤差関数の値を更新すればよいのです。ここでは二乗平均誤差を仮定し、w_i, w_b, w_fはweightです。この後の議論ではw_i, w_bは1としています。

 設定厳密解u_{\rm exact}とPINNによって予言された解u_{\rm pred}の比較するために次のような量を導入します：

    {\cal E} 
    := \int_\Omega {\rm d} t {\rm d} x \,
    | u_{\rm pred}(t, x) - u_{\rm exact}|
u_{\rm pred}とu_{\rm exact}の値が近ければ近いほど、この誤差{\cal E}の値は0に近づきますので、この量が小さいほど「良い」モデルとします。積分するときに負の値が含まれると打ち消されてしまうので、絶対値がつきます。
（この量は機械学習の分野ではL_1誤差であったり、数学でいうL_pノルムのp=1のとき（マンハッタン距離）だったりします）
\Omegaは非積分関数の定義域でt = [0, 1], x = [-1, 1]を走ります。
また、今回使う全てのパラメタは下記で設定しております。
初期条件のサンプルポイント数　N_i = 100
境界条件のサンプルポイント数　N_b = 100
領域内のサンプルポイント数　　N_f = 5000
隠れ層とそのサイズ　　　　　　32, 64, 128, 64, 32

エポック数　　　　　　　　　　{\rm epoch} = 100, 500, 1000, 2000, 3000, 4000, 5000

学習率　　　　　　　　　　　　\eta = 0.0001, 0.0005, 0.001, 0.005, 0.01

重み　　　　　　　　　　　　　w_f = 0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1
特に、エポック数、学習率、重みを今回は変化させ、それ以外については固定します。
初期条件のサンプルポイント数、境界条件のサンプルポイント数、領域ないのサンプルポイント数のイメージは下記の図を確認してみてください。

 結果
 最も良いパラメタ今回設定したエポック数、学習率、重みの量を動かしたとき、もっとも{\cal E}が小さくなるパラメタの組み合わせは
エポック数　　　　　　　　　　{\rm epoch} = 3000
学習率　　　　　　　　　　　　\eta = 0.0005
重み　　　　　　　　　　　　　w_f = 0.01
でした。
このときのロスの履歴は

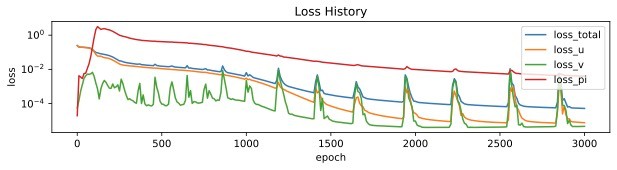
となっています。{\rm EMS}_{\rm tot}（青線）は最終的に{\cal O}(10^{-4})程度まで下がっていますね。
予言された関数のcontour plotは次のように与えられます。

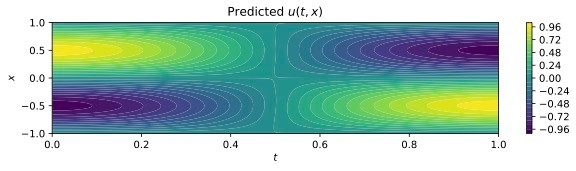
また、時間ごとにスライスしたときの２次元プロットは



で表されます。それぞれ5枚のプロットは時刻t = 0, 0.25, 0.5, 0.75, 1におけるu-xグラフになります。青線がPINNによって得られた関数u_{\rm pred}、黒の点線が厳密な関数u_{\rm exact}、そしてオレンジ線が残差f(t, x)です。このf(t, x)が0になるように学習しており、さらに誤差関数として1以下の重みがかけられたものが誤差関数の総計として加算されます。そのため、誤差関数としては、重みのせいでf由来の誤差の寄与が小さくなっている、もしくは他の誤差関数とのオーダーを合わせている、とここで言及しておきます。

 重みと学習率横軸を重み、縦軸を学習率としたときのヒートマップです。色はエポック数に対する{\rm EMS}_{\rm tot}を表しています。
この図を見ると
学習率　　0.01
重み　　　0.005
あたりが良い結果を与える傾向にありますね。前節で述べた最も良いパラメタとは異なることに注意されたいです。

 考察と展望今回の記事ではPINN (Physics-informed neural network)によって波動方程式を解きました。動かしたパラメタはエポック数、学習率、誤差関数（MSE）の関数の残差に対する重みです。最も良い結果を与えたのは
エポック数　　　　　　　　　　{\rm epoch} = 3000
学習率　　　　　　　　　　　　\eta = 0.0005
重み　　　　　　　　　　　　　w_f = 0.01
でした。
しかし、傾向としては学習率は0.01の方が平均的には誤差関数を小さくします。

おそらく確率的勾配法が使われている部分で、たまたま良い解に乗ったのかもれません。また、残差fに対する重みが1の方が結果が悪いです。これは他の種類のMSEとのオーダーが違いすぎるからですかね……。ロスの履歴を見ると残差由来の方が、他の全ての誤差に対して２桁程度大きいです。ただ、普通に考えてこの残差が0になるということが、目的の偏微分方程式を解くことに対応するので、個人的にこの結果はまだ受け止めることができない精神状況です笑
機械学習の専門家ではないので、詳細に何が起きているかは今後調査するポイントですね。

これからもっと勉強していい記事書こうと思いますので、よろしくお願いします！！🙇

 参考文献[1] M. Raissi, P. Perdikaris, G. E. Karniadakis, 'Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations', Journal of Comutational Physics Vol 378, 1, 686-707 (2019) [https://www.sciencedirect.com/science/article/abs/pii/S0021999118307125]
[2] https://www.atmosphere-eng.com/posts/240304_pinn
[3] 橋本 幸士（編）、富谷昭夫、金子隆威、瀧雅人、広野雄士、唐木田亮、三内顕義「学習物理学　Introduction to Machine Learning Physics」 (2024) 朝倉書店, https://www.asakura.co.jp/detail.php?book_code=13152&srsltid=AfmBOoqzaN80KLzm0Kd5YN6Fw4-T1S1Ao7CkLP-1MxlataacCdyRuoN9

 外部リンクhttps://github.com/inuverse44/simple_pinn