曲面上の平行移動と共変微分

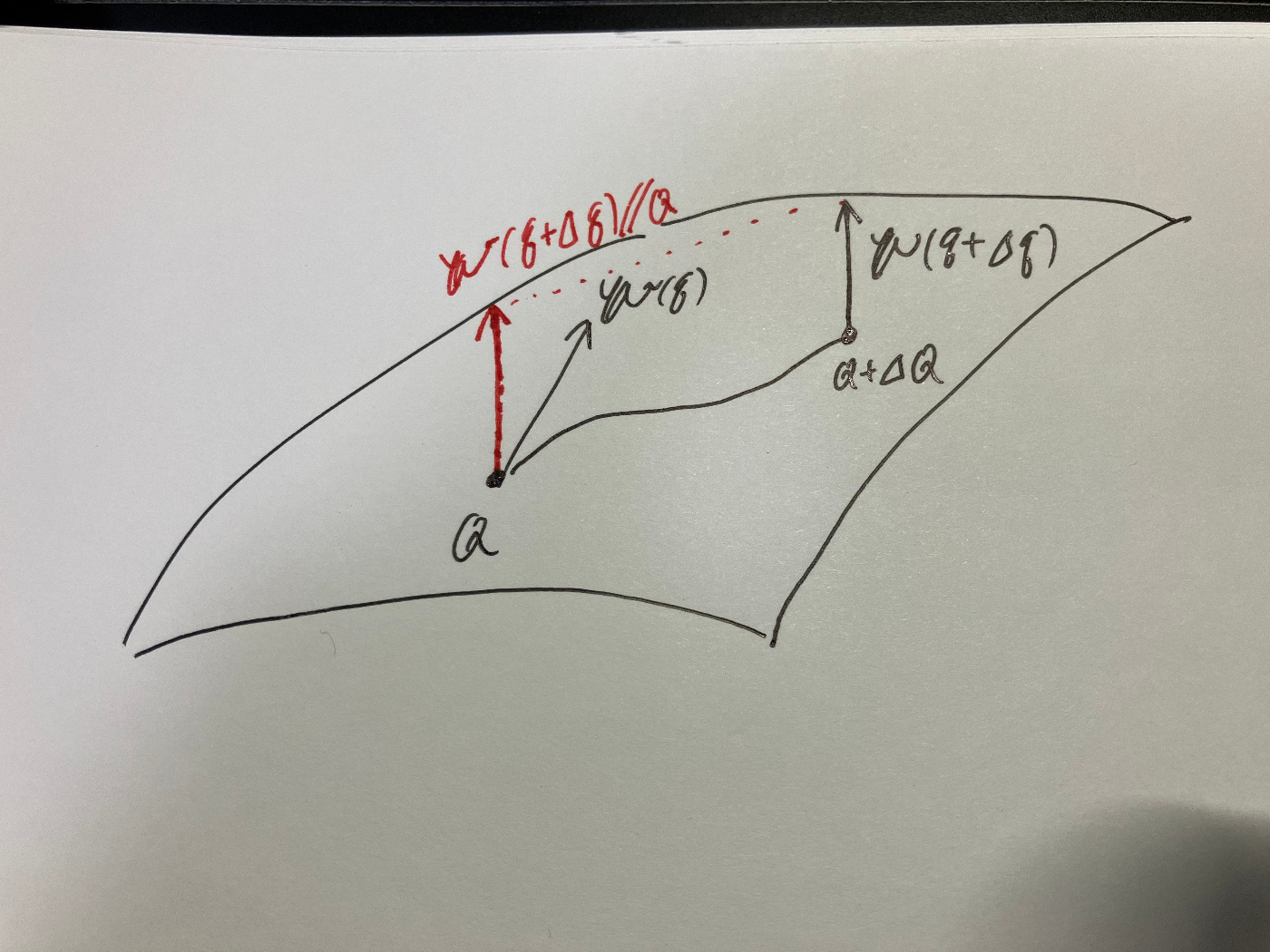
反変ベクトル成分の平行移動

\boldsymbol{r}(q) で表される曲面上の接ベクトル \boldsymbol{w} を以下のように定義する：

\boldsymbol{w} = w^i \frac{\partial \boldsymbol{r}}{\partial q^i}.

接ベクトル \boldsymbol{w} は曲面上の点 Q と点 Q+\Delta Q を通る曲線上を移動しているとして、点 Q+\Delta Q における接ベクトル \boldsymbol{w}(q+\Delta q) を点 Q に平行移動した際の成分を以下のように表すことができる：

\begin{aligned} w^i(q + \Delta q)_{//Q} = w^i(q) + \frac{\partial w^i(q)}{\partial q^k} \Delta q^k + \Gamma^i_{jk}(q)w^j(q) \Delta q^k + \Omicron((\Delta q)^2). \end{aligned}

クリストッフェル記号 \Gamma^i_{jk} は、以下を満たすように定義される：

\frac{\partial^2\boldsymbol{r}}{\partial q^j \partial q^k} = \Gamma^{i}_{jk}\frac{\partial \boldsymbol{r}}{\partial q^i} + h_{ij} \boldsymbol{e}_N

\boldsymbol{e}_N は、曲面の放線方向を向く単位ベクトルである。

点 Q に平行移動したベクトル成分 w^i(q + \Delta q)_{//Q} と点 Q におけるベクトル成分 w^i(q) をもちいて、以下のような時間微分が求められる：

\begin{aligned} \lim_{\Delta t \to 0} \frac{w^i(q + \Delta q)_{//Q} - w^i(q)}{\Delta t} &= \frac{dq^k}{dt} \left( \frac{\partial w^i}{\partial q^k} + \Gamma^i_{jk}w^j \right)\\ &= \frac{dw^i}{dt} + \Gamma^i_{jk}w^j \frac{dq^k}{dt} \end{aligned}

ベクトル \boldsymbol{w} の時刻 t による微分は以下のように表されるが、上記の時間微分成分はこの二行目の第一項の括弧内と一致する：

\begin{aligned} \frac{d\boldsymbol{w}}{dt} &= \frac{dw^i}{dt} \frac{\partial \boldsymbol{r}}{\partial q^i} + w^i \frac{dq^j}{dt}\frac{\partial^2 \boldsymbol{r}}{\partial q^i \partial q^j}\\ &= \frac{\partial \boldsymbol{r}}{\partial q^i} \left( \frac{dw^i}{dt} + \Gamma^i_{jk}w^j \frac{dq^k}{dt} \right) + h_{ij} w^i \frac{dq^j}{dt} \boldsymbol{e}_N. \end{aligned}

なお、上記では平行移動を w^i(q+\Delta q) を点 Q+\Delta Q から Q に持ってくる形で定義したが、それとは逆方向に w^i(q) を点 Q から Q+\Delta Q へ持って行くように定義する場合もある：

w^i(q)_{//Q+\Delta Q} = w^i(q) - \Gamma^i_{jk}(q) w^j(q)\Delta q^k + \Omicron((\Delta q)^2)

この場合、

\lim_{\Delta t \to 0} \frac{w^i(q+\Delta q) - w^i(q)_{//Q+\Delta Q}}{\Delta t} = \frac{dw^i}{dt} + \Gamma^i_{jk}w^j \frac{dq^k}{dt}.

共変微分

反変ベクトル成分 w^i の共変微分は、以下のように定義できる：

\nabla_k w^i = \frac{\partial w^i}{\partial q^k} + \Gamma^i_{jk} w^j.

これを用いると、以下のように表すことができる：

\begin{aligned} \lim_{\Delta t \to 0} \frac{w^i(q + \Delta q)_{//Q} - w^i(q)}{\Delta t} &= \frac{dq^k}{dt} \left( \frac{\partial w^i}{\partial q^k} + \Gamma^i_{jk}w^j \right)\\ &= \frac{dq^k}{dt} \nabla_k w^i, \end{aligned}

\begin{aligned} \frac{d\boldsymbol{w}}{dt} &= \nabla_k w^i \frac{dq^k}{dt} \frac{\partial \boldsymbol{r}}{\partial q^i} + h_{ij} w^i \frac{dq^j}{dt} \boldsymbol{e}_N. \end{aligned}

共変ベクトル成分の場合の平行移動と共変微分

共変ベクトル成分 A_l については以下のように平行移動と共変微分を定義できる：

A_l(q+\Delta q)_{//Q} = A_l(q) + \frac{\partial A_l(q)}{\partial q^m} \Delta q^m - \Gamma^k_{lm} A_m(q)\Delta q^m + \Omicron((\Delta q)^2)

\nabla_m A_l = \frac{\partial A_l}{\partial q^m} - \Gamma^k_{lm} A_k

これらを用いると、

\begin{aligned} \lim_{\Delta t \to 0} \frac{A_l(q+\Delta q)_{//Q} - A_l(q)}{\Delta t} &= \frac{dq^m}{dt}\left( \frac{\partial A_l}{\partial q^m} - \Gamma^k_{lm} A_k \right)\\ &= \frac{dq^m}{dt}\nabla_m A_l. \end{aligned}

なお、こちらも逆方向に定義すると、

A_l(q)_{//Q+\Delta Q} = A_l(q) + \Gamma^k_{lm}(q) A_k(q)\Delta q^m + \Omicron((\Delta q)^2)

\lim_{\Delta t \to 0} \frac{A_l(q+\Delta q) - A_l(q)_{//Q+\Delta Q}}{\Delta t} = \frac{dq^m}{dt}\nabla_m A_l.

補足： 反変・共変間の変換

計量テンソル

g_{ij} = \frac{\partial \boldsymbol{r}}{\partial q^i} \cdot \frac{\partial \boldsymbol{r}}{\partial q^j}

の逆行列を g^{kl} と表す（g^{il} g_{lj} = \delta_{ij}）。

このとき、

g^{il} \nabla_m A_l = \nabla_m A^i

が成り立つ。

証明

まず、上記の式の左辺は以下のように変形することができる：

\begin{aligned} g^{il} \nabla_m A_l &= g^{il}\frac{\partial A_l}{\partial q^m} - g^{il}\Gamma^{k}_{lm}A_k\\ &=g^{il}\frac{\partial A_l}{\partial q^m} - g^{il}g^{jk}\Gamma_{jlm}A_k\\ &=g^{il}\frac{\partial A_l}{\partial q^m} - g^{il}\Gamma_{jlm}A^j. \end{aligned}

ここで、

g^{il} A_l = A^i

より、

\begin{aligned} \frac{\partial A^i}{\partial q^m} &= \frac{\partial (g^{il} A_l)}{\partial q^m}\\ &= \frac{\partial g^{il}}{\partial q^m}A_l + g^{il} \frac{\partial A_l}{\partial q^m}\\ &= \frac{\partial g^{il}}{\partial q^m} g_{lj} A^j + g^{il} \frac{\partial A_l}{\partial q^m}\\ \end{aligned}

が成り立ち、さらに g^{il} g_{lj} = \delta_{ij} より、

\begin{aligned} \frac{\partial g^{il}}{\partial q^m} g_{lj} &= - g^{il} \frac{\partial g_{lj}}{\partial q^m}\\ &= -g^{il}(\Gamma_{ljm} + \Gamma_{jlm}) \end{aligned}

が成り立つので、

\begin{aligned} g^{il}\frac{\partial A_l}{\partial q^m} &= \frac{\partial A^i}{\partial q^m} - \frac{\partial g^{il}}{\partial q^m} g_{jl} A^j\\ &= \frac{\partial A^i}{\partial q^m} + g^{il}(\Gamma_{ljm} + \Gamma_{jlm}) A^j\\ \end{aligned}

が成立する。

以上を先ほどの式に代入すると、

\begin{aligned} g^{il} \nabla_m A_l &=g^{il}\frac{\partial A_l}{\partial q^m} - g^{il}\Gamma_{jlm}A^j\\ &= \frac{\partial A^i}{\partial q^m} + g^{il}(\Gamma_{ljm} + \Gamma_{jlm}) A^j- g^{il}\Gamma_{jlm}A^j\\ &= \frac{\partial A^i}{\partial q^m} + g^{il}\Gamma_{ljm} A^j\\ &= \frac{\partial A^i}{\partial q^m} + \Gamma^i_{jm} A^j\\ &= \nabla_m A^i. \end{aligned}

参考文献

• 山本義隆、中村孔一「解析力学I（朝倉物理学大系）」（朝倉書店、1998）
  https://amzn.asia/d/ikEkb89

• 藤井保憲「時空と重力（物理学の回廊）」（産業図書、1979）
  https://amzn.asia/d/9SXmTCb

リーマン曲率テンソル

曲面上の平行移動は、動かす経路に依存する。

経路によってどれだけ平行移動後のベクトルに差が現れるかを見るために、以下のように共変ベクトル成分 A_l(q) を点 P から点 R まで2通りの異なる経路で平行移動した際の差を計算する。

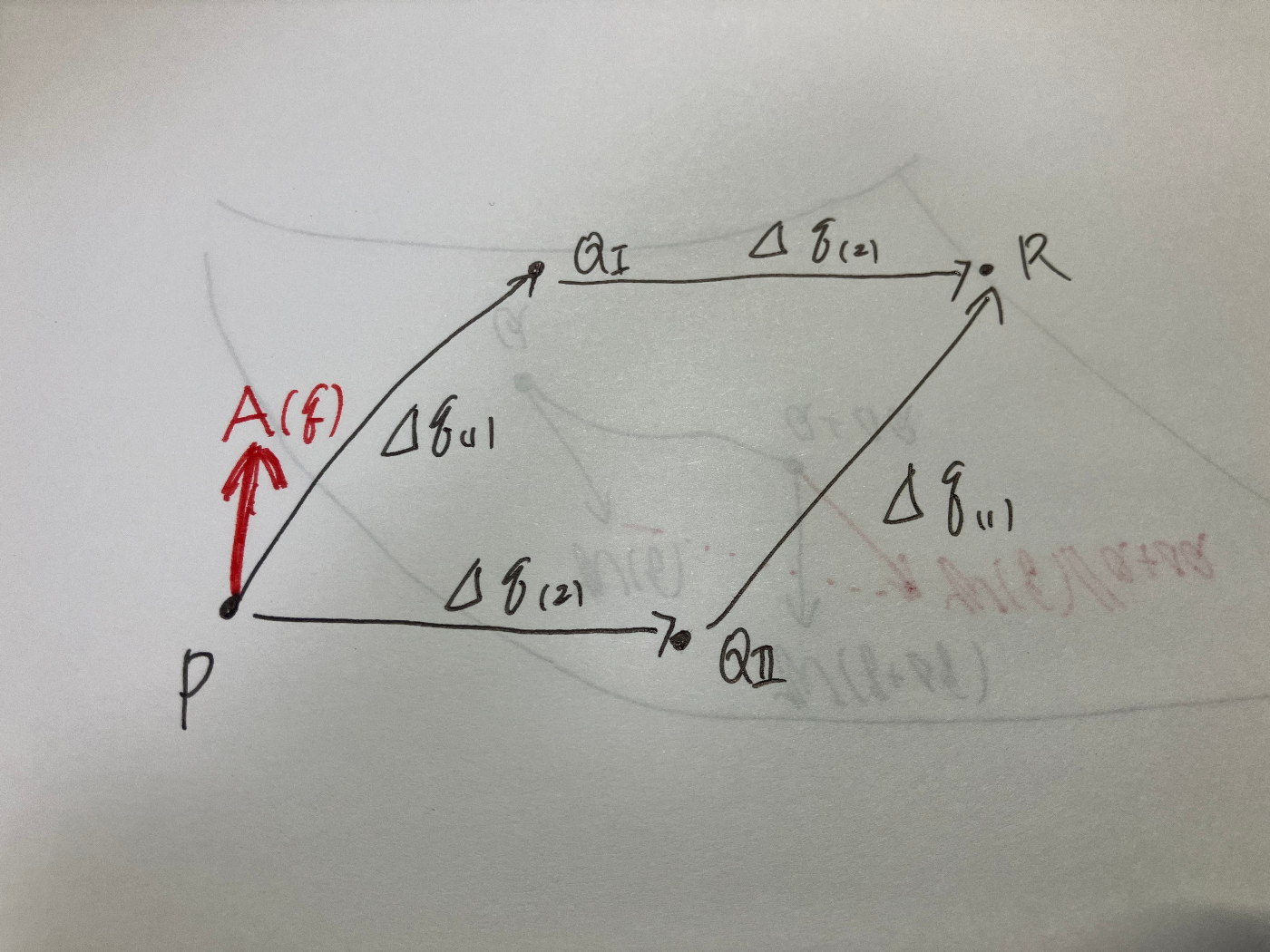
その結果は以下のようになる：

A_l(q)_{//Q_I //R} - A_l(q)_{//Q_{II}//R} = R^{k}_{\,lmn} A_k(q) \Delta q^m_{(1)} \Delta q^n_{(2)} + \Omicron((\Delta q)^3)

ここで、R^{k}_{\,lmn} はリーマン曲率テンソルと呼ばれ、以下のように定義される：

R^{k}_{\,lmn} = \frac{\partial \Gamma^k_{\,ln}}{\partial q^m} - \frac{\partial \Gamma^k_{\,lm}}{\partial q^n} + \Gamma^{k}_{\,jm}\Gamma^{j}_{\,ln} - \Gamma^{k}_{\,jn}\Gamma^{j}_{\,lm}.

なお、上記では共変ベクトル成分 A_l で考えたが、反変ベクトル成分 w^i でも符号が反転するものの同様の結果が得られる：

w^i(q)_{//Q_I //R} - w^i(q)_{//Q_{II}//R} = -R^{i}_{\,jkl} w^j(q) \Delta q^k_{(1)} \Delta q^l_{(2)} + \Omicron((\Delta q)^3)

逆向きの平行移動による計算

上記では参考文献に挙げた教科書（[藤井1979]）に従い点 P におけるベクトル成分 A_l(q) を点 R に動かすことを考えた。

ここでは練習問題を兼ねて逆に点 R におけるベクトル成分 A_l(q + \Delta q_{(1)} + \Delta q_{(2)}) を点 P へと「逆向き」に移す場合について計算してみた結果、以下のようになった：

A_l(q + \Delta q_{(1)} + \Delta q_{(2)})_{//Q_I//P} -A_l(q + \Delta q_{(1)} + \Delta q_{(2)})_{//Q_{II}//P} \\= - R^{k}_{\,lmn} A_k(q) \Delta q^m_{(1)} \Delta q^n_{(2)} + \Omicron((\Delta q)^3).

導出

通常、Q+\Delta Q \to Q の平行移動は以下のように表す：

A_l(q+\Delta q)_{//Q} = A_l(q) + \frac{\partial A_l(q)}{\partial q^m} \Delta q^m - \Gamma^{k}_{\,lm}(q) A_k(q) \Delta q^m

これを、以下から \Delta q のオーダーだけ残したものとして捉える：

A_l(q+\Delta q)_{//Q} = A_l(q+\Delta q) - \Gamma^{k}_{\,lm}(q) A_k(q+\Delta q) \Delta q^m.

これを用いて、まず R \to Q_I の平行移動を考える。

A_l(q + \Delta q_{(1)} + \Delta q_{(2)})_{//Q_I} = A_l(q + \Delta q_{(1)} + \Delta q_{(2)}) - \Gamma^{k}_{\,ln}(q + \Delta q_{(1)})A_k(q + \Delta q_{(1)} + \Delta q_{(2)})\Delta q^n_{(2)}.

ここで、

\begin{aligned} A_l(q + \Delta q_{(1)} + \Delta q_{(2)}) &= A_l(q + \Delta q_{(1)}) + \frac{\partial A_l(q + \Delta q_{(1)})}{\partial q^n}\Delta q^n_{(2)} + \frac{1}{2} \frac{\partial^2 A_l(q + \Delta q_{(1)})}{\partial q^n \partial q^m}\Delta q^n_{(2)}\Delta q^m_{(2)} + \Omicron((\Delta q)^3)\\ \end{aligned}

であるので、

\begin{aligned} A_l(q + \Delta q_{(1)} + \Delta q_{(2)})_{//Q_I} &= A_l(q + \Delta q_{(1)}) + \frac{\partial A_l(q + \Delta q_{(1)})}{\partial q^n}\Delta q^n_{(2)} + \frac{1}{2} \frac{\partial^2 A_l(q + \Delta q_{(1)})}{\partial q^n \partial q^m}\Delta q^n_{(2)}\Delta q^m_{(2)}\\ &\qquad - \Gamma^{k}_{\,ln}(q + \Delta q_{(1)})A_k(q + \Delta q_{(1)})\Delta q^n_{(2)}\\ &\qquad - \Gamma^{k}_{\,ln}(q + \Delta q_{(1)})\frac{\partial A_k(q + \Delta q_{(1)})}{\partial q^m} \Delta q^n_{(2)}\Delta q^m_{(2)} + \Omicron((\Delta q)^3) \end{aligned}

のように表すことができる。

さらにこれを Q_I \to P に平行移動すると、以下のようになる：

\begin{aligned} A_l(q + \Delta q_{(1)} + \Delta q_{(2)})_{//Q_I//P} &= A_l(q + \Delta q_{(1)} + \Delta q_{(2)})_{//Q_I} - \Gamma^k_{\,lm}(q)A_k(q + \Delta q_{(1)} + \Delta q_{(2)})_{//Q_I} \Delta q_{(1)}^m\\ &=A_l(q + \Delta q_{(1)}) + \frac{\partial A_l(q + \Delta q_{(1)})}{\partial q^n}\Delta q^n_{(2)} + \frac{1}{2} \frac{\partial^2 A_l(q + \Delta q_{(1)})}{\partial q^n \partial q^m}\Delta q^n_{(2)}\Delta q^m_{(2)}\\ &\qquad - \Gamma^{k}_{\,ln}(q + \Delta q_{(1)})A_k(q + \Delta q_{(1)})\Delta q^n_{(2)}\\ &\qquad - \Gamma^{k}_{\,ln}(q + \Delta q_{(1)})\frac{\partial A_k(q + \Delta q_{(1)})}{\partial q^m} \Delta q^n_{(2)}\Delta q^m_{(2)}\\ &\qquad - \Gamma^k_{\,lm}(q) \left\{ A_k(q+\Delta q_{(1)}) + \frac{\partial A_k(q + \Delta q_{(1)})}{\partial q^n}\Delta q^n_{(2)}\right.\\ &\qquad \qquad \qquad \qquad \left. - \Gamma^{j}_{\,kn}(q + \Delta q_{(1)})A_j(q + \Delta q_{(1)})\Delta q^n_{(2)}\right\} \Delta q_{(1)}^m + \Omicron((\Delta q)^3). \end{aligned}

ここで再び

\begin{aligned} A_l(q + \Delta q_{(1)}) &= A_l(q) + \frac{\partial A_l(q)}{\partial q^m} \Delta q_{(1)}^m + \frac{1}{2} \frac{\partial^2 A_l(q)}{\partial q^m \partial q^n} \Delta q^m_{(1)}\Delta q^n_{(1)} + \Omicron((\Delta q)^3)\\ \frac{\partial A_l(q + \Delta q_{(1)})}{\partial q^n} &= \frac{\partial A_l(q)}{\partial q^n} + \frac{\partial^2 A_l(q)}{\partial q^m \partial q^n}\Delta q^m_{(1)}+ \Omicron((\Delta q)^2)\\ \Gamma^{k}_{\,ln}(q + \Delta q_{(1)}) &= \Gamma^{k}_{\,ln}(q) + \frac{\partial \Gamma^{k}_{\,ln}(q)}{\partial q^m} \Delta q_{(1)}^m+ \Omicron((\Delta q)^2) \end{aligned}

を代入することで、

\begin{aligned} A_l(q + \Delta q_{(1)} &+ \Delta q_{(2)})_{//Q_I//P}\\ &=A_l(q) + \frac{\partial A_l(q)}{\partial q^n}(\Delta q^n_{(1)} + \Delta q^n_{(2)}) + \frac{\partial^2 A_l(q)}{\partial q^m \partial q^n} \Delta q^m_{(1)}\Delta q^n_{(2)}\\ &\qquad + \frac{1}{2} \frac{\partial^2 A_l(q)}{\partial q^n \partial q^m}\Delta q^n_{(2)}\Delta q^m_{(2)}+ \frac{1}{2} \frac{\partial^2 A_l(q)}{\partial q^n \partial q^m}\Delta q^n_{(1)}\Delta q^m_{(1)}\\ &\qquad - \Gamma^{k}_{\,ln}(q)A_k(q)\Delta q^n_{(2)} - \Gamma^{k}_{\,ln}(q)\frac{\partial A_l(q)}{\partial q^m} \Delta q^m_{(1)} \Delta q^n_{(2)} - \frac{\partial \Gamma^{k}_{\,ln}(q)}{\partial q^m}A_k(q)\Delta q^m_{(1)}\Delta q^n_{(2)}\\ &\qquad - \Gamma^{k}_{\,ln}(q)\frac{\partial A_k(q )}{\partial q^m} \Delta q^n_{(2)}\Delta q^m_{(2)}\\ &\qquad - \Gamma^k_{\,lm}(q)A_k(q)\Delta q_{(1)}^m - \Gamma^k_{\,lm}(q)\frac{\partial A_k(q)}{\partial q^n} \Delta q_{(1)}^n \Delta q_{(1)}^m - \Gamma^k_{\,lm}(q)\frac{\partial A_k(q)}{\partial q^n} \Delta q_{(2)}^n \Delta q_{(1)}^m\\ &\qquad + \Gamma^k_{\,lm}(q) \Gamma^{j}_{\,kn}(q)A_j(q ) \Delta q_{(2)}^n \Delta q_{(1)}^m + \Omicron((\Delta q)^3)\\ &=A_l(q) + \frac{\partial A_l(q)}{\partial q^n}(\Delta q^n_{(1)} + \Delta q^n_{(2)}) - \Gamma^{k}_{\,lm}(q)A_k(q)(\Delta q^m_{(1)} + \Delta q^m_{(2)})\\ &\qquad + \frac{\partial^2 A_l(q)}{\partial q^m \partial q^n} \Delta q^m_{(1)}\Delta q^n_{(2)}+ \frac{1}{2} \frac{\partial^2 A_l(q)}{\partial q^m \partial q^n}(\Delta q^m_{(1)}\Delta q^n_{(1)} + \Delta q^m_{(2)}\Delta q^n_{(2)})\\ &\qquad - \Gamma^{k}_{\,lm}(q)\frac{\partial A_k(q )}{\partial q^n} (\Delta q^m_{(1)}\Delta q^n_{(1)}+ \Delta q^m_{(2)}\Delta q^n_{(2)})\\ &\qquad - \Gamma^k_{\,lm}(q)\frac{\partial A_k(q)}{\partial q^n} (\Delta q_{(1)}^m \Delta q_{(2)}^n + \Delta q_{(2)}^m \Delta q_{(1)}^n)\\ &\qquad - \frac{\partial \Gamma^{k}_{\,ln}(q)}{\partial q^m}A_k(q)\Delta q^m_{(1)}\Delta q^n_{(2)}+ \Gamma^k_{\,lm}(q) \Gamma^{j}_{\,kn}(q)A_j(q ) \Delta q_{(2)}^n \Delta q_{(1)}^m\\ &\qquad+ \Omicron((\Delta q)^3)\\ \end{aligned}

同様の要領で、R \to Q_{II} \to P の経路についても計算してみる。

\begin{aligned} A_l(q + \Delta q_{(1)} &+ \Delta q_{(2)})_{//Q_{II}//P}\\ &=A_l(q) + \frac{\partial A_l(q)}{\partial q^n}(\Delta q^n_{(1)} + \Delta q^n_{(2)}) - \Gamma^{k}_{\,lm}(q)A_k(q)(\Delta q^m_{(1)} + \Delta q^m_{(2)})\\ &\qquad + \frac{\partial^2 A_l(q)}{\partial q^m \partial q^n} \Delta q^m_{(1)}\Delta q^n_{(2)}+ \frac{1}{2} \frac{\partial^2 A_l(q)}{\partial q^m \partial q^n}(\Delta q^m_{(1)}\Delta q^n_{(1)} + \Delta q^m_{(2)}\Delta q^n_{(2)})\\ &\qquad - \Gamma^{k}_{\,lm}(q)\frac{\partial A_k(q )}{\partial q^n} (\Delta q^m_{(1)}\Delta q^n_{(1)}+ \Delta q^m_{(2)}\Delta q^n_{(2)})\\ &\qquad - \Gamma^k_{\,lm}(q)\frac{\partial A_k(q)}{\partial q^n} (\Delta q_{(1)}^m \Delta q_{(2)}^n + \Delta q_{(2)}^m \Delta q_{(1)}^n)\\ &\qquad - \frac{\partial \Gamma^{k}_{\,ln}(q)}{\partial q^m}A_k(q)\Delta q^n_{(1)}\Delta q^m_{(2)}+ \Gamma^k_{\,lm}(q) \Gamma^{j}_{\,kn}(q)A_j(q ) \Delta q_{(2)}^m \Delta q_{(1)}^n\\ &\qquad+ \Omicron((\Delta q)^3). \end{aligned}

以上から、

\begin{aligned} A_l(q + &\Delta q_{(1)} + \Delta q_{(2)})_{//Q_I//P} - A_l(q + \Delta q_{(1)} + \Delta q_{(2)})_{//Q_{II}//P} \\ &= - \frac{\partial \Gamma^{k}_{\,ln}(q)}{\partial q^m}A_k(q)\Delta q^m_{(1)}\Delta q^n_{(2)}+ \Gamma^k_{\,lm}(q) \Gamma^{j}_{\,kn}(q)A_j(q ) \Delta q_{(2)}^n \Delta q_{(1)}^m\\ &\qquad + \frac{\partial \Gamma^{k}_{\,ln}(q)}{\partial q^m}A_k(q)\Delta q^n_{(1)}\Delta q^m_{(2)} - \Gamma^k_{\,lm}(q) \Gamma^{j}_{\,kn}(q)A_j(q ) \Delta q_{(2)}^m \Delta q_{(1)}^n + \Omicron((\Delta q)^3)\\ &= -\left\{ \frac{\partial \Gamma^k_{\,ln}(q)}{\partial q^m} - \frac{\partial \Gamma^k_{\,lm}(q)}{\partial q^n} + \Gamma^{k}_{\,jm}(q)\Gamma^{j}_{\,ln}(q) - \Gamma^{k}_{\,jn}(q)\Gamma^{j}_{\,lm}(q)\right\} A_k(q)\Delta q^m_{(1)}\Delta q^n_{(2)} + \Omicron((\Delta q)^3)\\ &= - R^{k}_{\,lmn} A_k(q) \Delta q^m_{(1)} \Delta q^n_{(2)} + \Omicron((\Delta q)^3) \end{aligned}

が示された。

参考文献

• 藤井保憲「時空と重力（物理学の回廊）」（産業図書、1979）
  https://amzn.asia/d/9SXmTCb