Zenn
Open5

KFAS による状態空間時系列モデリングの snippet 集

R
時系列解析
状態空間モデル
kfas
統計モデリング
畳屋民也畳屋民也

この Scrap は？

KFAS を用いた状態空間時系列モデルのモデル種類別のモデリング方法を解説する。

https://cran.r-project.org/web/packages/KFAS/index.html

状態空間時系列モデル（線形ガウス）の理論

以下を参照
https://tatamiya-practice.hatenablog.com/entry/2020/12/29/204451
https://tatamiya-practice.hatenablog.com/entry/2021/01/10/152509

状態空間時系列モデル（線形ガウス）の一般形

\begin{aligned} \boldsymbol{y}_t &= \boldsymbol{Z}_t \boldsymbol{\alpha}_t + \boldsymbol{\boldsymbol{\varepsilon}}_t, \quad \boldsymbol{\varepsilon}_t \sim N(\boldsymbol{0}, \boldsymbol{H}_t)\\ \boldsymbol{\alpha}_{t+1} &= \boldsymbol{T}_t \boldsymbol{\alpha}_t + \boldsymbol{R}_t \boldsymbol{\eta}_t, \quad \boldsymbol{\eta}_t \sim N(\boldsymbol{0}, \boldsymbol{Q}_t) \end{aligned}

サンプルデータの準備

set.seed(13)
x1 <- 100 + arima.sim(model=list(ar=0.999), n=100)

s <- 2.5 * sin(seq(0, 99, length.out=100) * 2 * pi / 4)
y <- 1.2 * x1 + s + rnorm(100)
y[71:100] <- y[71:100] + 10

time.points <- seq.Date(as.Date("2014-01-01"), by=1, length.out=100)
datetime_cp <- time.points[71]

data <- data.frame(day=time.points, y=y, x1=x1) %>%
  mutate(flg_interfere = case_when(day>=datetime_cp~1, .default = 0)) 

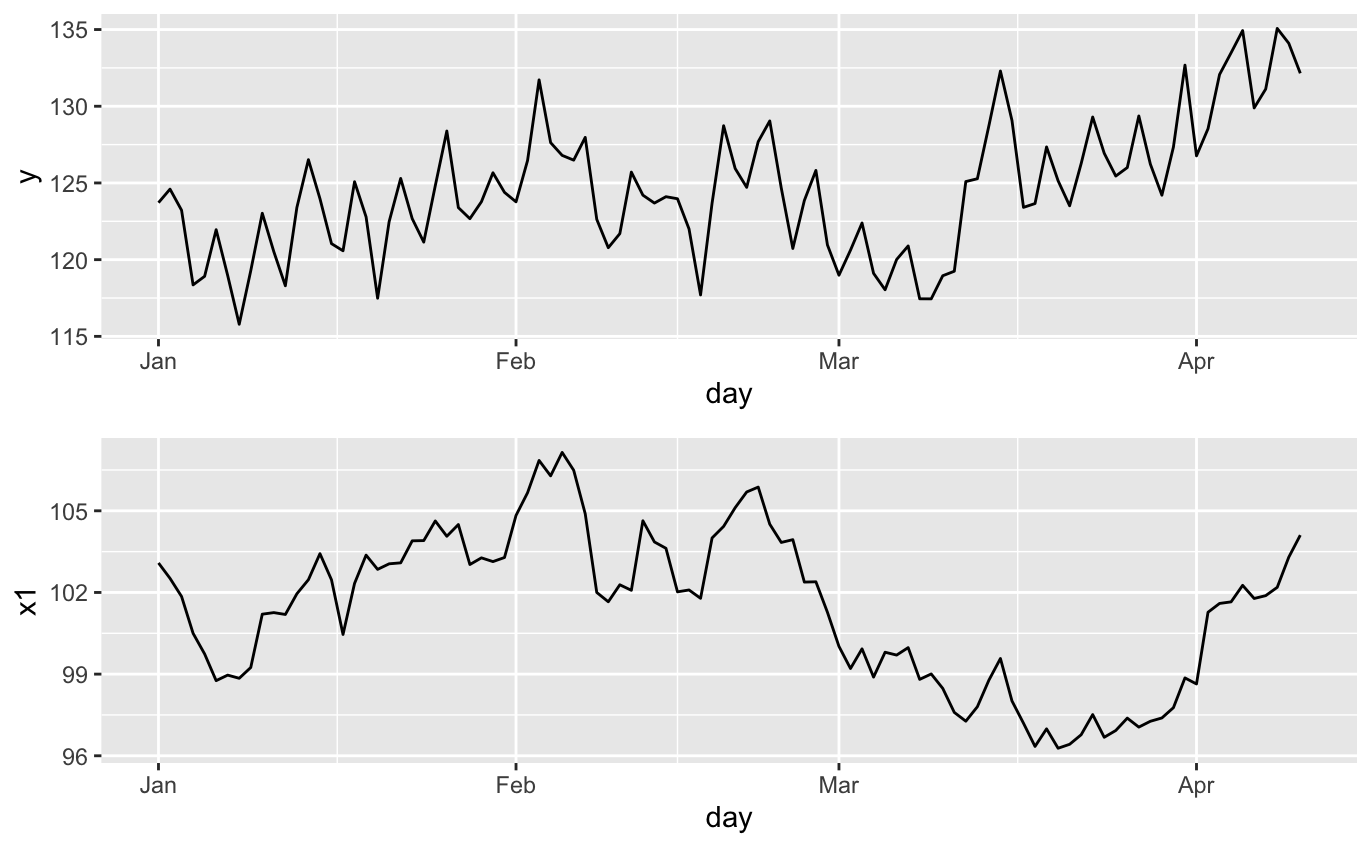
p1 <- ggplot(data=data) +
  geom_line(aes(x=day, y=y))

p2 <- ggplot(data=data) +
  geom_line(aes(x=day, y=x1))

grid.arrange(p1, p2)

実行コード

https://github.com/tatamiya/blog_artifacts/blob/main/zenn/20231028_kfas/kfas_guide.Rmd

畳屋民也畳屋民也

ローカルレベルモデル

\begin{aligned} y_t &= \mu_t + \varepsilon_t, \quad \varepsilon_t \sim N(0, \sigma_\varepsilon^2)\\ \mu_{t+1} &= \mu_t + \eta_t, \quad \eta_t \sim N(0, \sigma_\eta^2) \end{aligned}

KFAS によるモデリング

model_ll <- SSModel(y ~ SSMtrend(degree = 1, Q = NA),
                 data=data, H=NA)

fit_ll <- fitSSM(model_ll, numeric(2), method="BFGS")

全成分

P(y_t \vert y_{1:T}) 
pred_all <- predict(fit_ll$model, states="all", interval="prediction", level=0.95)

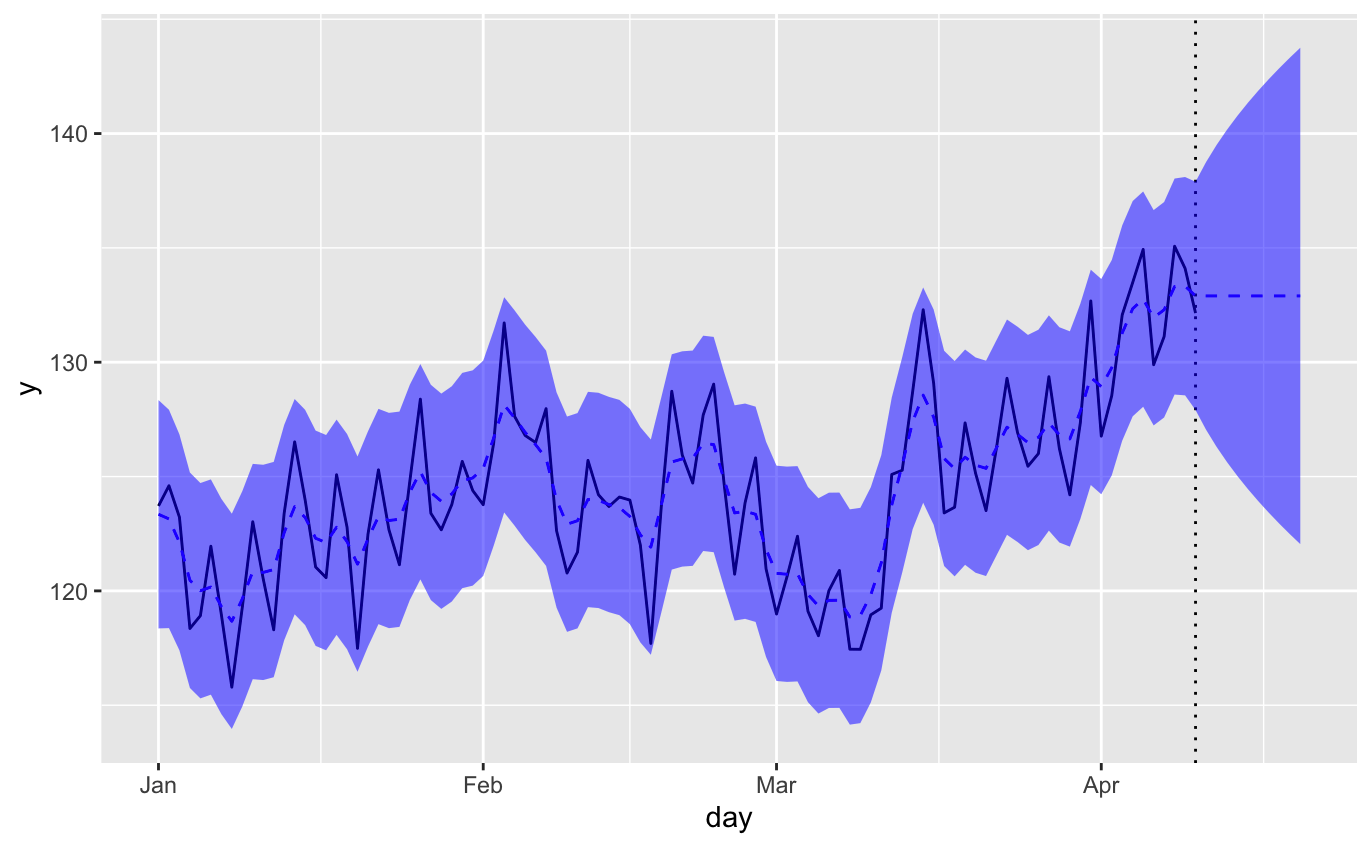
トレンド成分

P(\mu_t \vert y_{1:T}) 
pred_trend <- predict(fit_ll$model, states="trend", interval="confidence", level=0.95)

畳屋民也畳屋民也

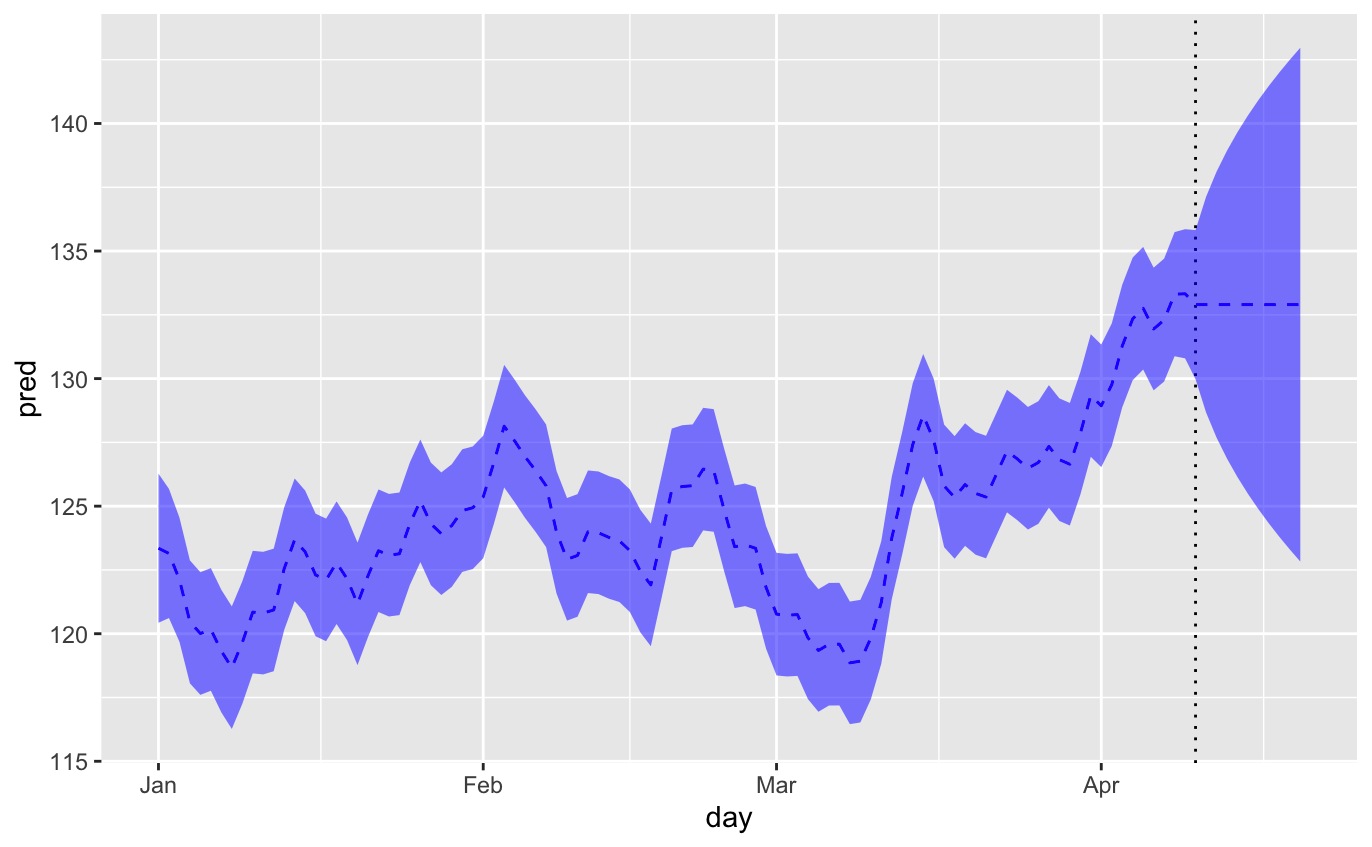
平滑化トレンドモデル

\begin{aligned} y_t &= \mu_t + \varepsilon_t, \quad \varepsilon_t \sim N(0, \sigma_\varepsilon^2)\\ \mu_{t+1} &= \mu_t + \delta_t\\ \delta_{t+1} &= \delta_t + \zeta_t, \quad \zeta_t \sim N(0, \sigma_\zeta^2) \end{aligned}

もしくは、

\begin{aligned} y_t = (1, 0) \begin{pmatrix} \mu_t\\ \delta_t \end{pmatrix} + \varepsilon_t, \quad \varepsilon_t \sim N(0, \sigma_\varepsilon^2)\\ \begin{pmatrix} \mu_{t+1}\\ \delta_{t+1} \end{pmatrix} = \begin{pmatrix} 1 & 1\\ 0 & 1 \end{pmatrix} \begin{pmatrix} \mu_{t}\\ \delta_{t} \end{pmatrix} + \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix} \boldsymbol{\zeta}_t\\ \boldsymbol{\zeta}_t \sim N\left( \begin{pmatrix} 0\\ 0 \end{pmatrix}, \begin{pmatrix} 0 & 0\\ 0 & \sigma_\zeta^2 \end{pmatrix} \right) \end{aligned}

モデリング

model_st <- SSModel(y ~ SSMtrend(degree = 2, Q = c(list(0), list(NA))),
                 data=data, H=NA)

fit_st <- fitSSM(model_st, numeric(2), method="BFGS")

モデルパラメータ

\boldsymbol{Z} = (1,0) 
model_st$Z

## , , 1
## 
##      level slope
## [1,]     1     0
\boldsymbol{T} = \begin{pmatrix} 1 & 1\\ 0 & 1 \end{pmatrix} 
model_st$T

## , , 1
## 
##       level slope
## level     1     1
## slope     0     1
\boldsymbol{R} = \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix} 
model_st$R

## , , 1
## 
##       [,1] [,2]
## level    1    0
## slope    0    1

推定パラメータ

\boldsymbol{H}=\sigma_\varepsilon^2 
fit_st$model$H

## , , 1
## 
##          [,1]
## [1,] 6.471462
\boldsymbol{Q} = \begin{pmatrix} 0 & 0\\ 0 & \sigma_\zeta^2 \end{pmatrix} 
fit_st$model$Q

## , , 1
## 
##      [,1]       [,2]
## [1,]    0 0.00000000
## [2,]    0 0.09705671

結果

全成分

P(y_t \vert y_{1:T}) 
pred_all <- predict(fit_st$model, states="all", interval="prediction", level=0.95)

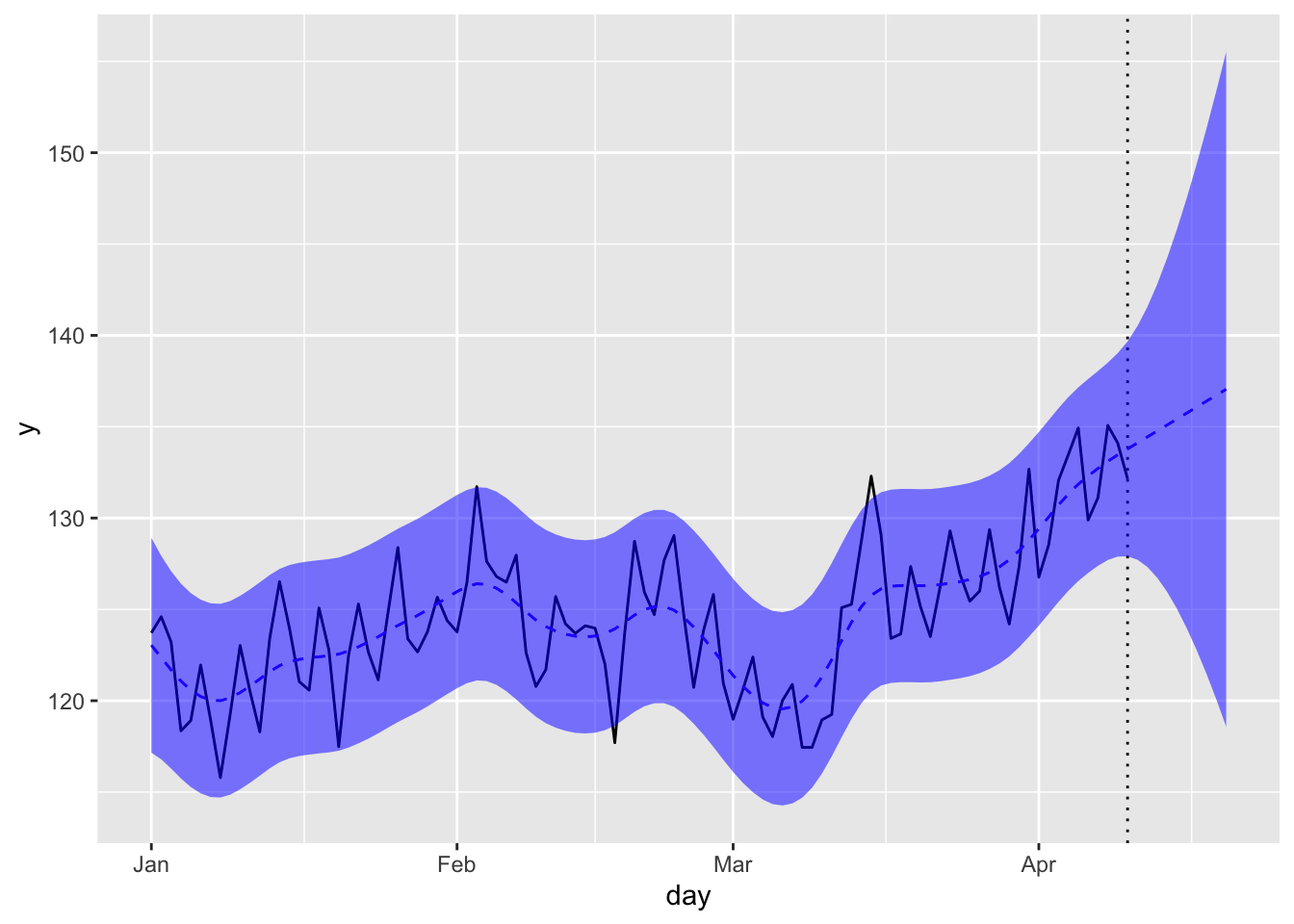
トレンド成分

P(\mu_t \vert y_{1:T}) 
pred_slope <- predict(fit_st$model, states="trend", interval="confidence", level=0.95)

傾き成分

P(\delta_t \vert y_{1:T}) 
pred_trend <- predict(fit_st$model, states="slope", interval="confidence", level=0.95)

畳屋民也畳屋民也

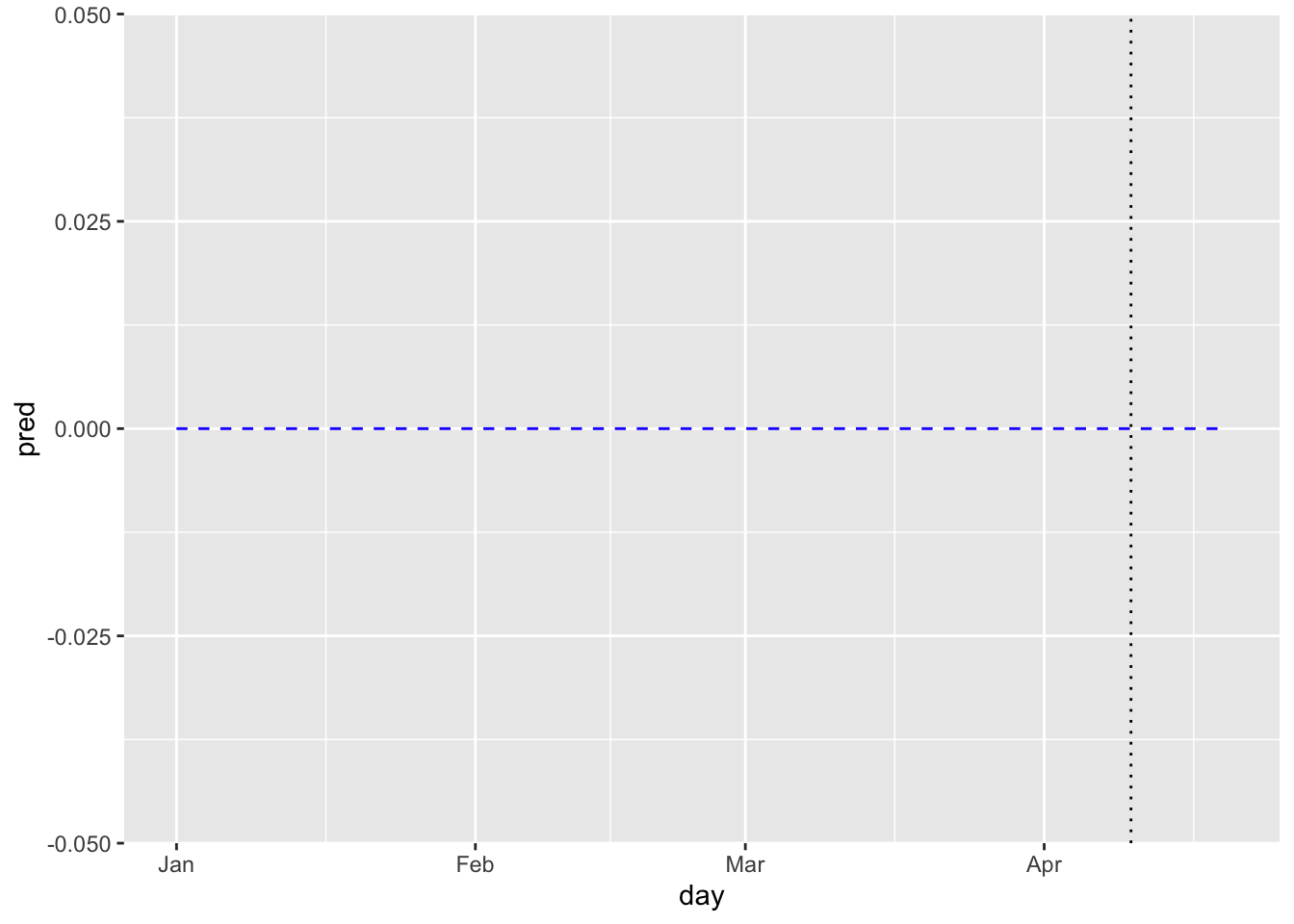
ローカル線形トレンドモデル

\begin{aligned} y_t &= \mu_t + \varepsilon_t, \quad \varepsilon_t \sim N(0, \sigma_\varepsilon^2)\\ \mu_{t+1} &= \mu_t + \delta_t + w_t, \quad w_t \sim N(0, \sigma_w^2) \\ \delta_{t+1} &= \delta_t + \zeta_t, \quad \zeta_t \sim N(0, \sigma_\zeta^2) \end{aligned}
\begin{aligned} y_t = (1, 0) \begin{pmatrix} \mu_t\\ \delta_t \end{pmatrix} + \varepsilon_t, \quad \varepsilon_t \sim N(0, \sigma_\varepsilon^2)\\ \begin{pmatrix} \mu_{t+1}\\ \delta_{t+1} \end{pmatrix} = \begin{pmatrix} 1 & 1\\ 0 & 1 \end{pmatrix} \begin{pmatrix} \mu_{t}\\ \delta_{t} \end{pmatrix} + \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix} \begin{pmatrix} w_t\\ \zeta_t \end{pmatrix} \\ \begin{pmatrix} w_t\\ \zeta_t \end{pmatrix} \sim N\left( \begin{pmatrix} 0\\ 0 \end{pmatrix}, \begin{pmatrix} \sigma_w^2 & 0\\ 0 & \sigma_\zeta^2 \end{pmatrix} \right) \end{aligned}

モデリング

model_lt <- SSModel(y ~ SSMtrend(degree = 2, Q = c(list(NA), list(NA))),
                 data=data, H=NA)

fit_lt <- fitSSM(model_lt, numeric(3), method="BFGS")

モデルパラメータ

\boldsymbol{Z} = (1,0) 
model_lt$Z

## , , 1
## 
##      level slope
## [1,]     1     0
\boldsymbol{T} = \begin{pmatrix} 1 & 1\\ 0 & 1 \end{pmatrix} 
model_lt$T

## , , 1
## 
##       level slope
## level     1     1
## slope     0     1
\boldsymbol{R} = \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix} 
model_lt$R

## , , 1
## 
##       [,1] [,2]
## level    1    0
## slope    0    1

推定パラメータ

\boldsymbol{H}=\sigma_\varepsilon^2 
fit_lt$model$H

## , , 1
## 
##         [,1]
## [1,] 4.15144
\boldsymbol{Q} = \begin{pmatrix} \sigma_w^2 & 0\\ 0 & \sigma_\zeta^2 \end{pmatrix} 
fit_lt$model$Q

## , , 1
## 
##         [,1]         [,2]
## [1,] 2.58792 0.000000e+00
## [2,] 0.00000 9.878334e-06

結果

全成分

P(y_t \vert y_{1:T}) 
pred_all <- predict(fit_lt$model, states="all", interval="prediction", level=0.95)

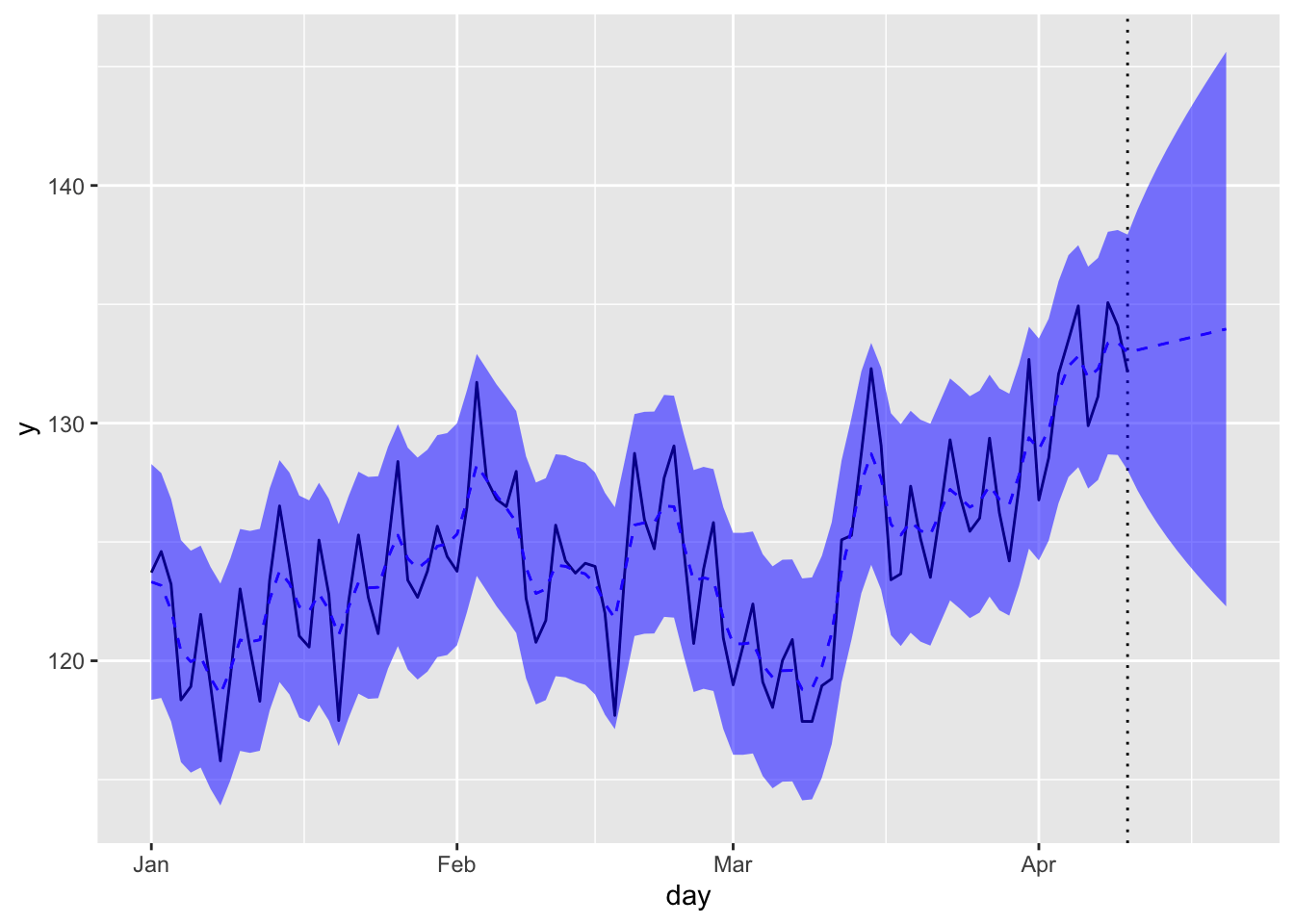
トレンド成分

P(\mu_t \vert y_{1:T}) 
pred_trend <- predict(fit_lt$model, states="trend", interval="confidence", level=0.95)

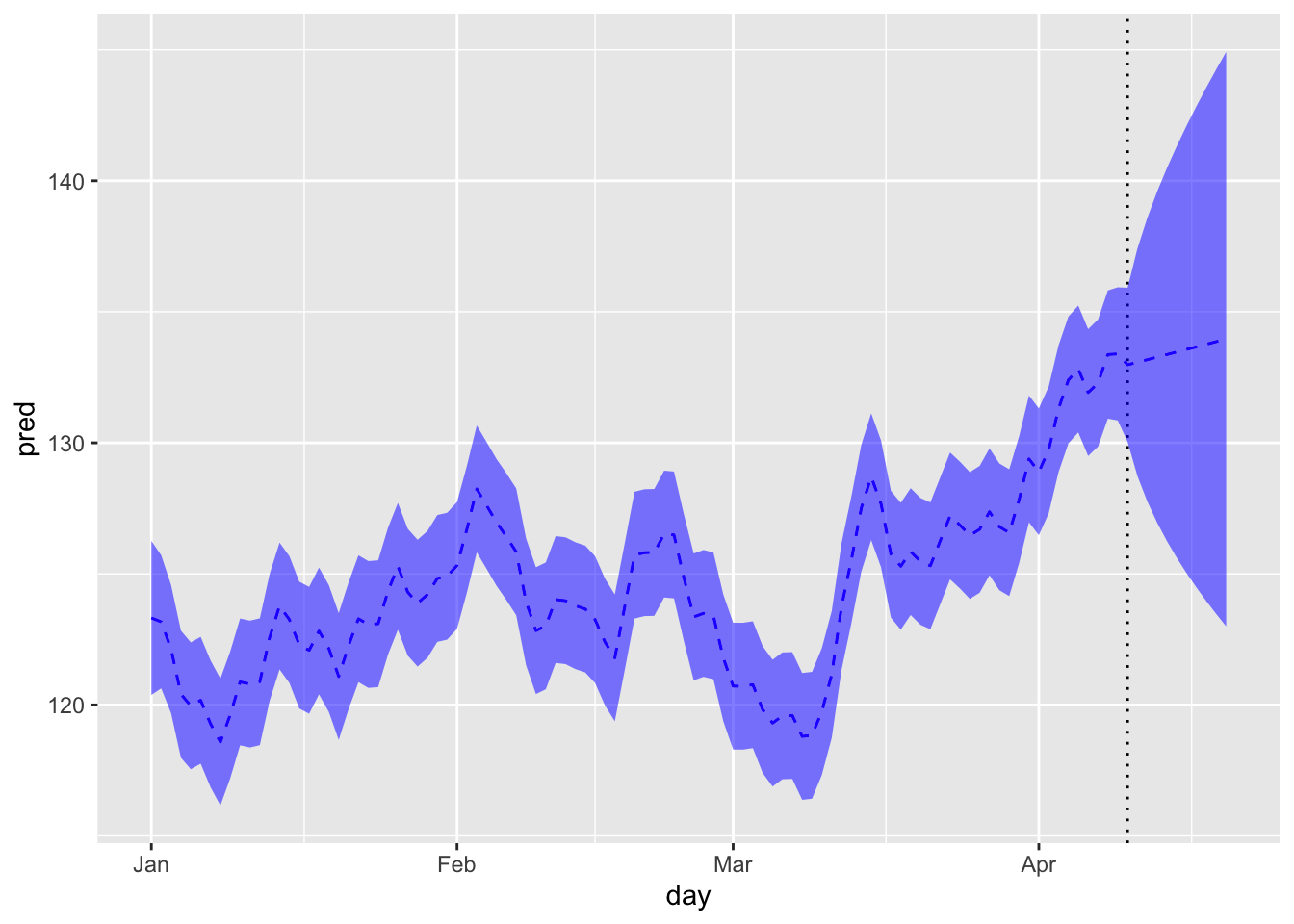
傾き成分

P(\delta_t \vert y_{1:T}) 
pred_slope <- predict(fit_lt$model, states="slope", interval="confidence", level=0.95)

畳屋民也畳屋民也

季節成分 + ローカルレベルモデル

\begin{aligned} y_t &= \mu_t + \gamma_t + \varepsilon_t, \quad \varepsilon_t \sim N(0, \sigma_\varepsilon^2)\\ \mu_{t+1} &= \mu_t + \eta^{(\mu)}_t, \quad \eta^{(\mu)}_t \sim N(0, \sigma_\mu^2) \\ \gamma_{t+1} &= -\sum_{i=0}^{s-2} \gamma_{t-i} + \eta^{(\gamma)}_t, \quad \eta^{(\gamma)}_t \sim N(0, \sigma_\gamma^2) \end{aligned}

または、

\begin{aligned} y_t = (1, 1, 0, 0, \cdots, 0) \begin{pmatrix} \mu_{t}\\ \gamma_{t}\\ \gamma_{t-1}\\ \gamma_{t-2}\\ \vdots\\ \gamma_{t-s+2} \end{pmatrix} + \varepsilon_t, \quad \varepsilon_t \sim N(0, \sigma_\varepsilon^2)\\ \begin{pmatrix} \mu_{t+1}\\ \gamma_{t+1}\\ \gamma_t\\ \gamma_{t-1}\\ \vdots\\ \gamma_{t-s+3} \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 & 0 & \cdots & 0 & 0\\ 0 & -1 & -1 & -1 & \cdots & -1 & -1\\ 0 & 1 & 0 & 0 &\cdots & 0 & 0\\ 0 & 0 & 1 & 0 &\cdots & 0 &0\\ \vdots & \vdots & \vdots & \cdots & \vdots & \vdots\\ 0 & 0 & 0 & 0 &\cdots & 1 & 0\\ \end{pmatrix} \begin{pmatrix} \mu_{t}\\ \gamma_{t}\\ \gamma_{t-1}\\ \gamma_{t-2}\\ \vdots\\ \gamma_{t-s+2} \end{pmatrix} + \begin{pmatrix} 1 & 0\\ 0 & 1\\ 0 & 0\\ 0 & 0\\ \vdots & \vdots\\ 0 & 0 \end{pmatrix} \begin{pmatrix} \eta^{(\mu)}_t\\ \eta^{(\gamma)}_t \end{pmatrix} \\ \begin{pmatrix} \eta^{(\mu)}_t\\ \eta^{(\gamma)}_t \end{pmatrix} \sim N\left( \begin{pmatrix} 0\\ 0 \end{pmatrix}, \begin{pmatrix} \sigma_\mu^2 & 0\\ 0 & \sigma_\gamma^2 \end{pmatrix} \right) \end{aligned}

モデリング

model_s_ll <- SSModel(y ~ SSMtrend(degree = 1, Q = NA)
                    + SSMseasonal(period=4, sea.type="dummy", Q=NA),
                 data=data, H=NA)

fit_s_ll <- fitSSM(model_s_ll, numeric(3), method="BFGS")

モデルパラメータ

\boldsymbol{Z} = (1,1,0, 0, ..., 0) 
model_s_ll$Z
## , , 1
## 
##      level sea_dummy1 sea_dummy2 sea_dummy3
## [1,]     1          1          0          0
\boldsymbol{T} = \begin{pmatrix} 1 & 0 & 0 & 0 & \cdots & 0 & 0\\ 0 & -1 & -1 & -1 & \cdots & -1 & -1\\ 0 & 1 & 0 & 0 &\cdots & 0 & 0\\ 0 & 0 & 1 & 0 &\cdots & 0 &0\\ \vdots & \vdots & \vdots & \cdots & \vdots & \vdots\\ 0 & 0 & 0 & 0 &\cdots & 1 & 0\\ \end{pmatrix} 
model_s_ll$T
## , , 1
## 
##            level sea_dummy1 sea_dummy2 sea_dummy3
## level          1          0          0          0
## sea_dummy1     0         -1         -1         -1
## sea_dummy2     0          1          0          0
## sea_dummy3     0          0          1          0
\boldsymbol{R} = \begin{pmatrix} 1 & 0\\ 0 & 1\\ 0 & 0\\ 0 & 0\\ \vdots & \vdots\\ 0 & 0 \end{pmatrix} 
model_s_ll$R
## , , 1
## 
##            [,1] [,2]
## level         1    0
## sea_dummy1    0    1
## sea_dummy2    0    0
## sea_dummy3    0    0

推定パラメータ

\boldsymbol{H}=\sigma_\varepsilon^2 
fit_s_ll$model$H
## , , 1
## 
##              [,1]
## [1,] 0.0006470018
\boldsymbol{Q} = \begin{pmatrix} \sigma_\mu^2 & 0\\ 0 & \sigma_\gamma^2 \end{pmatrix} 
fit_s_ll$model$Q
## , , 1
## 
##          [,1]         [,2]
## [1,] 3.606111 0.000000e+00
## [2,] 0.000000 6.535295e-07

結果

全成分

P(y_t \vert y_{1:T}) 
pred_all <- predict(fit_s_ll$model, states="all", interval="prediction", level=0.95)

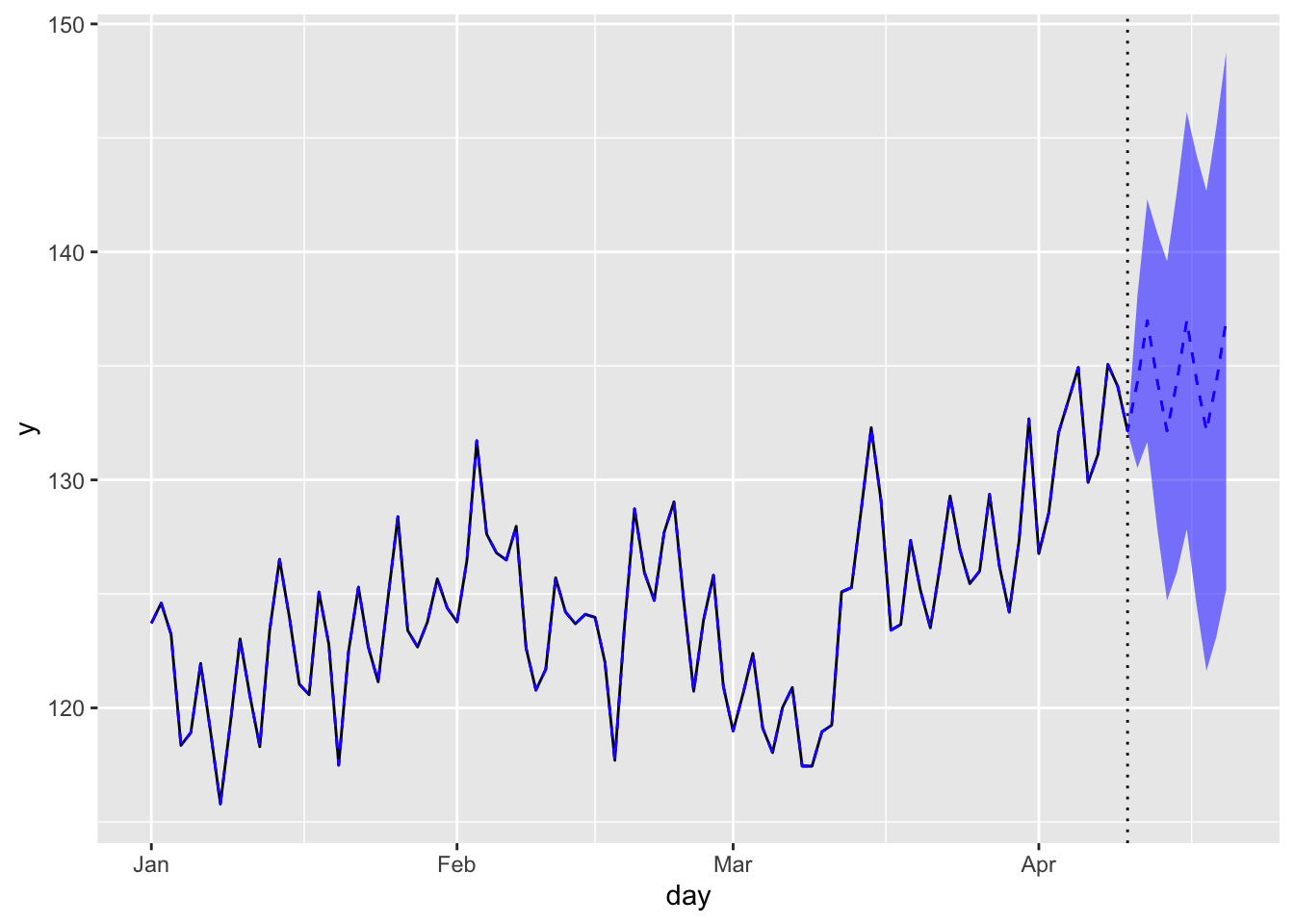
トレンド成分

P(\mu_t \vert y_{1:T}) 
pred_all <- predict(fit_s_ll$model, states="trend", interval="confidence", level=0.95)

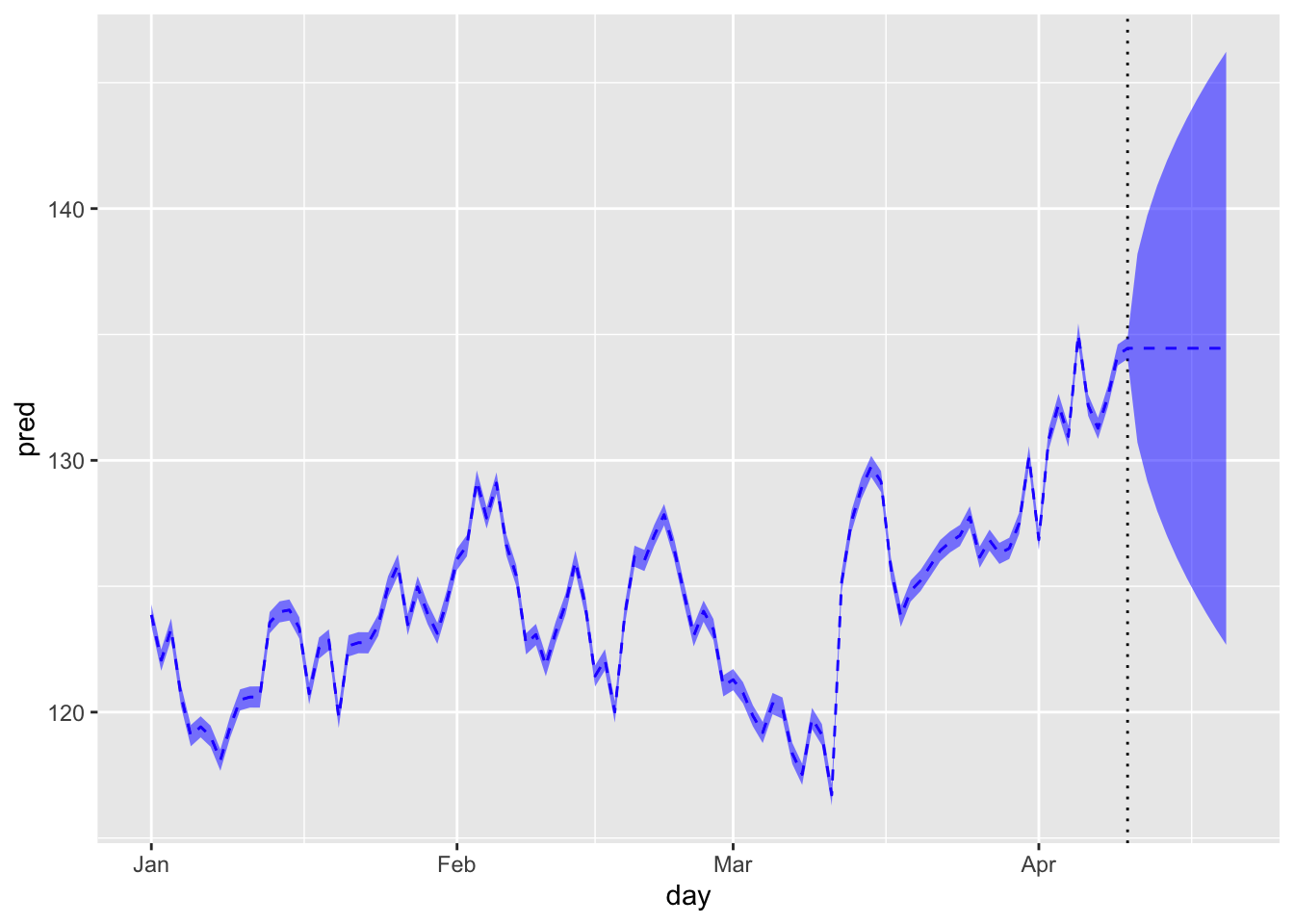
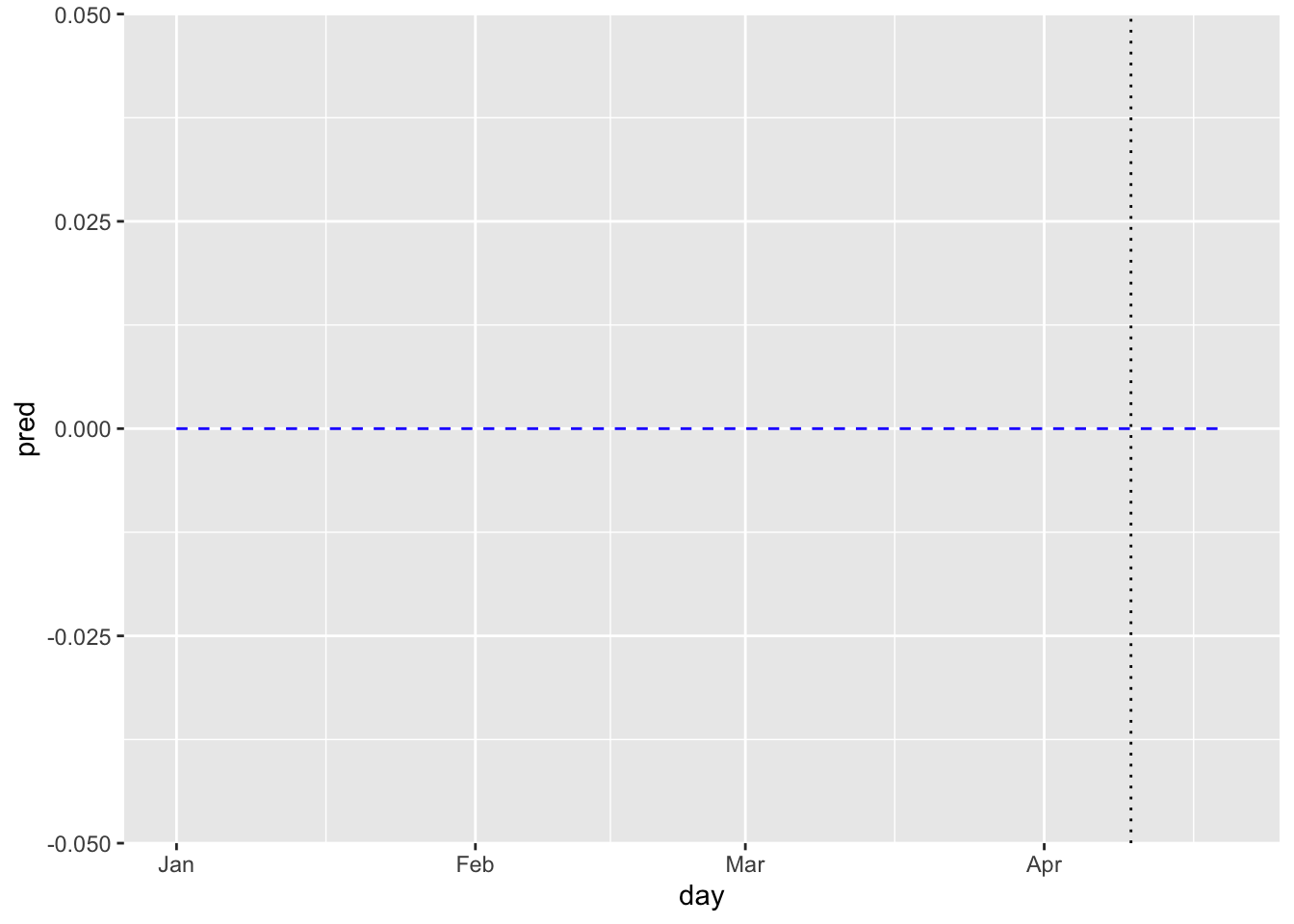
季節成分

P(\gamma_t \vert y_{1:T}) 
pred_all <- predict(fit_s_ll$model, states="seasonal", interval="confidence", level=0.95)