コピュラとその周辺の話(順位相関)
順位相関
順位相関とはデータ値の大きさの順序関係をもとにデータの相関を定量化したものであり、データセット
順位相関にはスピアマンとケンドールの2種類がある。
スピアマンの順位相関
求め方
データセット
この時、スピアマンの順位相関は以下のように
式変形
これらを用いると、
従って分子は
次に、分母を求める。
ここで、
を用いて
が成り立つ。
途中で
以上から、
理論的な表現
ここで、
なお、
コピュラを用いた表現
先ほどの
これを用いることで、
その他の表現方法
ケンドールの順位相関
求め方
ケンドールの順位相関は以下のように求める:
1行目から2行目の式変換では、
【
簡単のため、
このとき
同様に、
【具体的な計算例】
例として、
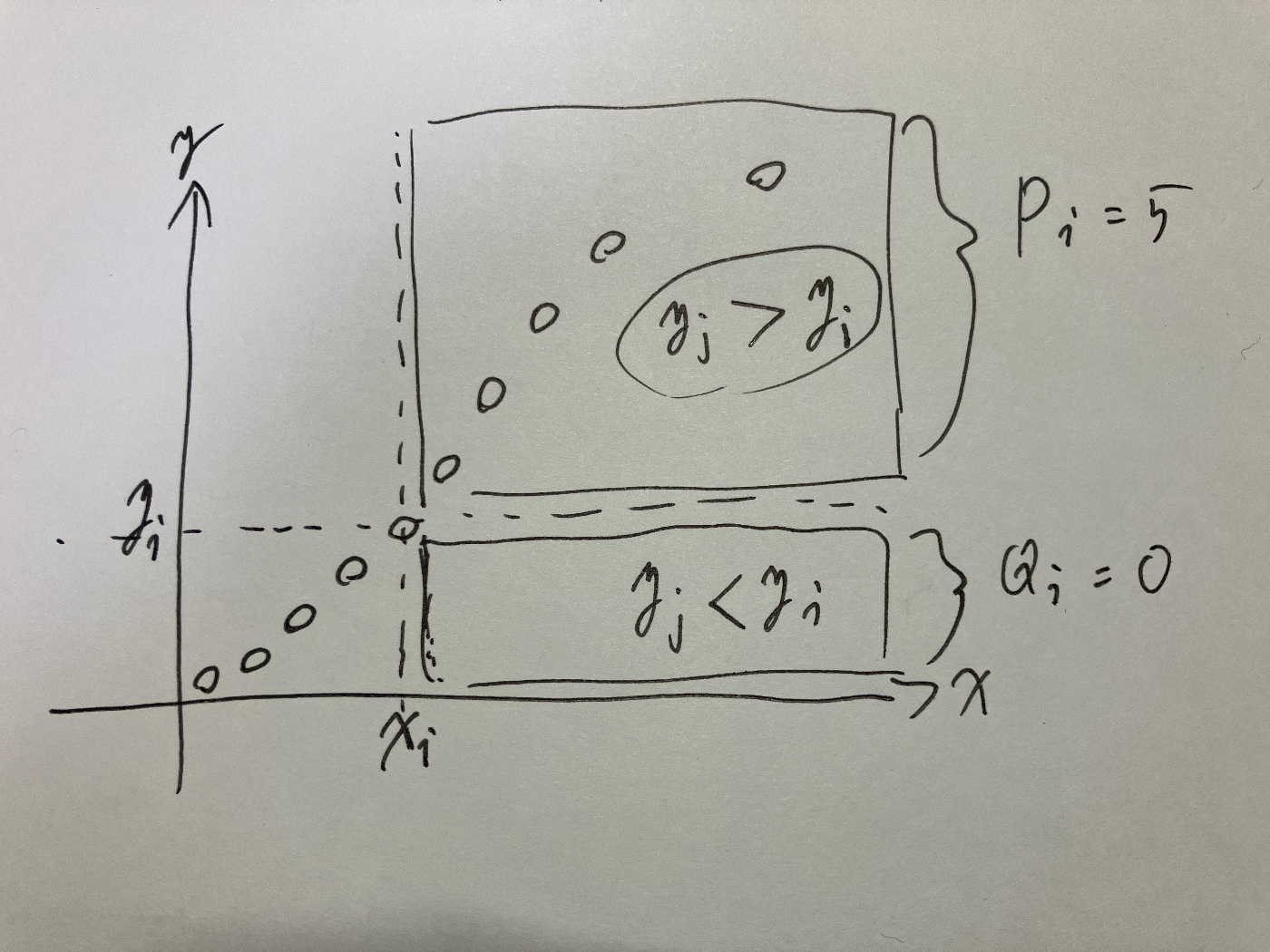
上記は
このような方法で
より、
となる。
逆に、
一方で、
この場合、
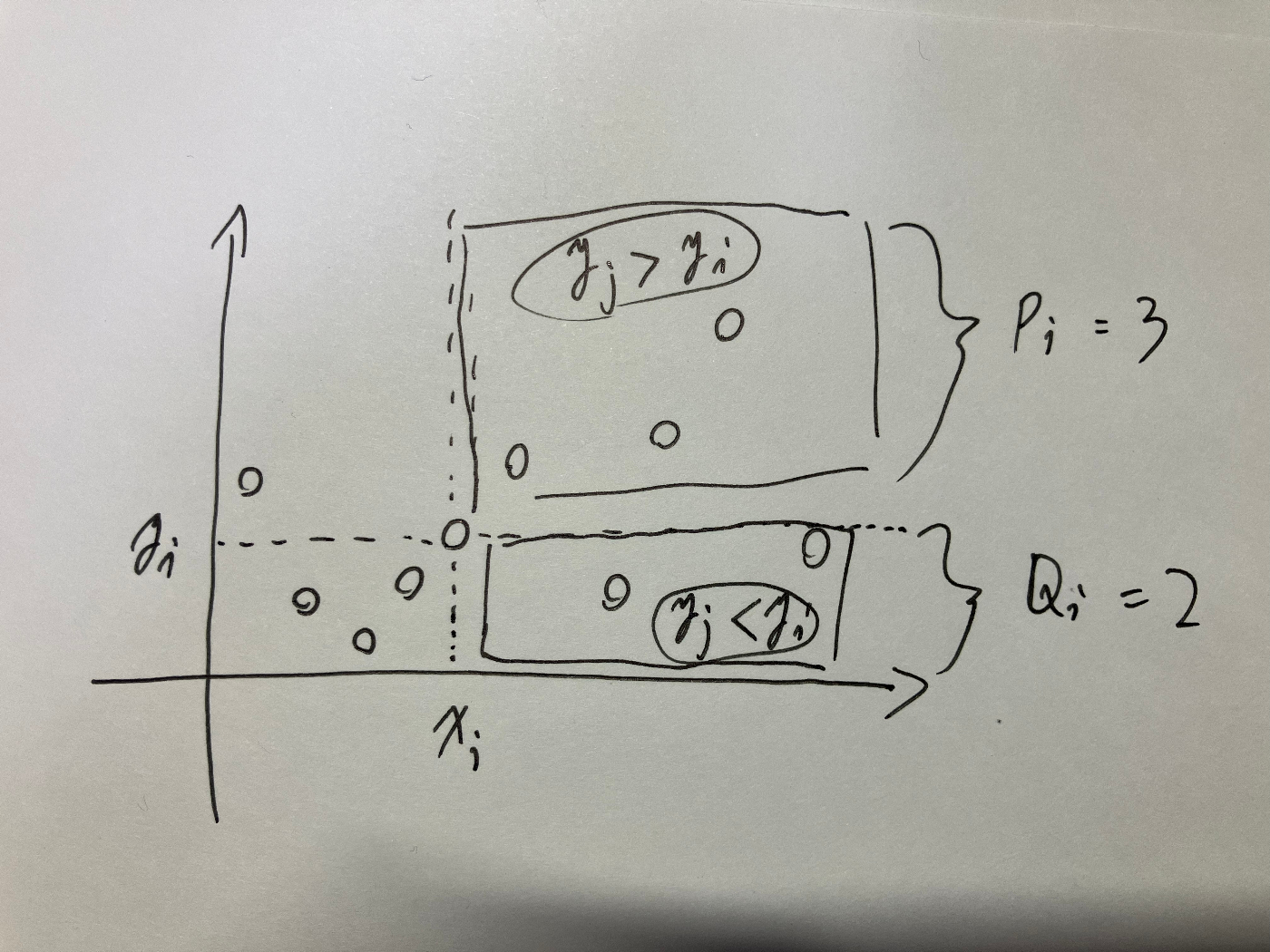
上記の例では、
このケースについても
であることから、
が得られる。
理論的な表現
ケンドールの順位相関係数は、理論的には以下のように定義される:
これは、(
例えば
従ってこのとき
【
なお、先ほどの
以下、
コピュラを用いた表現
ケンドールの順位相関もコピュラ
参考文献
江村 剛志、コピュラ理論の基礎(シリーズ 情報科学における確率モデル 12)、コロナ社 (2025)
上田 拓治、44の例題で学ぶ統計的検定と推定の解き方、オーム社 (2009)
神永 正博・木下 勉、Rで学ぶ確率統計学 一変量統計編、内田老鶴圃 (2019)