ROS2: マンタ採餌最適化: Manta Ray Foraging Optimization(MRFO)のC++実装
海洋ロボコンをやってた人です。
今回は、2020年にEngineering Applications of Artificial Intelligenceで掲載された マンタ採餌最適化:Manta Ray Foraging Optimization(MRFO) についての概要から、C++、ROS2実装までを書いていこうと思います。
経緯としては、様々な群知能のアルゴリズムを調べていた時にMRFOを見つけてしまい、マンタと共に3年間を過ごしてきた身として学ばなければならないという使命感を持ち、こちらでまとめることにしました。
本記事では、MRFOの実装プログラムって、こんな感じで実装できるんだ!という認知を広げる、自分自身の備忘録としていますので、お役に立てば幸いです。
何か、間違っている箇所等あれば、お気軽にご教授いただけると嬉しく思います。
※2023/02/26追記: 本記事の「ROS2」表記、正しくは「ROS 2」です。
※また、各説明で必要なものは原著からの引用となりますので、ご了承ください。
マンタ採餌最適化(MRFO)をC++で実装する
マンタ採餌最適化:MRFOとは?
MRFOはマンタ(オニイトマキエイ)の連鎖採餌(chain foraging)、サイクロン採餌(cyclone foraging)、宙返り採餌(somersault foraging)の3つの採餌方法をアルゴリズムで提案した手法です。
MRFOは、ハイパーパラメータがほとんどなく、局所最適解をより少ない計算コストで求めることができる面で、工学分野での利用可能性が高いとされています。(詳しくは原著のベンチマークを参考にしてください。)
また、成熟したオスのマンタが、毎日5kgのプランクトンを食べることができ、プランクトンを見つけるのも得意だそうです。
chain foragingは、50匹以上のマンタが採餌を開始するときにマンタが次々と列を作り採餌を行う行動から発想を得ており、自身の前を進んでいるマンタが餌を取りこぼしたものを、後方の自分が餌を食べることで、効率よく採餌できるそうです。アルゴリズムではローカル検索能力に大きく貢献する行動になっています。
cyclone foragingは、プランクトン密度が高くなると数十匹のマンタが集まり、サイクロンのような螺旋を辿りつつ移動する行動から発想を得ており、クジラ最適化アルゴリズム:The Whale Optimization Algorithm(WOA)と似たモデルとなっています。アルゴリズムではグローバル検索能力に大きく貢献する行動となっています。
somersault foragingは、マンタが餌を見つけると、プランクトンの周りを一周して自身に引き寄せるよう宙返りをする行動から発想を得ており、自然界ではまれに見られる採餌行動となっています。アルゴリズムではローカル検索能力を高め、収束率を上げることに貢献する行動となっています。
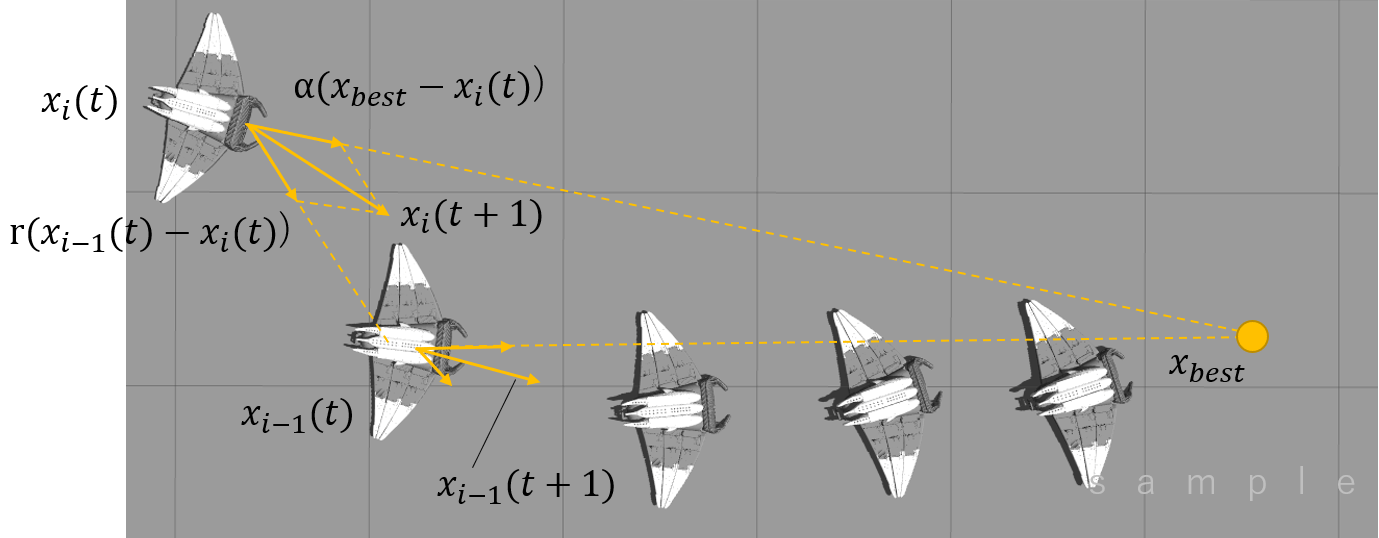
chain, cyclone, somersaultの3つの採餌行動を数理化したものが下記になります。
chain foraging
マンタは高濃度のプランクトンを見つけると、チェーンのような列を作り、前方の個体や目的のプランクトンの位置などへランダムに移動します。移動後、その個体が持つ自己ベスト位置は更新されます。
ある個体の位置は
となります。
ここで、
図で見てみる、
cyclone foraging
プランクトンを見つけると、螺旋を描きつつ餌に向かって動きます。マンタの場合は螺旋状に移動するだけでなく前方のマンタに向かっても泳ぐので、このことを考慮して数理モデルを定義します。
ここで、
このメカニズムにおいて、より広範囲なグローバル探索を実現できるようにする場合、探索空間で作製されたランダムな位置
ここで、

somersault foraging
宙返りでの採餌は、餌の位置が宙返りの回転軸とみなされ、各マンタは餌の周りを前後に泳ぎつつ、新しい位置へ宙返りしていきます。また、新しい位置へ宙返りを行う際に、ローカルベスト位置があれば更新していき、それを数理モデルで表すと以下のように表せます。
ここでSはマンタの宙返りの範囲を決める係数で
右辺の2項目を見ると、グローバルベスト位置と各マンタとの距離が減少するにつれて、現在の位置

MRFOのC++実装例
ざっくり数理モデルを把握したら、MRFOの疑似コードをもとにC++でプログラムを実装していきます。
WHILE stop criterion is not satisfied do
FOR i=1 TO N DO
IF rand < 0.5 THEN //Cyclone foraging
IF t/Tmax < rand THEN
xrand = xl + rand・(xu - xl)
If i=1
xi(t+1) = xrand + r(xrand - xi(t)) + β(xrand - xi(t))
ELSE // i = 2, ... , N
xi(t+1) = xrand + r(x(i-1)- xi(t)) + β(xrand - xi(t))
END IF.
ELSE
If i=1
xi(t+1) = xbest + r(xbest - xi(t)) + β(xbest - xi(t))
ELSE // i = 2, ... , N
xi(t+1) = xbest + r(x(i-1)- xi(t)) + β(xbest - xi(t))
END IF.
END IF.
ELSE // Chain foraging
If i=1
xi(t+1) = xi(t) + r(xbest - xi(t)) + α(xbest - xi(t))
ELSE // i = 2, ... , N
xi(t+1) = xi(t) + r(x(i-1)- xi(t)) + α(xbest - xi(t))
END IF.
Compute the fitness of each individual f(xi(t+1)). IF f(xi(t+1)) < f(xbest)
THEN xbest = xi(t+1)
// Somersault foraging
FOR i=1 TO N DO
xi(t+1) = xi(t) + S(r2*xbest - r3*xi(t))
Compute the fitness of each individual f(xi(t+1)). IF f(xi(t+1)) < f(xbest)
THEN xbest = xi(t+1)
END FOR.
END WHILE.
Return the best solution found so far xbest.
疑似コード見ても最初は良くわからないので、ブロック図で表すとこんな感じです。
以上を参考にC++でプログラムを実装すると、下記のようになります。
#include <stdlib.h>
#include<stdio.h>
#include <time.h>
#include <cfloat>
#include <cmath>
class Mrfo{
public:
Mrfo();
~Mrfo();
void move(int current_iter, int max_iter);
struct manta_ray{
double *position_ = nullptr;
double value;
};
struct manta_ray *manta; //Declarations that use pointers in structures
double *global_best_pos = nullptr;
double global_best_value = DBL_MIN;
int gbest_num;
private:
void evaluate(int population);
int dimension_ = 2; // MantaRays dimensions = number of solutions
double xminj = -1;
double xmaxj = 1;
int population_n = 30; // the size of plankton population 餌の数
int max_iter = 5; // maximum number of iterations 反復回数
double rand_select_foraging;
double coef;
double cutoff_rand, r, r1, r2, r3, xrand;
double alpha, beta;
const int s = 2; // somersault factor that decides the somersault range of matna rays
};
Mrfo::Mrfo()
{
// Initialize the manta ray
manta = new manta_ray[population_n];
for (int i=0; i<population_n; i++){
manta[i].position_ = new double[dimension_];
for (int j=0; j<dimension_; j++){
manta[i].position_[j] = xminj + (xmaxj - xminj) * ((double)rand() / RAND_MAX);
}
this->evaluate(i);
}
// Initialize global best pos and value
global_best_pos = new double[dimension_];
gbest_num = 0;
for (int i=0; i<population_n; i++){
if(manta[i].value < manta[gbest_num].value){
gbest_num = i;
}
}
global_best_value = manta[gbest_num].value;
for (int j=0; j<dimension_; j++){
global_best_pos[j] = manta[gbest_num].position_[j];
}
}
Mrfo::~Mrfo()
{
delete [] manta->position_;
delete [] global_best_pos;
}
void Mrfo::evaluate(int population){
double A = manta[population].position_[0];
double B = manta[population].position_[1];
manta[population].value = A*A + B*B;
}
void Mrfo::move(int current_iter, int max_iter)
{
for (int i=0; i < population_n; i++){
// Cyclone Foraging
rand_select_foraging = ((double)rand() / RAND_MAX);
if (rand_select_foraging < 0.5){
// printf("Cyclone:");
coef = double(current_iter)/double(max_iter);
cutoff_rand = ((double)rand() / RAND_MAX);
r = ((double)rand() / RAND_MAX);
r1 = ((double)rand() / RAND_MAX);
beta = 2 * std::exp(r1*(max_iter - current_iter + 1) / max_iter) * sin(2 * M_PI * r1);
if (coef < cutoff_rand){
// printf("cutoff\n");
xrand = xminj + (xmaxj - xminj) * ((double)rand() / RAND_MAX);
for (int j=0; j<dimension_; j++){
if(i == 0){
manta[i].position_[j] = xrand
+ r * (xrand - manta[i].position_[j])
+ beta * (xrand - manta[i].position_[j]);
}
else{ // population = 2 - N
manta[i].position_[j] = xrand
+ r * (manta[i-1].position_[j] - manta[i].position_[j])
+ beta * (xrand - manta[i].position_[j]);
}
}
}
else{
// printf("normal\n");
for (int j=0; j<dimension_; j++){
if(i == 0){
manta[i].position_[j] = global_best_pos[j]
+ r * (global_best_pos[j] - manta[i].position_[j])
+ beta * (global_best_pos[j] - manta[i].position_[j]);
}
else{ // population = 2 - N
manta[i].position_[j] = global_best_pos[j]
+ r * (manta[i-1].position_[j] - manta[i].position_[j])
+ beta * (global_best_pos[j] - manta[i].position_[j]);
}
}
}
}
// Chain Foraging
else{
// printf("Chain\n");
r = ((double)rand() / RAND_MAX);
alpha = 2 * r * (sqrt(fabs(log(r))));
for (int j=0; j<dimension_; j++){
if(i == 0){
manta[i].position_[j] = manta[i].position_[j]
+ r * (global_best_pos[j] - manta[i].position_[j])
+ alpha * (global_best_pos[j] - manta[i].position_[j]);
}
else{ // population = 2 - N
manta[i].position_[j] = manta[i].position_[j]
+ r * (manta[i-1].position_[j] - manta[i].position_[j])
+ alpha * (global_best_pos[j] - manta[i].position_[j]);
}
}
}
if (manta[i].value < global_best_value){
gbest_num = i;
global_best_value = manta[gbest_num].value;
for(int j=0; j<dimension_; j++){
global_best_pos[j] = manta[gbest_num].position_[j];
// printf("gbp %d: %f\n",j, global_best_pos[j]);
}
}
}
// Somersault Foraging
for (int i=0; i<population_n; i++){
r2 = ((double)rand() / RAND_MAX);
r3 = ((double)rand() / RAND_MAX);
for (int j=0; j<dimension_; j++){
manta[i].position_[j] = manta[i].position_[j]
+ s * (r2 * global_best_pos[j] - r3 * manta[i].position_[j]);
}
}
printf("global best: (x, y) = %f, %f: value = %f\n",
global_best_pos[0], global_best_pos[1], global_best_value);
}
int main(){
srand((unsigned int)time(NULL));
Mrfo foraging;
for (int i=1; i<5; i++){
printf("Generation %d, ", i);
foraging.move(i, 5);
}
return 0;
}
上記では、Mrfoという一つのクラスに実装で必要なものはすべて入れ込んであります。
マンタ単体は構造体 struct manta_ray内で定義されており、マンタの個体ごとに位置:position、評価値:valueを持っています。
それをstruct manta_ray *mantaでポインタの構造体として、群れを作るようプログラムしています。
MRFOでは餌であるプランクトンの割合:populationに応じて、マンタが連鎖(Chain)したりサイクロン採餌をするので、population≒マンタの数と捉えて良いと思っています。
PSO同様、コンストラクタで各マンタの初期位置、グローバルベスト等を求めたら、実施に採餌行動のプログラムを書くのみとなります。
採餌行動のプログラムは全てMrfo::move(int current_iter, int max_iter)で記述されています。
まず各マンタは、乱数によりCyclone ForagingかChain Foragingのどちらで採餌するかを選びます。
乱数が0.5より小さいときはCyclone Foragingで採餌を開始し、全体に対する現在の反復回数を示すcoefが乱数より小さい場合はxrandを用いてランダム探索を、乱数より大きい場合はグローバルベストを用いた探索を行います。
乱数が0.5以上のときはChain Foragingにより採餌します。
Cyclone,Chain Foragingのどちらかが終了したら、一度グローバルベストを更新し、Somersulat Foragingを行います。
これにより最終的な局所最適解を求めます。
以上3つの採餌行動を指定した最大反復回数max_iter分繰り返すことで、より正確な最適解を求めることができます。
ROS2/C++でMRFOを実装する
ROS2/C++でMRFOを実装するに当たり、以下のように調整していきます。
入力データ(Float32 /input)を受け取ると、MRFOにより局所最適解を求めるようなプログラムとし、餌の割合≒マンタの数(population)、解候補の次元(dimension)、最大反復回数(max_iter)をparameterで変更できるようにしています。
また、最終的に算出した局所最適解は出力データ(Float32 /output)としてpublishできるようにしています。
MRFOのROS2/C++実装例
各関数はC++実装のときと変わらないので、とりあえず全文載せていきます。
各パスの関係は、お手数をおかけしますがご自身の環境・スタイル似合わせて変更してください。
#ifndef SWARM_INTELLIGENCE_ROS2__MRFO__MRFO_COMPONENT_HPP_
#define SWARM_INTELLIGENCE_ROS2__MRFO__MRFO_COMPONENT_HPP_
#include <stdlib.h>
#include<stdio.h>
#include <time.h>
#include <cfloat>
#include <cmath>
#include "rclcpp/rclcpp.hpp"
#include "std_msgs/msg/float32.hpp"
class MrfoComponent : public rclcpp::Node
{
public:
MrfoComponent(const rclcpp::NodeOptions & options);
~MrfoComponent();
void move(int current_iter, int max_iter);
struct manta_ray{
double *position_ = nullptr;
double value;
};
struct manta_ray *manta; //Declarations that use pointers in structures
double *global_best_pos = nullptr;
double global_best_value = DBL_MIN;
int gbest_num;
private:
rclcpp::TimerBase::SharedPtr timer_;
rclcpp::Publisher<std_msgs::msg::Float32>::SharedPtr publisher_;
rclcpp::Subscription<std_msgs::msg::Float32>::SharedPtr subscriber_;
void timer_callback(const std_msgs::msg::Float32::SharedPtr msg_data);
void manta_init();
void evaluate(int population);
int dimension_; // MantaRays dimensions = number of solutions
int population_n; // the size of plankton population 餌の数
int max_iter; // maximum number of iterations 反復回数
double xminj = -1;
double xmaxj = 1;
double rand_select_foraging;
double coef;
double cutoff_rand, r, r1, r2, r3, xrand;
double alpha, beta;
const int s = 2; // somersault factor that decides the somersault range of matna rays
};
#endif // SWARM_INTELLIGENCE_ROS2__MRFO__MRFO_COMPONENT_HPP_
#include "swarm_intelligence_ros2/mrfo/mrfo_component.hpp"
using namespace std::chrono_literals;
MrfoComponent::MrfoComponent(const rclcpp::NodeOptions & options)
: Node("mrfo_node", options)
{
this->declare_parameter("dimension", 2);
this->declare_parameter("population", 30);
this->declare_parameter("max_iter", 5);
subscriber_ = this->create_subscription<std_msgs::msg::Float32>(
"/input",
10,
std::bind(&MrfoComponent::timer_callback, this, std::placeholders::_1)\
);
publisher_ =
this->create_publisher<std_msgs::msg::Float32>("/output", 10);
}
MrfoComponent::~MrfoComponent()
{
delete [] manta->position_;
delete [] global_best_pos;
}
void MrfoComponent::timer_callback(
const std_msgs::msg::Float32::SharedPtr msg_data)
{
srand((unsigned int)time(NULL));
// Get parameter
dimension_ = this->get_parameter("dimension").get_parameter_value().get<int>();
population_n = this->get_parameter("population").get_parameter_value().get<int>();
max_iter = this->get_parameter("max_iter").get_parameter_value().get<int>();
// Initialize manta
this->manta_init();
double input_data = msg_data->data;
RCLCPP_INFO(this->get_logger(), "subscribe data %f:", input_data);
std_msgs::msg::Float32 data;
std_msgs::msg::Float32 data2;
// request->a = number of iterations
for (int i=0; i < max_iter; i++){
RCLCPP_INFO(this->get_logger(), "Generation %d:", i);
this->move(i, max_iter);
}
data.data = global_best_pos[0];
data2.data = global_best_pos[1];
publisher_->publish(data);
publisher_->publish(data2);
RCLCPP_INFO(rclcpp::get_logger("rclcpp"), "global best (x, y): (%f, %f)", data.data, data2.data);
}
void MrfoComponent::manta_init(){
// Initialize the manta ray
manta = new manta_ray[population_n];
for (int i=0; i<population_n; i++){
manta[i].position_ = new double[dimension_];
for (int j=0; j<dimension_; j++){
manta[i].position_[j] = xminj + (xmaxj - xminj) * ((double)rand() / RAND_MAX);
}
this->evaluate(i);
}
// Initialize global best pos and value
global_best_pos = new double[dimension_];
gbest_num = 0;
for (int i=0; i<population_n; i++){
if(manta[i].value < manta[gbest_num].value){
gbest_num = i;
}
}
global_best_value = manta[gbest_num].value;
for (int j=0; j<dimension_; j++){
global_best_pos[j] = manta[gbest_num].position_[j];
}
}
void MrfoComponent::evaluate(int population){
double A = manta[population].position_[0];
double B = manta[population].position_[1];
manta[population].value = A*A + B*B;
}
void MrfoComponent::move(int current_iter, int max_iter)
{
for (int i=0; i < population_n; i++){
// Cyclone Foraging
rand_select_foraging = ((double)rand() / RAND_MAX);
if (rand_select_foraging < 0.5){
// RCLCPP_INFO(this->get_logger(), "Cyclone:");
coef = double(current_iter)/double(max_iter);
cutoff_rand = ((double)rand() / RAND_MAX);
r = ((double)rand() / RAND_MAX);
r1 = ((double)rand() / RAND_MAX);
beta = 2 * std::exp(r1*(max_iter - current_iter + 1) / max_iter) * sin(2 * M_PI * r1);
if (coef < cutoff_rand){
// RCLCPP_INFO(this->get_logger(), "cutoff\n");
xrand = xminj + (xmaxj - xminj) * ((double)rand() / RAND_MAX);
for (int j=0; j<dimension_; j++){
if(i == 0){
manta[i].position_[j] = xrand
+ r * (xrand - manta[i].position_[j])
+ beta * (xrand - manta[i].position_[j]);
}
else{ // population = 2 - N
manta[i].position_[j] = xrand
+ r * (manta[i-1].position_[j] - manta[i].position_[j])
+ beta * (xrand - manta[i].position_[j]);
}
}
}
else{
// RCLCPP_INFO(this->get_logger(), "normal\n");
for (int j=0; j<dimension_; j++){
if(i == 0){
manta[i].position_[j] = global_best_pos[j]
+ r * (global_best_pos[j] - manta[i].position_[j])
+ beta * (global_best_pos[j] - manta[i].position_[j]);
}
else{ // population = 2 - N
manta[i].position_[j] = global_best_pos[j]
+ r * (manta[i-1].position_[j] - manta[i].position_[j])
+ beta * (global_best_pos[j] - manta[i].position_[j]);
}
}
}
}
// Chain Foraging
else{
// RCLCPP_INFO(this->get_logger(), "Chain\n");
r = ((double)rand() / RAND_MAX);
alpha = 2 * r * (sqrt(fabs(log(r))));
for (int j=0; j<dimension_; j++){
if(i == 0){
manta[i].position_[j] = manta[i].position_[j]
+ r * (global_best_pos[j] - manta[i].position_[j])
+ alpha * (global_best_pos[j] - manta[i].position_[j]);
}
else{ // population = 2 - N
manta[i].position_[j] = manta[i].position_[j]
+ r * (manta[i-1].position_[j] - manta[i].position_[j])
+ alpha * (global_best_pos[j] - manta[i].position_[j]);
}
}
}
if (manta[i].value < global_best_value){
gbest_num = i;
global_best_value = manta[gbest_num].value;
for(int j=0; j<dimension_; j++){
global_best_pos[j] = manta[gbest_num].position_[j];
}
}
}
// Somersault Foraging
for (int i=0; i<population_n; i++){
r2 = ((double)rand() / RAND_MAX);
r3 = ((double)rand() / RAND_MAX);
for (int j=0; j<dimension_; j++){
manta[i].position_[j] = manta[i].position_[j]
+ s * (r2 * global_best_pos[j] - r3 * manta[i].position_[j]);
}
}
RCLCPP_INFO(this->get_logger(), "global best: (x, y) = %f, %f: value = %f\n",
global_best_pos[0], global_best_pos[1], global_best_value);
}
#include "rclcpp/rclcpp.hpp"
#include "swarm_intelligence_ros2/mrfo/mrfo_component.hpp"
int main(int argc, char * argv[])
{
rclcpp::init(argc, argv);
rclcpp::NodeOptions options;
auto component = std::make_shared<MrfoComponent>(options);
rclcpp::spin(component);
rclcpp::shutdown();
return 0;
}
あとは下記のように、入力データとして適当にFloat32のデータ/inputをsubsclibeして、outputでMRFOの局所最適解を/outputとしてpublishできていればOKになります。
以上、どなたかのお力添えになれば幸いです。
LikeやGithubのスター頂けると大変励みになるので、よろしくお願いいたします。
本記事のプログラム
本記事で扱ったプログラムは、下記のGithubからもご覧いただけます。
References
・Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications
・Github: angelinbeni/Manta-Ray-Foraging-Optimization
・Github: Rohit-Kundu/Hybrid_MRFO-OBHSA
・Youtube: Learn Manta Ray Foraging Optimization (MRFO) Algorithm Step-by-Step Explanation ~xRay Pixy


Discussion