2進数332億桁→10進数100億桁を効率よく求めるはなし
またまた (まだまだ) 円周率100億桁かよ。
10進数100億桁→2進数332億桁の変換は、なんとかやってみた。つか、そもそも考えてみたらgmpy2は2進数で計算してるので、10進で表示したのを2進に戻すのもおかしなはなしで。
こんかいは、2進数で計算しているのを10進で表示しよう……とそれ、Python (gmpy2) のprint() (バイナリ→文字列) 変換じゃん? と思われるかもしれないが……そう、そこって100億桁程度の固定小数点で多桁演算していると、速度のボトルネックになっているのだった。10コアあるMacbook Proでも64コアのAWSを借りても、1コアで延々割り算を続けている。
そこを並列化したい、というはなしである。
そもそもわしは何やってんだろ? (お題の制約)
円周率 (その他の数) を多桁求めるガチ勢は、y-cruncherとかそれ用のプログラムを使っている。自分でPython (gmpy2) の整数演算でプログラム書いてるやつは、たぶんいない(笑)。シングルCPUなのでVM (メモリ) 制限には引っかかるし (いや実は自分で通信書けば、複数CPU並列もできるんだけど)、特にそういう込み入ったマシン間通信を構成したり並列CPU演算を書いたりしなくても (※ 並列プロセスは書いてるけども) 割とお手軽に、世界人口くらいの桁数の多倍長演算ができますよ、って楽しみです。車があるのに脚で走って100m10秒を切る記録、みたいな、縛りの下でのお遊び、っていいますか。まあ、y-cruncherガチ勢にしても、「ただ他人のプログラム使ってるだけじゃん」みたいな悪口もきかれるが、多数の機器を長時間動かす構成をして、HDD・メモリのエラーと戦いながら数ヶ月、って、並の苦労ではありません。そんな苦労をして作ってるのが円周率とか変態な数なのだから、わしと同じく「何やってんだろ」感はあると思うんだけどね(笑)。
はてさて、そうすると冒頭で書いたように、Python (gmpy2) の2進バイナリ (馬から落馬) を10進文字列に変換する部分も、Pythonの中でという縛りが必要である。バイナリをpickleファイルとかバイナリ列にして、Cでマルチプロセス文字列変換プログラムを書いたり、っていうのは、なしの方向にしたい。
となると、gmpy2の2進→10進変換する部分 (low level関数のmpn_set_str()らしい) がなにをしているのかが気になる。いろいろ探すと、2017年からは
なるアルゴリズムが使われているようである。
つまり、このままでもそこそこ速い。いや、この関数を自分でCで書いて置き換えたところで、これ以上速くならないかもしれない。
となると、速くする余地があるのは並列化の部分である。つまり、2進数列をてきとーに分割して→マルチプロセスに振って10進に変換→結合すると長い10進文字列がどん、というように、なんとかできないものか。
閑話: 5進数の呪い〜2進小数点以下の10進変換
ちょっと、2進小数部の任意の桁から2進→10進変換する方法を考えてみた。
通常、小数点以下の基数変換というのは上の方の桁から重みを掛けて足す。例えば2進数の小数点以下3ビット目を10進数で表わした重み『0.125』の3桁目『5』 (ややこし) は、上の方の桁『12』抜きには語れない。
さて、わしが円周率を求めている方法では固定小数点、つまり小数点以下の数は何倍か (
円周率を求める場合をはじめ、BBP法で変態な級数を求めるとき、小数点以下の演算、(整数 ÷ 整数) は最後の1ステップのみに出てくる。結果も固定小数点にしたいので、例えば10進100億桁の場合は分子に
もし最後の答を2進小数部として表現するなら、小数点以下求めたいビット数を
これを考え始めたら、2進 (固定小数点表現) 小数部の10進変換は、5進数の10進変換であることがわかった。
2進数の小数点以下は、重みが
1
0.5
0.25
0.125
0.0625
0.03125
0.015625
0.0078125
0.00390625
0.001953125
0.0009765625
0.00048828125
0.000244140625
0.0001220703125
0.00006103515625
0.000030517578125
0.0000152587890625
0.00000762939453125
0.000003814697265625
0.0000019073486328125
...
と、美しい三角形になる。
出てくる数字を眺めてみると、0をサプレスした数字は5進数の整数部の重み (
結論から言うと、これを眺めていたら、並列処理で2進小数→10進小数を得るのは難しそうだ……と感じた。
桁の重み
並列処理で知りたいのは、2進
成り立ちから考えて、各桁は
1
\
5
|\
2 (5)
|
(1)
というパズルのピースの重ね合わせで出来ている。((1)のところには次のピースの1を、(5)のところには5をはめて、各桁を足していく)。だがこれも、2進数
数字列の法則に着目してみる。
(上の方を除いて) 下2桁は『25』であるのは簡単にわかるが、面白いことに下3桁は『125』『625』が繰り返している。というか、下から3桁目は『16』 (1つ離れると5大きくなる) の繰り返しである。下から4桁目は同様に『0358』 (2つ離れると5大きくなる) の繰り返し、5桁目は『01795624』 (4つ離れると5大きくなる) の繰り返しである。なにやら循環小数 (割る数の
では数列の最初の数はどうやって求めるかといえば、これは最初にその数が出てくる (例えば3桁目は
ということで、
積算される10進レジスタの幅 (必要桁数)
結果、つまり重みが積算される10進レジスタの長さだが、できれば確定した上位桁はちゃっちゃと出力するなりして、捨ててしまいたい。ところが、見ての通り三角形の右側はきっちり、2進小数以下
もちろん、
つまり、10進
閑話休題: 2進整数 (固定小数点) の10進変換
ということで2進固定小数点表現→10進数への変換は諦めて、ふつーに10進のべき乗を掛けて除算した、10進整数の2進変換のはなしに戻る。
この場合は、もともとの実数計算 (BPP法なら、最後の除算1回だけ) で『実数が'0.'』とか付けるだけでよい。
2進整数部なら倍、倍で増えていくだけなので、
そもそもこの記事の趣旨は、まとまった桁数のそこそこ速い (だが並列化されていない) 2→10進変換 (gmpy2の) を利用して、100億桁を1コアでいっぺんに変換するのではなく、部分的な数億桁を並列に変換してやろう、ということである。
10進数で
さて
アルゴリズム1. ちぎっては投げ
- 10進数の桁数
N p -
M = N / p n_1, r_1 = n 10^M -
r_1 d_1 -
n_2, r_2 r_1 10^M - 以下
(p - 1) - 最後に残った (おおむね
M n_p d_p
-
- 各子プロセスから集めた、10進変換済み (
M d_p, \ldots, d_1
結果が合わなくてハマったはなし
最初何も考えずに子プロセスからの戻り (文字列) を結合したら、なんか結果がおかしい。
100桁くらいの少ない桁数で、シングルプロセス (つまりふつーに2進→10進変換) した結果とマルチプロセス化した結果を比べたら……たまたま分割した切れ目の上位が『0』 (またはその連続) だと、桁が足りなくなってしまう。当たり前ですけど。『
下のプログラムでは、fpartprint()のnpadの個数だけ'0'を追加して、本来の桁数だけ右から切って返してます。無理数系ではこれでいいんだけど (つまり10分割した9個の切れ目に0がnpad個連続する確率は、
いちおう、いろいろな桁数でシングルプロセス版で吐いたテキストファイルと、このアルゴリズムが吐いたのとのmd5が一致することは、都度確認している。
これなら、たとえば10プロセスに分けるため100億桁を10にちぎれば、最大でも (100億桁 ÷ 10億桁) の除算なので、これは可能である。
アルゴリズム1.を思いついて実装し、色々調べていると、半分にちぎって再帰する (同じように複数のプロセスに分けてもよい) という方法が既知らしい。こんかいの円周率 (その他) は100億桁がお題なので、最大 (100億桁 ÷ 50億桁) の除算が出てくるが、VMは不足しないだろうか。最初に『半分に分ける』ところさえクリアできればよい。
アルゴリズム2. 半分にして再帰
- 10進数の桁数の半分くらい (
0.15N M n 10 ^M n_1, n_2 - あと
n_1, n_2 n_2 M - 再帰すれば、いくらでも計算量は減らせるだろう(?)
- あと
- できた値をつなぐ
問題は、Pythonの2進 (intまたはgmpy2内部表現)→10進 (文字列) 変換が、そこそこ速いことである (ってかgmpy2の場合はたぶん、高速な基数変換アルゴリズムがCとかで実装されている)。シングルプロセスで100億桁の2進→10進変換をするのが速いか、10個のプロセスに分けるが (100億桁 ÷ 10億桁) 〜 (20億桁 ÷ 10億桁) の除算 (これは親がシングルプロセスで行なう) をしながらの方が速いか。
『ちぎっては投げ』の実装
こんなプログラムを作って、試してみた。
プログラム1. gmpy2 多桁2進→10進変換 ちぎっては投げ (プログラムリスト)
import math
import gmpy2
from gmpy2 import mpz
from concurrent.futures import ProcessPoolExecutor as Executor
import time
import sys
def strpart(n):
return str(n)
def fpartprint(n, ndiv, rate, fn):
npad = 10 # 分割した頭が0の場合は、npad桁の'0'を追加して桁数に切る
if rate != 1.:
rsum = (rate ** ndiv - 1.) / (rate - 1.)
else:
rsum = ndiv
print('rate', rate, 'rsum', rsum)
#tdig = int(math.ceil(gmpy2.num_digits(n) / ndiv))
# ↑これだとleading zeroがあるときうまくいかない
tdig = int(gmpy2.num_digits(n) / rsum)
future = [0] * ndiv
dig = [0] * ndiv
top = n
with Executor() as exec:
for i in range(ndiv - 1, 0, -1):
base = mpz(10) ** tdig
top, bot = gmpy2.f_divmod(top, base)
future[i] = exec.submit(strpart, bot)
dig[i] = tdig
print('exec {} ({}) - '.format(i, tdig), end = '', file = sys.stderr)
tdig = int(tdig * rate)
print('exec', 0, file = sys.stderr)
sr = strpart(top)
print('done', 0, end = '', file = sys.stderr)
with open(fn, 'w') as fp:
print(sr, end = '', file = fp)
for i in range(1, ndiv):
s = ('0' * npad + future[i].result())[-dig[i]:]
print('done', i, end = '', file = sys.stderr)
print(s, end = '', file = fp)
print('', file = fp)
print('', file = sys.stderr)
多桁2進→10進変換 テスト用メイン (プログラムリスト)
if __name__ == '__main__':
# ndiv: プロセス分割数は決め打ち、桁数digは引数から
ndiv = 20
if len(sys.argv) != 2:
sys.exit(1)
dig = int(sys.argv[1])
print('making', dig, 'digtits test data...', end ='', file = sys.stderr)
t = mpz(2) * (mpz(10) ** (dig * 2))
t = gmpy2.isqrt(t)
print('done', file = sys.stderr)
# シングルプロセス: gmpy2 2進→10進変換 (時間がかかるのでコメントアウト)
# stt = time.time()
# s = str(t)
# et1 = time.time() - stt
# with open('test1.txt', 'w') as fp:
# print(s, file = fp)
# print(et1, file = sys.stderr)
# マルチプロセス: rate = .6〜1.
for rate in [.6, .7, .8, .9, 1.]:
stt = time.time()
fpartprint(t, ndiv, rate, 'test2.txt')
et2 = time.time() - stt
print(et2, file = sys.stderr)
メインでは、テスト用に
プログラム中ndivが分割プロセス数 (親含む)、rateが後述の子供ごとに桁数に差をつけるレート (等比数列) です。ここまでのはなしの『桁数を10プロセス均等割』はrate = 1.、ndiv = 10の場合。
結果はこの通り。

紫: シングルプロセス(gmpy2の2→10進変換)、緑: 5プロセス、青: 10プロセス、橙: 20プロセスに分割
はじめ、シングルプロセスの (つまり元々の) 2→10進変換と、10コアなのだから10プロセスに分けたものとを比較していたが、これでは1億桁まではマルチプロセスのほうが遅くなる。それ以上でやっと逆転し、10億桁でやっと3割速くなる程度である。
観察しているとやはり、子プロセスにちぎっては分けるところ (10のべき乗での除算) で時間がかかっており、下手すると最初の子は最後の子と親が変換を初めたころには仕事を終えている、のが原因らしい。
では、ちぎる桁数を増やす、つまりプロセス数を減らすとどうか。
3〜20コアくらいまで変えていろいろな桁数で試してみるとなんと、4コア〜5コアが最適で、1億桁なら4コアで、10億桁では5コアで4割弱速くなっている。
これも根本的には『早く着手した子が先に終わる』問題は残る。そうか、では最初の子にはたくさんの桁を渡し、最後の子と親は変換桁数を減らすようにしたらどうか。桁数の小っちゃくなり方は等差なのか等比なのかそれとももっと複雑なカーブが良いのか……どうも、『ちぎる』操作で必要なgmpy2のf_moddiv() (商と余りを求める) と、2進→10進変換は、
最初と同じプロセス数5の場合はこのとおり。
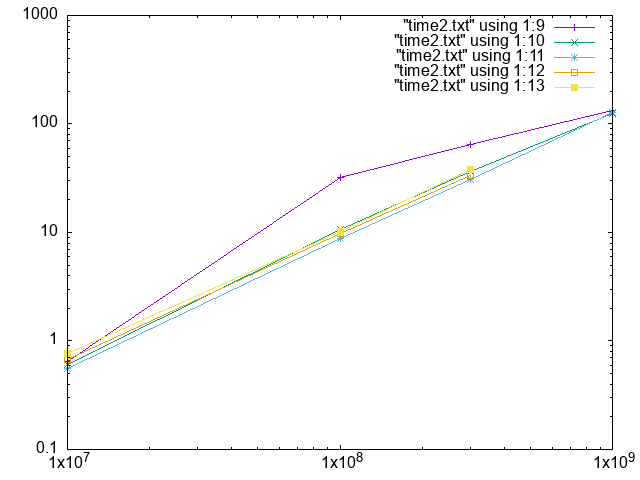
(すべて5分割) 紫: レート0.6、緑: 0.7、青: 0.8、橙: 0.9、黄: 1. (均等割)
対数だと差が微妙すぎてわからんが (実感では2分中の10秒とかなので結構、速くなると喜ぶ)、0.6では明らかに最初の分割で桁数が大きいので時間がかかり過ぎ、最初の子に仕事が行き過ぎる。桁数が多くなると0.7の優勝が確定するようだ。
こんどは最大効率くらいまで使えるのではないかと踏んで、コア数10と同じプロセス数10の場合はこのとおり。

(すべて5分割) 紫: レート0.6、緑: 0.7、青: 0.8、橙: 0.9、黄: 1. (均等割)、紺: 5分割のレート0.7
10コアの場合でも1000万〜10億桁くらいまでは5コアの場合と大差ない。最大効率で動くということはなくて、親が桁をちぎっている間は子供が待っているわけで、理想的に同時に終わったとしても等比数列の和から10コアで25% (レート0.6の場合)〜65% (0.9の場合)、5コアで23% (0.6)〜40% (0.9) しか2進→10進変換に使われない。
100億桁の変換ならば10コアに分けたのは効果絶大、10コアでレート0.6〜0.9まで一晩かけて試してみました。シングルコアでは50分掛かるところ、25分くらいで済んでいる!!
『2分割して再帰』の実装
すでにアルゴリズム1.を実装して計算時間半分くらいにはなっているのだが、アルゴリズム2. (既知)の 『2分割して再帰』は果たしてそれより効率が良いだろうか?
VMに関しては、(200億桁 ÷ 100億桁) はできなかったけど、こちらは最大で (100億桁 ÷ 50億桁) の除算である。ただし、アルゴリズム1. の(100億桁 ÷ 10億桁) よりは(100億桁 ÷ 50億桁)のほうが時間がかかる。が、その後は半分半分 (50億桁 ÷ 25億桁)、(25億桁 ÷ 12.5億桁)、……になっていくので、(90億桁 ÷ 10億桁)、(80億桁 ÷ 10億桁)、……と減っていくのと、どちらが効率が良いだろうか?
プログラム2. gmpy2 多桁2進→10進変換 2分割して再帰 (プログラムリスト)
import math
import gmpy2
from gmpy2 import mpz
from concurrent.futures import ProcessPoolExecutor as PExecutor
import time
import sys
maxproclev = 5
def decconv(n, dig, lev):
npad = 20
if maxproclev < lev:
return ('0' * npad + str(n))[-dig:]
topdig = dig // 2
botdig = dig - topdig
base = mpz(10) ** botdig
top, bot = gmpy2.f_divmod(n, base)
del n, base
with PExecutor() as exec:
future2 = exec.submit(decconv, bot, botdig, lev + 1)
del bot
s = decconv(top, topdig, lev + 1)
del top
s += future2.result()
return ('0' * npad + s)[-dig:]
プログラム2. 多桁2進→10進変換 テスト用メイン (主要部分のみ) (プログラムリスト)
stt = time.time()
s = decconv(t, dig + 1, 0)
et2 = time.time() - stt
print(et2, file = sys.stderr)
with open('test2.txt', 'w') as fp:
print(s, file = fp)
例によってグラフは微妙で見づらいが、全コアを駆使しようと16プロセス (maxproclev = 3) まで増やしてみたところ、まだまだプロセスに分けると速くなる。64プロセス (maxproclev = 5) では速くなったが、128プロセス (maxproclev = 6) ではさすがに遅くなってきた。

紫: プロセス分割数16、緑: プロセス分割数32、青: プロセス分割数64、橙: プロセス分割数128、黄: ちぎっては投げ法(レート0.7)、紺: gmpy2の2進→10進変換
結局100億桁でテストしてみると、64プロセスに分割した方法では『ちぎっては投げ』レート0.7の場合とほぼ同じ結果が得られた (実時間で1513秒と1593秒だが、実時間は他の影響もあるので誤差の範囲だろう)。
『再帰2分割法』を『ちぎっては投げ』法と比較すると
- 上のグラフでは、オリジナル (1コアでの2進→10進変換) からの差異がわかるようにして満足感に浸っているが(笑)、確かに2倍速くなったら差は大きいものの、平行だ (つまり計算量オーダは減らない)
- なぜか最適な点ではどちらも同じくらいの速度 (それもオリジナルのちょうど2倍) に落ち着いている。なにか『マルチコアにしてもこれ以上速くならない』理論的な限界がここにあるのかもしれない、と思ったり。知らんけど
- 短くした2進数列の10進変換はどのプロセスも等しく受け持っている。スタートも同じ (はず) なので、どの子供にどのくらいの仕事をもたせるか (『レート』) のチューニングは必要ない。……が、やはりCPUコア数で分割 (再帰レベル) は選ばないといけないようだし、再帰レベルは
2^n - メモリは余計に喰う
ハマったポイント
さいしょは何も考えずにプログラム1. を単純に変更して、落ちた(笑)。使わない変数をまめにdel、他のブラウザとかを終了してなんとか……最大メモリ使用量35GBくらい? (マルチプロセスなので目の子で合計したが) で100億桁の実行を終えることができた。
maxproclevは再帰 (プロセスを起動する) 段数なので、maxproclev = 5ではレベル0〜5まで
ふと思いついてマルチプロセスではなくマルチスレッドに分けてみても (同じconcurrentパッケージで1行変更するだけでOK)、もちろんCPU使用率は上がらない。あるレベルまではプロセス分割、それ以上に少しスレッドに分けてみてもそれほど効率は上がらない。結局、マルチプロセス (勝手にスレッド分けされてる?) で、プロセス数は128までできないものの最速が出るところを実験的に突き止めた。
まとめ
長々書いてきたが、既にもう100億桁は
しかも今回うんうん唸って2倍速くしたところで50→25分だし、円周率その他込み入った計算では本体の演算に時間が掛かるが、
とはいえ、桁数が大きい場合に高速といわれるgmpy2の2進→10進変換がプロセス分割することでまだ2倍速くする余地がある (プロセス分割のオーバヘッドでせいぜい2倍にしかならない?)、という知見は得られた。ことにする、知らんけど(笑)。
今回は、ほんとうに自己満足でした〜。


Discussion