1.概要
2021/04/29 に行われた「第 1 回競技プログラミングリーグ戦」で「オイラー法」を使う問題が出題されました。オイラー法の定義は問題文に記載されていたのですが、感覚的にどういったことをしたいのか理解できた方は少ないと思います。
本記事では、オイラー法の感覚的理解を目標として、オイラー法の説明をしていきいます。
2.関数とは何か
オイラー法の説明に行く前に、まずは「関数とは何か」を抑えておきましょう。理解ができている方は読み飛ばしてください。ちなみに本記事における関数とは、特に指定がない限りは「数学における関数」のことを指します。
言葉の定義
関数とは、簡単に言えば「関わる数」「関りがある数」「関係のある数」という意味です。読んで字のごとく、ですね。しかし、「関係のある」という言葉は通常二つ以上のものに対して使うものですので、これだとちょっと意味が把握しづらいかもしれません。具体例を見てみましょう。
よく「 y は x の関数である」という文句を見聞きしませんか?これは、「 y の値は x の値に関りのある数ですよ」という内容を端的に表現した文句です。もう少し踏み込んで言うと「 x の値が一つに定まった時、 y の値はただ一つに定まる」ということを表しています。
関数のグラフ
みなさんは、下のような図を見たことがありませんか?
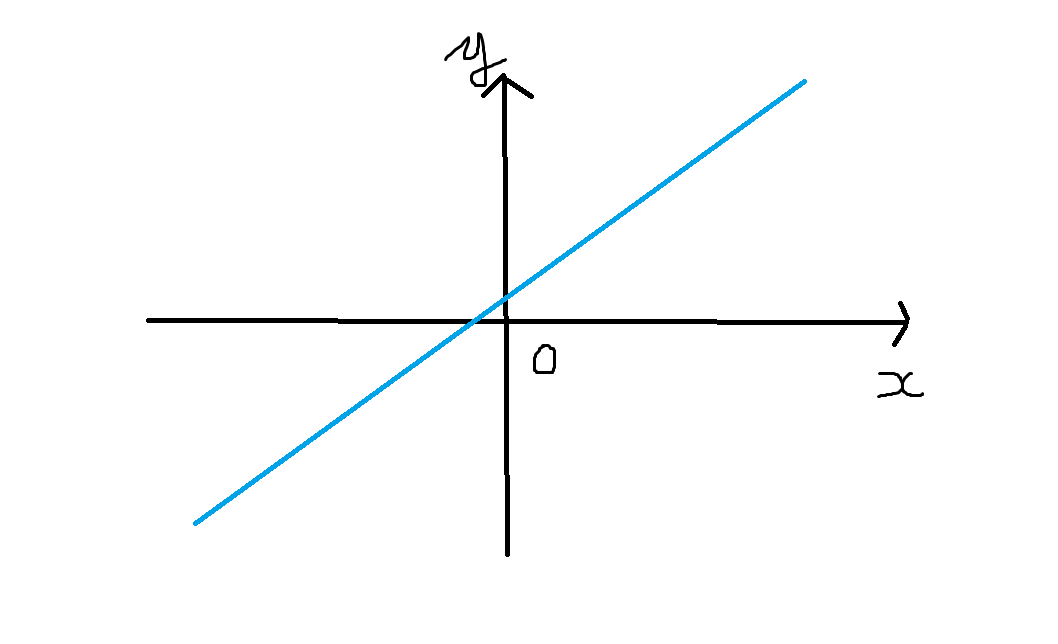
水色の線は、 x の値とそれに対応する y の値が示す点の集合です。このように、互いに関係のある二つ以上の数量を図に描いたものをグラフと呼びます。
グラフは視覚的に関数の特徴を理解するのに便利ですので、今後の説明でも多用していきます。
では、突然ですが一つ問題です。下に四つのグラフがあります。このうち、「 x が y の関数」であるときのグラフを全て答えてください。
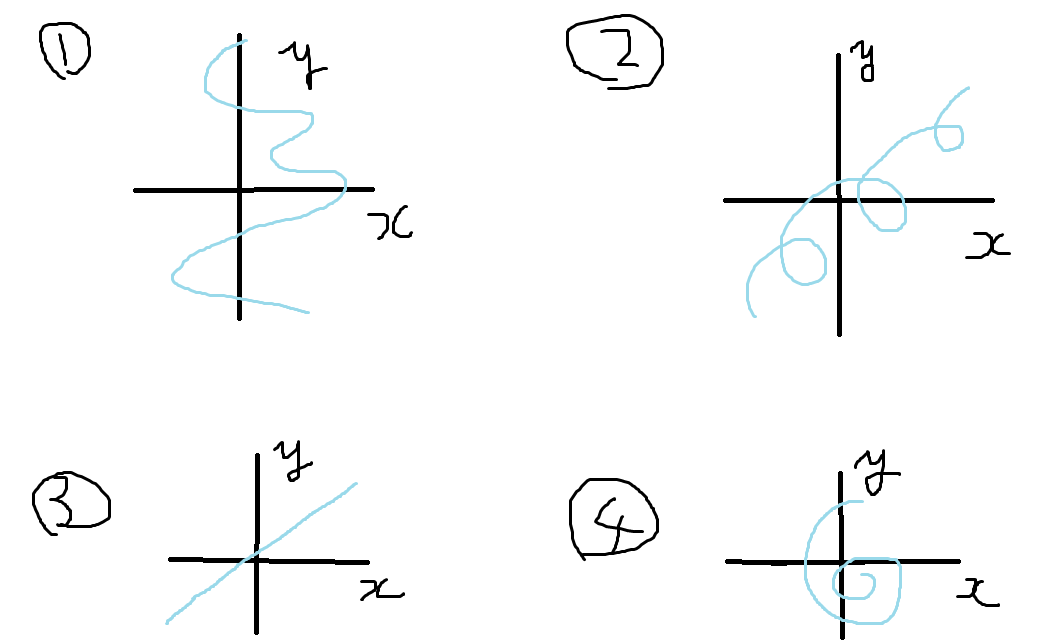
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・正解は①と③です。
「 x が y の関数である」とは、「 y の値が一つに定まった時、 x の値はただ一つに定まる」ということです。この定義に則って考えると、正解は①と③になります。
関数の理解はこれくらいで大丈夫でしょうか?今回は x と y の二つの文字しか出てきませんが、もっとたくさんの文字が出てくるような関数もあるので、興味のある方はぜひ調べてみてください。
3.微分
オイラー法を理解するには、微分の理解が必須です。しかし、微分を理解するためには極限の理解が必要になり、 0 からすべてを理解するには時間が必要です。しかし、感覚的な理解であればそこまで難しくはありません。
平均変化率という考え方
下のグラフを見てください。
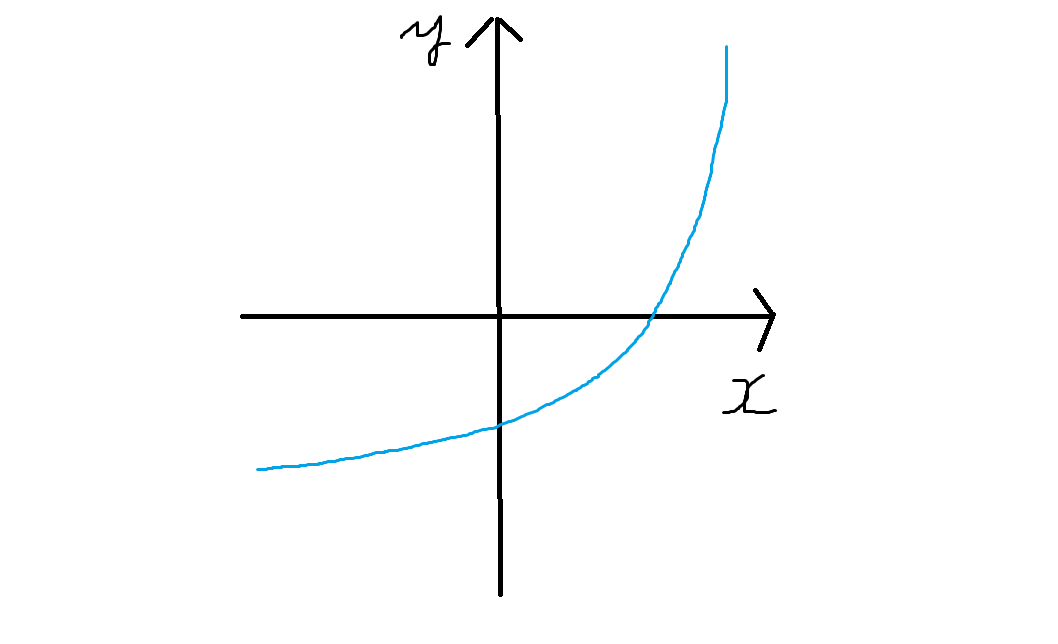
x の値が小さいほうから大きいほうにかけて、 y の値がグーッっと上昇していますね。ここで、 x の値が a から b にかけて変化するとき、「平均して」 y の値がどう変化しているのかをグラフで表してみたいと思います。
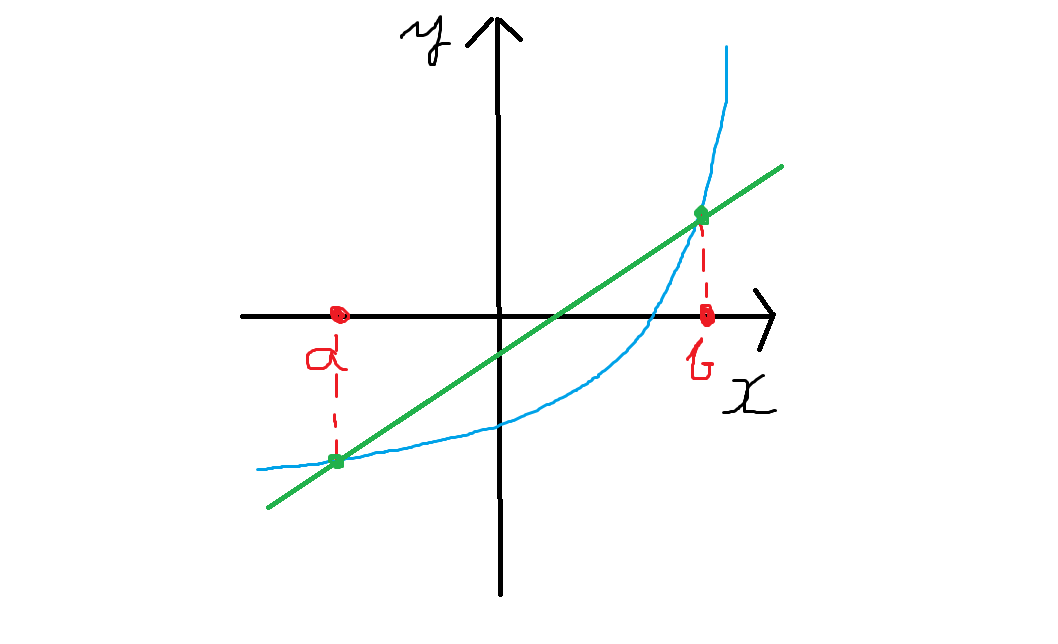
緑の直線が、変化を平均的に表したものです。実際には、水色の線には緩く上昇してる部分と急激に上昇している部分がありますが、均すとこのような直線としてあらわされます。また、この緑の直線の傾きを、「 x が a から b まで変化するときの平均変化率」と言います。
ある一点における平均変化率
先ほど、「 x が a から b まで変化するときの平均変化率」を求めました。では、この a と b の間を限りなく狭めていくことを考えてみましょう。数学的には「 b−a を 0 に(限りなく)近づける」というような言い方をします。
(この「限りなく近づけるという操作」のことを「極限」あるいは「極限を取る」と言います。極限は、「値を限りなく近づけるだけであって、決してイコールにはならない」ということが一つ大事なポイントになるのですが、本記事でそれを厳密に説明するのは大変なので、極限の説明はここまでにしておきます。気になる方は自分で調べるか、学校の先生に聞いてみてください。)
b を a に近づけていった時のグラフは、下のようになります(汚くてすみません…)。
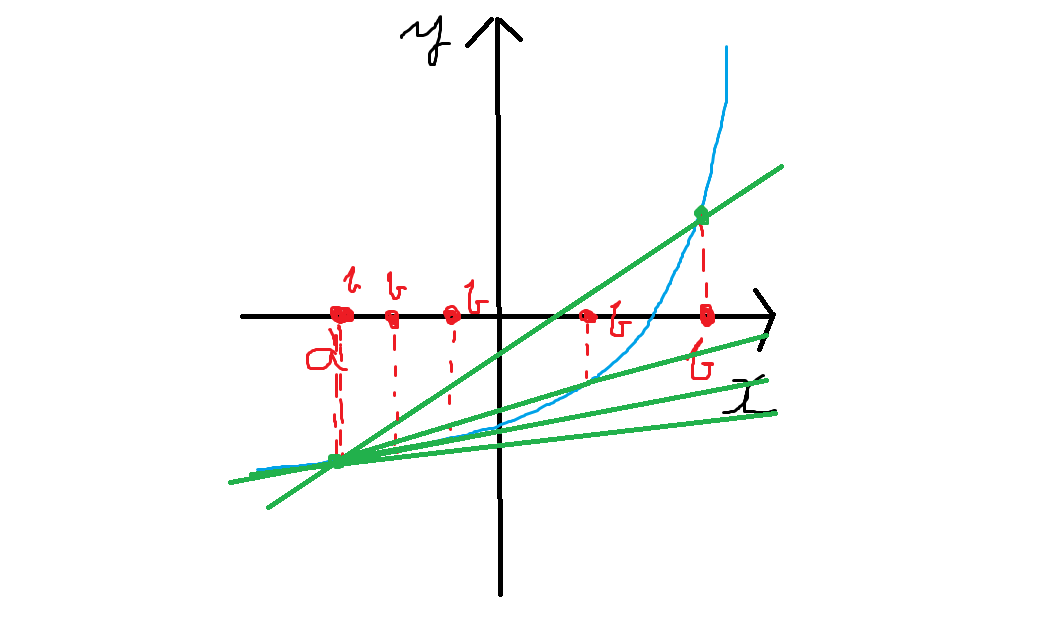
このように、 b を限りなく a に近づけていくと、最終的には x=a におけるグラフの傾きを求めることができます(ほんとかよ、と思う方は極限を勉強してください)。
今したことを整理すると、 x の値の差分を限りなく小さくしていった時の、 y の平均変化率を求めました。実はこの操作が「微分」なのです。「 x の値の差分を限りなく小さくしていった時の、 y の平均変化率」は「ある点におけるグラフの傾き」に等しいので、「微分とはグラフの傾きを求める操作である」と説明されることも多いです。
感覚的には、微分がどういうものなのか理解できたでしょうか?じゃあ数式でどうやって表すんだ、ということはここでは扱いませんが(説明が長くなりすぎるので)、オイラー法を理解するためにはこれで十分です。
微分の表し方・公式
-
y が x の関数であるとき、「 dy/dx 」「 y′ 」は、どちらも y を x で一階微分(一回だけ微分すること)した式であることを表します
-
x の関数を「 f(x) 」「 g(x) 」で表すことがよくありますが、これを一階微分した形は「 f′(x) 」「 g′(x) 」で表されます
-
「 y′′ 」「 f′′(x) 」「 d2y/dx2 」は、どれも y を x で二階微分(二回だけ微分すること)した式であることを表します
-
{f(x)+g(x)}′=f′(x)+g′(x)
-
定数を微分すると 0
-
x の関数 f(x) があり、 x=a ( a は定数)のとき
f(x)=f(a) (ちなみに f(a) も定数)
4.関数の近似
「近似」とは「すごく似ていること」、「近似する」とは「すごく似ているものを同じものとみなしてしまうこと」だと思ってください。例えば、みなさんが買い物をするときに、税込み 9990 円のお肉があったら、ほぼ 1 万円として計算しますよね。相当ギリギリのお金しかない場合を除いては、ざっくりとした値で合計金額を計算すると思います。これも立派な近似です。
同様に、関数でも近似をしたくなるときがあります。例えば、 f(x) は x の関数であり、 x=a の時の f(x) の値(つまり f(a) )がわかっているとします。この時、「 f(a+0.01) を求めよ」と言われたらどう思いますか?
f(x)にa+0.01 を代入して……という考え方もありますが、多くの人はこの作業を面倒くさがると思います。もちろん数学的に厳密に考えなくてはならない場合は、きちんと計算する必要がありますが、「大体でいいよ~」と言われたら「ほぼ f(a) だよ!」と答えたくなりますよね。これを数学的には、「 f(x) の点 a まわりにおける 0 次近似」と言います。「点 a まわり」とは「 x≒a 」という意味です。
0 次近似では f(x)=f(a) という近似をしました。ですが、近似の精度としてはかなり微妙なのがわかりますか?ざっくりしすぎていて、多くの情報を削ってしまっています。そこで、両辺を x で一階微分をしたときの値も一緒になるように、式をいじってみましょう。こうすれば、グラフの傾きも点 a のまわりでは一致するはずです。
式としては、 f(x)=f(a)+f′(a)(x−a) という形になります。
両辺を微分してみると
f′(x)={f(a)+f′(a)(x−a)}′
f′(x)={f(a)+f′(a)∗x−f(a)∗a}′
f′(x)=f′(a)+{f′(a)∗x}′−{f(a)∗a}′
f′(x)=0+f′(a)−0
f′(x)=f′(a)
点 a まわりでは確かにこの近似が成り立つことがわかります。
一階微分まで考慮した、
f(x)=f(a)+f′(a)(x−a)
という近似を 1 次近似と言います。
さらに正確性を求めていくと、 2 次近似、 3 次近似…と続いていき、無限次近似まですれば、完全に f(x) を多項式の和で表すことができます。これを「テイラー展開」といい、特に原点まわりでのテイラー展開を「マクローリン展開」と言いますが、本記事では深く取り扱うことはしません。大学数学ですので、気になる方は自分で調べてください。
しかし、無限次近似までしないと正確に f(x) の値を表せないにもかかわらず、多くの場合では 1 次近似までで打ち切ってしまいます。なぜでしょうか?参考までに、 2 次近似、 3 次近似は下のようになります。
2 次近似
f(x)=f(a)+f′(a)(x−a)+1/2∗f′′(a)(x−a)2
3 次近似
f(x)=f(a)+f′(a)(x−a)+1/(2!)∗f′′(a)(x−a)2+1/(3!)∗f′′′(a)(x−a)3
さて、それでは 1 次近似までで十分な理由を説明しましょう。注目すべきは (x−a) という部分です。前提として、この近似は x≒a の時に成り立つ近似でしたね。
ということはすなわち、
x−a≒0
が成り立つということです。
2 次近似以降の式では、 (x−a)2 倍、 (x−a)3 倍された項が追加されていますが、 上記より (x−a)2 や (x−a)3 は (x−a) 以上に 0 に近いと言えます。つまり、 1 次近似以降の近似は、どれだけ細かくやったとしても、ほとんど値に変化がないわけです。よって簡単のために、 1 次近似で済まされることが多いのです。
ざっとまとめます。
x の関数 f(x) を点 a まわりで近似した式は
f(x)=f(a)+f′(a)(x−a)
である。
5.オイラー法の気持ち
長々と説明してきましたが、ようやくオイラー法の説明となります。
f(a) の値が与えられるとき、 f(b) の値を求めることを考えてみましょう。
まず、これまでの前提として、 f(a) がわかっているとき、 x≒a のときの f(x) の値を近似することができます。
つまり、刻み幅を h(h≒0) としたとき、 f(a) の値がわかっていれば、 f(a+h) の値を求めることができます。そして、今求めた f(a+h) を使えば、 f(a+2∗h) がわかり、そこから f(a+3∗h) がわかり………をちまちま続けていけば f(b) の値が求められる!!!、というのがオイラー法の考え方です。
式を使ってもう一回言います。
f(a+h)=f(a)+f′(a)∗h
↓
f(a+2∗h)=f(a+h)+f′(a+h)∗h
↓
f(a+3∗h)=f(a+2∗h)+f′(a+2∗h)∗h
↓
・
・
・
↓
f(b)=f(b−h)+f′(b−h)∗h
こういうことです!!これがオイラー法!!!ここまで長かった!!!
6.オイラー法(トイプロの問題)
問題概要
<問題>
y は x の関数, y=f(x)である。
オイラー法を用いて、 f(10) の値を求めよ。
オイラー法は、
f(x+Δx)=f(x)+g(f(x))∗Δx
となっている。
<制約>
- 変数 y0 を入力とする。 y0=f(0) である。(初期条件である。)
-
x の刻み幅は、 Δx=0.01 とする。
- dy/dx=0.5∗f(x)=g(f(x))
- 出力は整数部分のみとする。
解説
一個前の値を持っておけばよいです。要するに、 f(x+Δx) と f(x) の値を常に保持しておけば、次の値を求められます。刻み幅が 0.01 なので、 1000 回ループを回せば 0→10 になりますね。
あとは、式を愚直に実装するだけ、シンプル!
別解
式変形すると、等比数列の漸化式がでてきます。そこから等比数列の一般項を求めることで、答えを求めることも可能です。
7.終わりに
本記事では、簡単のために極限やら関数の連続性やらその他公式定理の説明をすべて端折りました。よって、数学的に厳密には説明できていないと思います。厳密なことは自分で調べるか、大学で教わってください。本記事はその間の架け橋になればと思っています。
感覚的な理解を当初目標として書き始めた記事ですが、最終的には数式的な説明になってしまった気がして、少し反省しています。わからない部分があれば、自分の答えられる範囲で答えるので、遠慮なくコメント残してください。間違いがあればそちらの指摘もお願いします。
以上で解説を終わります。最後まで読んでいただきありがとうございました。

Discussion