「Pythonではじめる数理最適化」を読むぜ
実践的な内容を通じて Python によるデータ分析の雰囲気を掴もうという企み。
第1章 数理モデルとは
1.1 数理モデルの最も簡単な例
現実と数理モデルのギャップを意識することが重要という話。
KPI は改善されているにもかかわらず、まったく目標となる状態に近づいている気がしない
分かりやすいあるある。
1.2 モデル
モデルに含まれる「模型」と「見本」の2つの意味について。
「模型(学力を点数として定量化すること)」と「見本(点数が上がったという事実から学力が向上したと判断すること)」に分けて現実世界とモデルの世界の行き来を図解。
現実に近い数理モデルを構築することは大事だが、それ以上に現実への適用に耐えうることが重要
ふむ。
1.3 数理モデル
数理モデルとは対象を数学によって記述したモデルを指す。
数理モデルは現実世界の複雑な現象を十分な精度で説明できるとは限らない。
その限界を知り、現実への適用は慎重に行う必要があるとのこと。
この点は十分に気をつけないといけないと思った。
1.4 数理最適化モデル
数理最適化モデルの目的は数ある選択肢のなかから最適な選択を見つけること。
経路選択問題やナップサック問題という代表例を通じて数理最適化モデルの利用シーンがイメージできた。
挿絵がかわいい。
ナップサックにお寿司は入れんやろ 🍣🎒
1.5 第1章のまとめ
この章は数理モデルを利用するための重要な心構えを知ることができ、初心者の自分にとっては第1章からいきなり学びの多い章だった。
はじめにこの話をしておいてくれるの最高。
特に 1.2, 1.3 のモデル利用の図解とその限界の話がよかった。
第2章 Python 数理最適化チュートリアル
ここから手を動かすゾーンに突入し、一気にプログラミング色が強くなる。
データは GitHub Repository からダウンロードする。
てか GitHub で ipynb ファイル開くとこんな感じで表示されるんだ…。
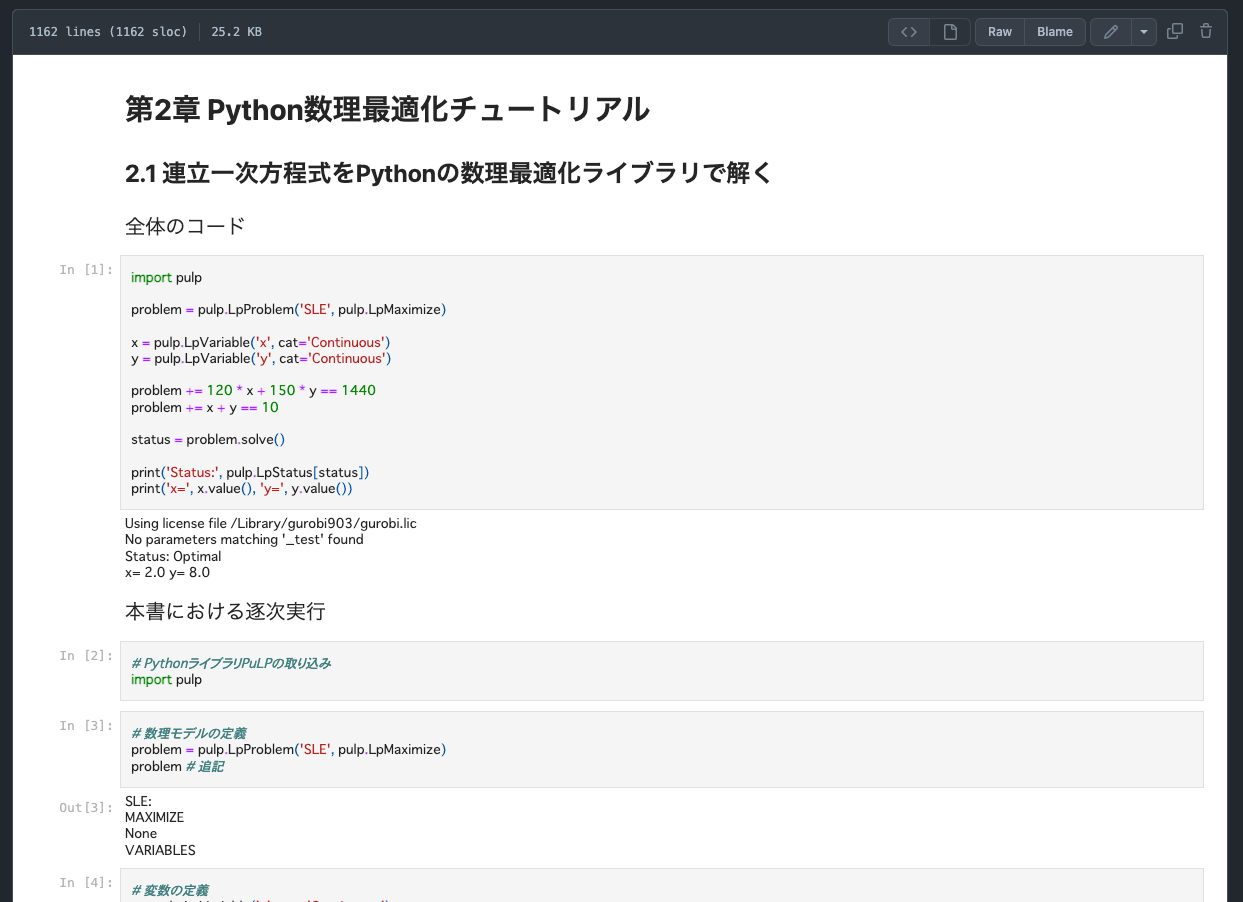
2.1 連立一次方程式を Python の数理最適化ライブラリで解く
数理モデリングには PuLP を使用する。
インストールは各自やっておいてねという感じなのでやっておく
conda list でインストール済みパッケージを表示すると確かに pulp は入っていない。
conda search pulp してみると、PackagesNotFoundError と言われる。
:: Anaconda.org で pulp を検索すると conda-forge/pulp がポピュラーっぽい。
conda install -c conda-forge pulp
これで pulp 2.6.0 がインストールされた。
ちなみに conda-forge とは GitHub 上で組織されているコミュニティ主体のパッケージコレクションで、大体のパッケージはここで見るかるとのこと。
数理モデルに制約式を加える操作を以下のように書けるの凄い。
Python で演算子のオーバーロードできるのね。
x = pulp.LpVariable('x', cat='Continuous')
y = pulp.LpVariable('y', cat='Continuous')
problem += 120 * x + 150 * y == 1440
problem += x + y == 10
2.2 線形計画問題を Python の数理最適化ライブラリで解く
2変数、4制約式の線形計画問題を解いた。
線形計画問題を20行足らずのコードで解けるの凄い。
数理最適化モデルのいくつかのクラス(分類)についてもさらっと触れられている。
2.3 規模の大きな数理最適化問題を Python の数理最適化ライブラリで解く
ここで pandas が初登場。
pandas はデータフレームという2次元の表形式のデータを処理するためのライブラリで、データの入出力や統計処理などが行えるライブラリ。
大規模な線形計画問題では 100 万変数の問題を解くこともある
マジか 😱
数理モデリングするために、リスト・定数・変数を準備したうえで、制約式と目的関数を定義する。
コードが少し複雑になってきた。
ひとつずつゆっくり理解すれば読めるけど、スラスラ読み書きできるには慣れが必要。
また変数を連続変数から整数変数に書き換え、整数計画問題として同じように解くことができた。
2.4 第2章まとめ
この章では pulp, pandas のライブラリを使って線形計画問題を解き、JupyterLab やライブラリの使い方の雰囲気を掴めた。
また整数計画問題は難しく安定して解くことは期待できないため、線形計画問題で解いて解を丸める方法(連続緩和)は実務でも使われる有効な方法ということを知った。
現実的な落とし所だと思った。
第3章 学校のクラス編成
3.1 導入
クラス編成を数理最適化問題にモデリングして解くことで以下のメリットが得られる。
- 最適性
- コスト削減
- 柔軟性
- 公平性
3.2 課題整理
現実の問題を言語化していく過程を眺めている感じ。
実際のクラス運用がうまく回るかを想像しながら編成ルールを定めていくのが重要。
3.3 数理モデリングと実装
ここから motplotlib が初登場。
csv データを pandas で読み込んでデータの内容やヒストグラムなどを確認する。
数理モデルの構築前にデータをイメージしておくことが大事。
その後モデリングを行うが、制約式が非線形となる場合注意が必要になる。
一般に数理最適化問題として定式化する場合、非線形の制約がふくまれると利用できるソルバーが限定されるため、線形の制約に変換可能な場合は迷わず線形に書き換えるのが定石となる。
いろいろ気をつけなきゃいけないことがあるのね。
実装の流れは第2章とさほど変わらず。
相変わらずコードはゆっくり理解すれば読めるが自分で書ける気はしない。
3.4 数理モデルの検証
結果が要件を満たすことをデータやヒストグラムなどを表示して検証する。
テストの点数の分布の偏りを見つけ、制約を追加することにより数理モデルをブラッシュアップする。