時系列データ分析 論文解説②「 PatchTST 」
論文
前回記事 に引き続き、時系列データ分析のための論文紹介になります。
今回は、前回紹介した「Transformer って時系列データで有効なの?」に対して、「いややっぱり Transformer 有効じゃね?」と考え直し、さらに改造を加えた Transformer で有効性を示した論文になります。
タイトル
A TIME SERIES IS WORTH 64 WORDS: LONG-TERM FORECASTING WITH TRANSFORMERS
論文: https://arxiv.org/pdf/2211.14730
Github: https://github.com/yuqinie98/PatchTST
概要
- 多変量(要は Multi Channel, 複数特徴量 )時系列予測および自己教師あり表現学習のための効率的な Transformer ベースモデル、channel-independent patch time series Transformer ( PatchTST ) を提案
- 最先端の Transformer ベースモデルと比較して、長期予測精度を大幅に改善
モデル構造
PatchTST は以下の構造で、Transformer Encoder ブロックに入る手前の Patching と呼ばれる処理が特徴となっています。

Patching
論文でも言及されていますが、この Patching という仕組みは、Vision Transformer から着想を得たものです。ざっくり言うと、時系列長を適当に分割圧縮し、分割された単位で Transformer Encoder に入力します。
こうする事で
- 時系列点群の情報は保持しつつ、時系列長を圧縮でき Attention の計算量を削減.
- それにより、さらに長い時系列点を扱え、長期な時系列予測の精度が上がるはず.
といった効果が期待されます。コードで言うと以下です。
この unfold という処理は以下のようになります。
>>> aa = torch.rand(2, 8)
>>> aa
tensor([[0.7677, 0.6648, 0.4374, 0.8376, 0.4941, 0.2850, 0.2395, 0.8672],
[0.3721, 0.1378, 0.0624, 0.0866, 0.9502, 0.9118, 0.4224, 0.2716]])
>>> aa.unfold(dimension=-1, size=4, step=2)
tensor([[[0.7677, 0.6648, 0.4374, 0.8376],
[0.4374, 0.8376, 0.4941, 0.2850],
[0.4941, 0.2850, 0.2395, 0.8672]],
[[0.3721, 0.1378, 0.0624, 0.0866],
[0.0624, 0.0866, 0.9502, 0.9118],
[0.9502, 0.9118, 0.4224, 0.2716]]])
この Patching を組み合わせた Transformer Encoder までの入力を疑似コードで書いてみる(by ChatGPT)と以下です。
def forward(x): # x: [B, C, L]
B, C, L = x.shape # Batch, Channel, Length (時系列長)
# 1) Instance Norm ※保存して後で元スケールに戻す
mu = mean(x, dim=-1, keepdim=True) # [B, C, 1]
sigma = std (x, dim=-1, keepdim=True) + eps # [B, C, 1]
x_n = (x - mu) / sigma # [B, C, L]
# 2) Patching
# N = パッチ数 = floor((L - P)/S) + 1
patches = unfold1d(x_n, kernel_size=P, stride=S) # [B, C, N, P]
# 3) Projection
# 重みはパッチ次元Pに対する線形: W_patch: [P, d], bias: [d]
tokens = matmul(patches, W_patch) + b_patch # [B, C, N, d]
# 4) Position Embedding
tokens = tokens + PE[:N] # [B, C, N, d], PE: [N, d] broadcast
# 5) Reshape
z_in = tokens.reshape(B*C, N, d) # [B*C, N, d]
# 6) Transformer Encoder
z_enc = transformer_encoder(z_in) # [B*C, N, d]
...
この z_in = tokens.reshape(B*C, N, d) # [B*C, N, d] という処置で reshape を行い、共通部の Transformer Encoder に ( N(パッチ数), d(圧縮後特徴量) ) を入力しています。N x N個の Attention 計算が行われています。
Patching しなければ ( L(時系列長), C(特徴量数) ) で入力されるので、N / L に比例した計算量が削減されていることになります。
Position Embedding
デフォルト設定では以下のような、初期値ランダム一様分布の学習可能なパラメータを Position Embedding として足しているようです。
Flatten + Linear Head
デフォルトでは以下のような Module が適用されています。Transformer の出力に対して、(N, d) を N x d にフラットにし、Linear に入力しています。
※この箇所は、時系列的に最後のパッチのみ使うなど、他にも方法はあります
この Linear で予測対象の時系列点分の数値を予測して、最終的に Instance Norm を元に戻しています。
Loss
MSEで学習。

自己教師あり表現学習
予測タスクへ効果的に転用させるための、自己教師あり表現学習も同時に提案しています。基本的なアイデアは、あるパッチをマスク(値をゼロに変換)し、それを予測するように学習する事です。

コードで言うと上記で、forward の出力z が [bs x num_patch x n_vars x patch_len] for pretrain ( pretrainモードだとこの次元になる ) となっているのが分かります。model の forward の出力はそのまま loss 計算へと反映されるので、つまり、この出力値と Patching 後の生の値を比較して、学習しているという訳です。
直接マスクしている処理は以下です。
- x_masked
マスク後のデータ. モデルへの入力 - x_kept
可視パッチのみの短い系列 - mask
0/1(損失計算で 1 の位置だけ MSE を取る) - ids_restore
復元(unshuffle)用。モデル出力を元順序へ合わせるのに使う
検証方法
データセットなどは論文参照。
まず、100 エポックの自己教師あり事前学習を行います。各データセットで事前学習済みモデルが得られたら、学習された表現を評価するために教師あり学習を実施し、(a) 線形プロービング(linear probing)と (b) エンドツーエンドのファインチューニング(fine-tuning)の 2 つを実施します。
- (a) : ネットワーク本体を凍結し、ヘッドのみを 20 エポック学習
- (b) : (a) を 10 エポック学習してヘッドを更新し、その後ネットワーク全体のパラメータを 20 エポック学習
結果

表にある「Sup.」は事前学習なしの通常の教師あり学習です。みての通り Fine-tuning (b) を行った結果が最良です。
入力時系列長別の結果
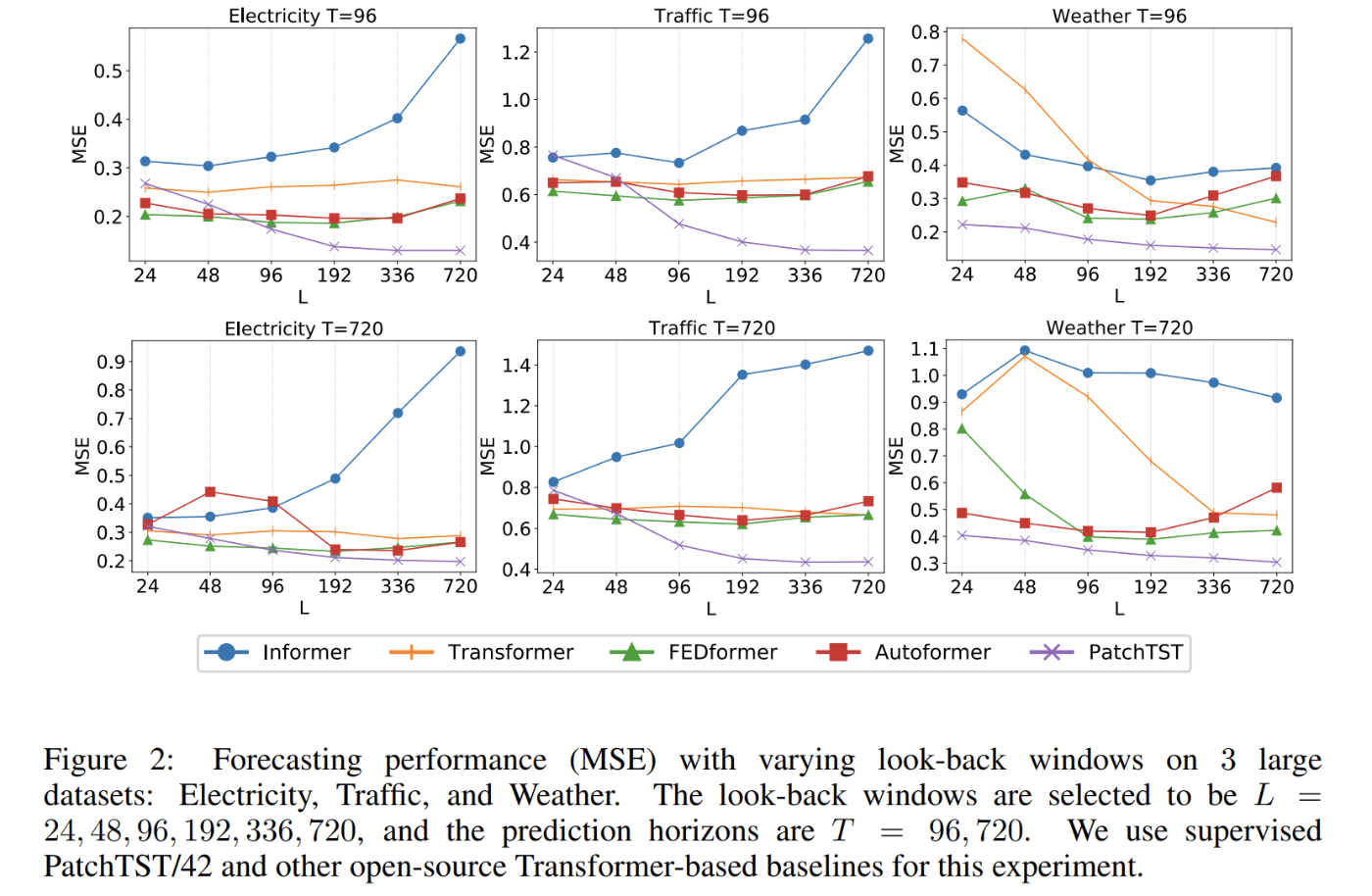
長い時系列長の入力なほど、結果が良くなっています。
考察
基本的には Patching によって能力向上しましたよ、という内容です。Transformer 自体はオリジナルなままなので、入力データを工夫して加工した、って感じです。結果についても、特に不思議はありません(そもそも Transformer という構造が優秀なのは昨今の LLM が示しているからです)。
個人的には
- Position Encoding の有無で結果がどう変わるか
- Fine-tuning という他とは違う条件で精度評価しているので少しズルい
という点が気になります。
Discussion