📖

O'REILLYの「推薦システム実践入門」を読んでのまとめ②

2023/12/20に公開

機械学習

トピックモデル

関連アルゴリズム（つづき）

前回の記事の続きになります。

自然言語処理からの応用

トピックモデル

トピックモデルを使って、コンテンツベース推薦や協調フィルタリングが可能です。

トピックモデルは自然言語処理で幅広く利用されている生成モデルになります。自然言語処理の文脈では、ある文書の集合があった場合に、それぞれの文書にあるトピックがどの割合で混合しているかを分析する事を目的としています。

こういった自然言語を扱う場合、文書をどうにかして数値化する必要があります。そこで登場するのが BOW(bag of words) です。この手法では、文書の内容から単語を抜き出し、それぞれをカウントしてやることで文書をベクトル化します。その文書ベクトルを用いてトピックモデルが作られます。

トピックモデルについては、理解が十分ではないので、解説については割愛させていただきます。

推薦システムにおいては、以下のようにトピックモデルを利用します。まず、以下のようなユーザの行動履歴を取り出します。

User1: [item1, item33, item22, item47, ... ]
User2: [item9, item84, item2, item65, ... ]

これらを単語とみしてカウントし、ユーザの行動履歴をBOWでベクトル化します。その後の流れは自然言語処理の手法と同じです。トピックモデルによって得られた各ユーザのトピック確率分布を用いて、それと類似したトピックに該当するアイテムを推薦するという流れになります。

word2vec

こちらも自然言語処理でよく利用される手法になります。word2vec は単語の分散表現（ベクトル化）を得る事が目的です。word2vec の肝は、ある単語の意味はその周辺の単語に依存する というものです。つまり、単語から周辺単語（もしくは周辺単語から単語）を予測しよう、という流れで単語の意味となるベクトルを得る事を目指します。

word2vec は大きく分けて下記の２つの手法があります。

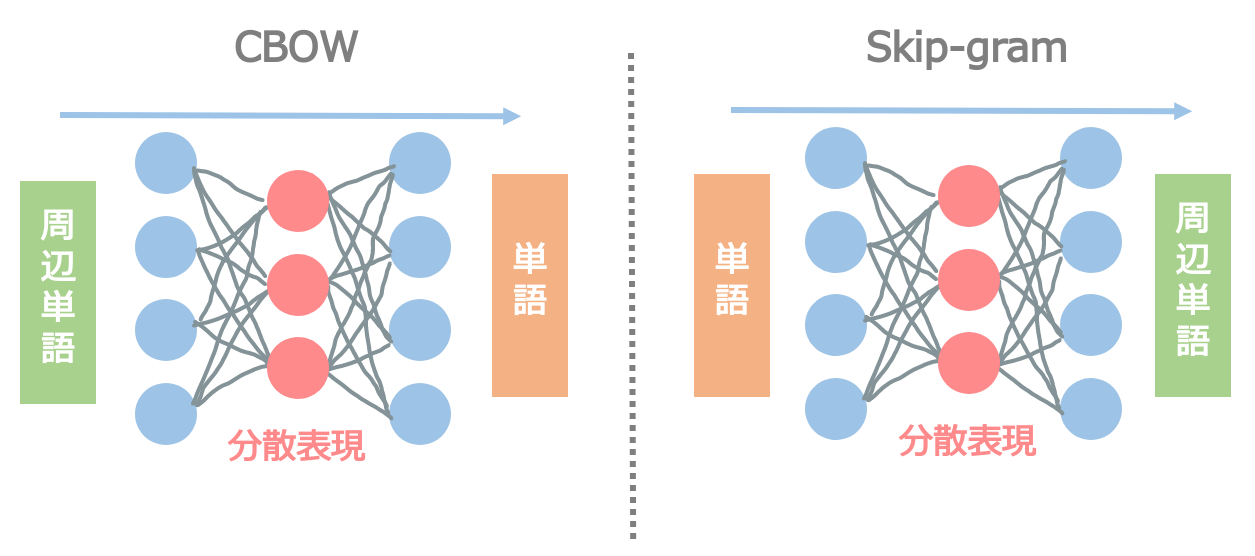
解説の分かりやすさのため、skip-gram を取り上げて説明します。

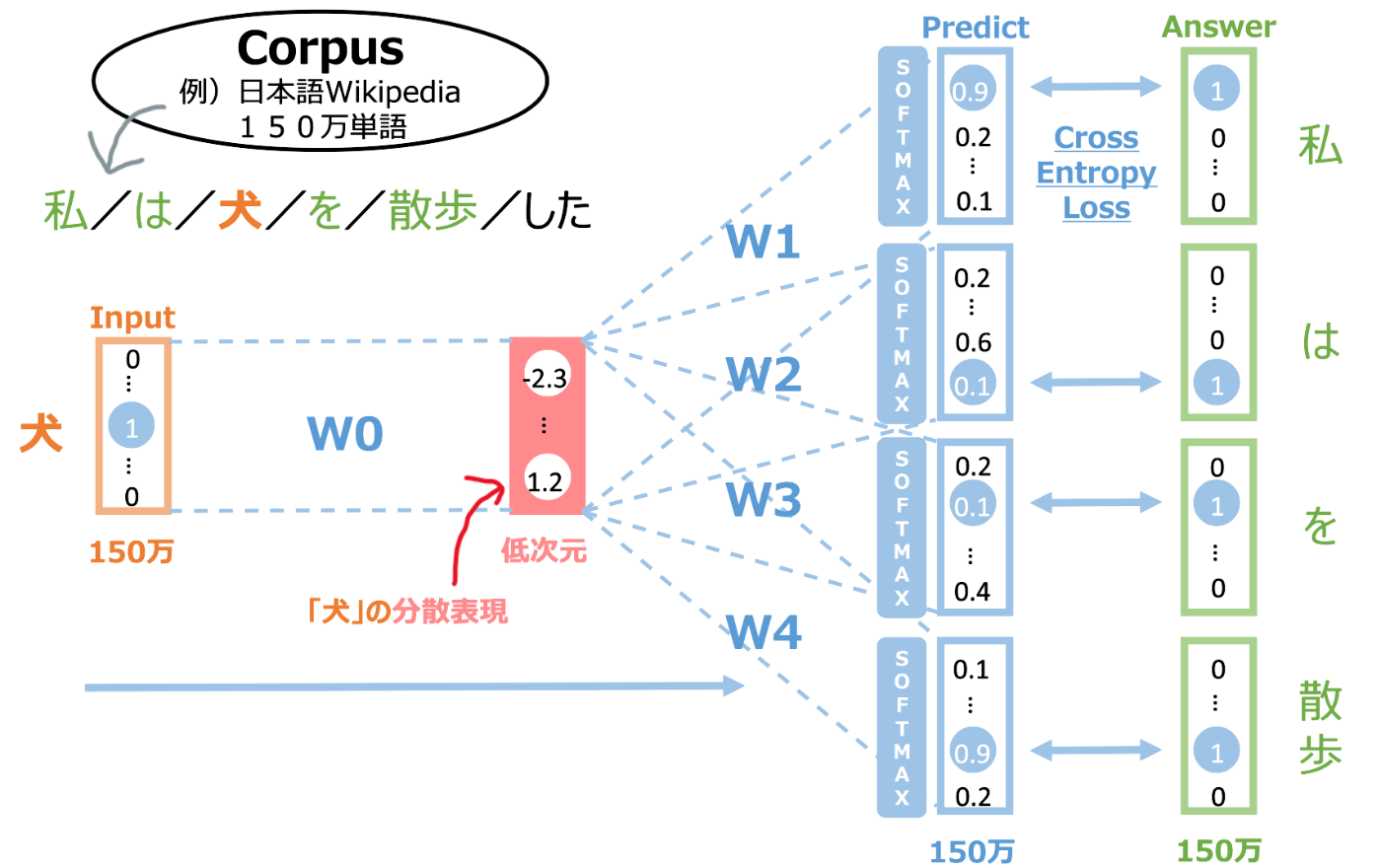
単語の分散表現を得るためにその元となる学習データが必要です。それらは、Corpus と呼ばれます。上図では、例として Wikipedia が学習データです。Wikipedia はおよそ150万単語存在します。

まず、周辺単語の数を決めます。どんな数字が適切かは Corpus に依存するような気もしますが、上図では周辺単語の数は 2 としています。「私は犬を散歩した」という文章があり、「犬」という１単語のインプットから、その周辺の両２単語「私」「は」「を」「散歩」を予測します。アウトプット層は softmax 関数によって確率化され、その値を CrossEntropy で学習します。そうして学習して最終的に得られた中間層（低次元）が、ある単語の分散表現となっています。

単語の各ベクトルを得られると、例えばあるアイテムに含まれる単語をベクトル化して平均化する事で、そのアイテムのベクトルを得る事が可能です。その容量で、似たアイテムを推薦するコンテンツベース推薦が可能となります。

Item2vec

word2vec の応用です。学習データとして、文章では無く、以下のようなアイテムの視聴/購入といった行動履歴を使います。

User1: [item1, item33, item22, item47, ... ]
User2: [item9, item84, item2, item65, ... ]

学習方法は同様で、これらを学習する事で、各アイテムのベクトルを得る事が可能です。つまり、例えば item22 を入力として周辺の item33 や item47 を予測する事を繰り返して学習します。このベクトルを用いて同様に推薦を行いますが、こちらは実はアイテムの中身には全く触れておらず、ユーザーの行動履歴から学習しているため、協調フィルタリングとなります。

深層学習

ここでは、本で紹介されてる深層学習系の手法について紹介します。また本で紹介されていた有名なライブラリを載せておきます。

Neural Collaborative Filtering

論文はこちらです。構造の絵は以下になります。

Neural collaborative filtering framework^[1]

非常に分かりやすく、単純に user_id, item_id を One-Hot ベクトルで表現し、それらを Embed して層を重ねたモデルになっています。

DeepFM

DeepFM は Factorization Machines を深層学習化した手法になります。少し論文の絵が個人的に難しく、結局実装ベースで内容を理解しました。

論文の絵では各特徴量の結合が複雑で、実装の流れをベースに全体の計算を絵にしました。ちょっと画像の粒度が粗いのでこの後に各部分で確認しますが、計算の値の種類としては、３種類の数値を計算しています（画像内のA,B,Cに当たる箇所）。

カテゴリ特徴量の前段処理

DeepFM は FM 同様、カテゴリカルな特徴量や連続値について処理が可能です。まずは、カテゴリカルな特徴量に対して Embed する前段処理を確認します。実装ではこの箇所です。

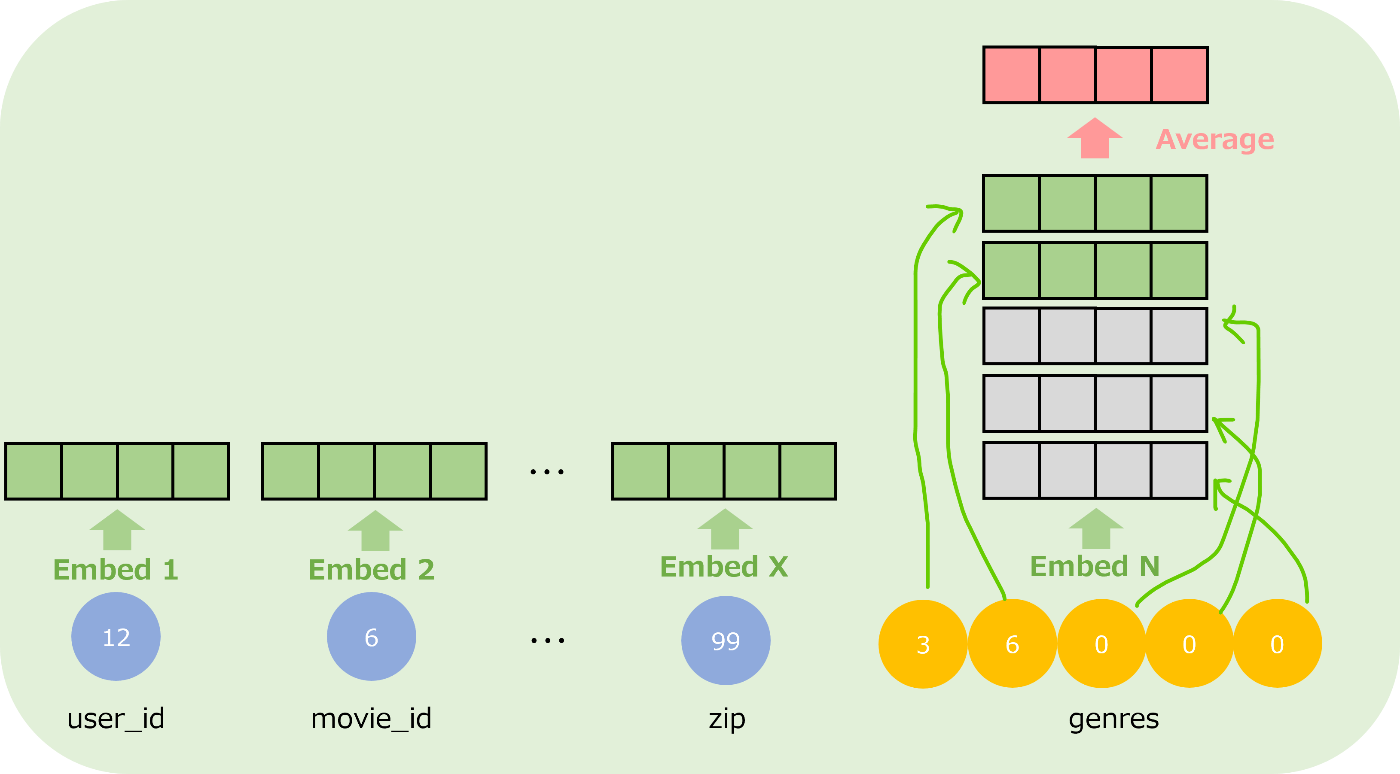
ここで、２種類のカテゴリ値が存在します。１つはユーザーIDや映画IDや性別など一つのIDとして持てるもの（単一IDと呼ぶ）、もう一つは映画のジャンルなどあるジャンルIDを複数所持できるもの（複数IDと呼ぶ）、です。

各特徴量の種類の数だけ Embed するレイヤーを用意します。カテゴリ値が7個あれば、Embed レイヤーは7個用意されます。Embed 先の次元数 $k$ はハイパーパラメータです（絵では $k=4$ ）。複数IDについては、例えば絵の genres は５種類までのジャンルを持つ事ができます（3,6,0,0,0）が、ジャンルIDは共通なので、genres について１つの Embed レイヤー（Embed N）を用意します。そして、ジャンルが有効な箇所だけ（3 と 6 の Embed 値）で平均（や加算）を行います。

このようにして、各カテゴリ特徴量から固定長のベクトルに Embed します。そして、この特徴量を使って FM(A) と DNN(B) を計算します。

FM (A)

Aパートです。実装ではこの箇所です。

前段処理パートで得られた各カテゴリ特徴量の Embed を、「足して二乗したベクトル」－「二乗して足したベクトル」で得られたベクトルをさらに全部足して、スカラー値Aを得ています。絵にはかいていませんが、最後に 0.5 を掛けています。

DNN (B)

Bパートです。実装ではこの箇所です。

前段処理パートで得られた各カテゴリ特徴量の Embed を全て横に並べて、さらに連続値の特徴量も横に追加したベクトルを用意します。例えばもともとの特徴量が UserID(単一ID), MovieID(単一ID), Genres(複数ID), 視聴時間(連続値), 視聴回数(連続値) といった５種類の特徴量を k=4　次元に Embed する場合、全て横に並べた後の次元数は 4+4+4+1+1 = 14 となります。

その特徴量をFFN（feedforward network）で計算します（絵に書いていませんが、活性化関数やドロップアウトは普通に使われています）。最終的にスカラー値Bを得ます。

Linear (C)

Cパートです。実装ではこの箇所です。

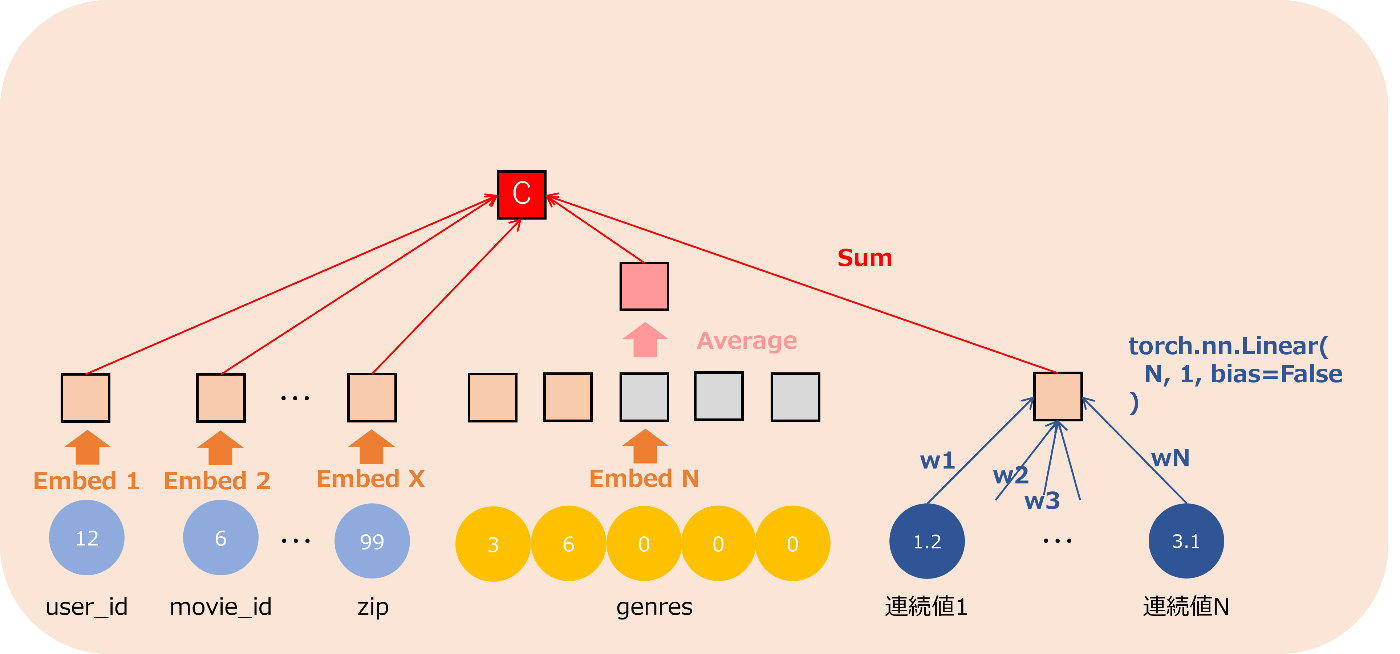
ここでは前段処理パートとは別の計算になります。計算は前段処理パートと似ています。カテゴリ特徴量に関して、Embed 先の次元数が 1 以外は同じ計算をします。連続値特徴量は、それらだけの値を使い、線形回帰をします（この時バイアス値はありませんでした）。そして、それらを全て足す事によって、最終的にスカラー値Cを得ます。

予測値の計算

スカラー値を足して、Sigmoid で計算します。

今回の例では二値分類が目的のためこのような予測値となっていますが、目的関数によって計算が変わると理解しています。

実装ベースの確認

コードベースで確認したので、少し細かくなりますが、詳細を確認したい方は以下を確認してください。

python code

movielens_sample.txt の中身

>>> data
     user_id  movie_id  rating  timestamp                                        title                     genres gender  age  occupation    zip
0       3299       235       4  968035345                               Ed Wood (1994)               Comedy|Drama      F   25           4  19119
1       3630      3256       3  966536874                         Patriot Games (1992)            Action|Thriller      M   18           4  77005
2        517       105       4  976203603        Bridges of Madison County, The (1995)              Drama|Romance      F   25          14  55408
3        785      2115       3  975430389  Indiana Jones and the Temple of Doom (1984)           Action|Adventure      M   18          19  29307
4       5848       909       5  957782527                        Apartment, The (1960)               Comedy|Drama      M   50          20  20009
..       ...       ...     ...        ...                                          ...                        ...    ...  ...         ...    ...
195     1427      3596       3  974840560                               Screwed (2000)                     Comedy      M   25          12  21401
196     3868      1626       3  965855033                       Fire Down Below (1997)      Action|Drama|Thriller      M   18          12  73112
197      249      2369       3  976730191             Desperately Seeking Susan (1985)             Comedy|Romance      F   18          14  48126
198     5720       349       4  958503395              Clear and Present Danger (1994)  Action|Adventure|Thriller      M   25           0  60610
199      877      1485       3  975270899                             Liar Liar (1997)                     Comedy      M   25           0  90631

[200 rows x 10 columns]

以下では、gender を 0,1 で表現して、user_id, movie_id, age, zip について 0 index 始まりにして修正しています。

>>> data
     user_id  movie_id  rating  timestamp                                        title                     genres  gender  age  occupation  zip
0        107        12       4  968035345                               Ed Wood (1994)               Comedy|Drama       0    2           4   35
1        123       169       3  966536874                         Patriot Games (1992)            Action|Thriller       1    1           4  118
2         12         6       4  976203603        Bridges of Madison County, The (1995)              Drama|Romance       0    2          13   99
3         21       112       3  975430389  Indiana Jones and the Temple of Doom (1984)           Action|Adventure       1    1          18   55
4        187        45       5  957782527                        Apartment, The (1960)               Comedy|Drama       1    5          19   41
..       ...       ...     ...        ...                                          ...                        ...     ...  ...         ...  ...
195       46       176       3  974840560                               Screwed (2000)                     Comedy       1    2          11   48
196      131        89       3  965855033                       Fire Down Below (1997)      Action|Drama|Thriller       1    1          11  113
197        4       125       3  976730191             Desperately Seeking Susan (1985)             Comedy|Romance       0    1          13   83
198      181        15       4  958503395              Clear and Present Danger (1994)  Action|Adventure|Thriller       1    2           0  106
199       25        86       3  975270899                             Liar Liar (1997)                     Comedy       1    2           0  136

[200 rows x 10 columns]

gender_list は次のようになっていて、これは最大５個までジャンルを格納できる配列です。配列の中身はジャンルの index になっています。0番目の値は、単に１つめのジャンル、という意味です。

>>> genres_list[:10]
array([[1, 2, 0, 0, 0],
       [3, 4, 0, 0, 0],
       [2, 5, 0, 0, 0],
       [3, 6, 0, 0, 0],
       [1, 2, 0, 0, 0],
       [1, 0, 0, 0, 0],
       [7, 1, 0, 0, 0],
       [2, 0, 0, 0, 0],
       [2, 0, 0, 0, 0],
       [8, 0, 0, 0, 0]], dtype=int32)
>>> genres_list.shape
(200, 5)

その他変数

>>> fixlen_feature_columns
[SparseFeat(name='movie_id', vocabulary_size=187, embedding_dim=4, use_hash=False, dtype='int32', embedding_name='movie_id', group_name='default_group'), SparseFeat(name='user_id', vocabulary_size=193, embedding_dim=4, use_hash=False, dtype='int32', embedding_name='user_id', group_name='default_group'), SparseFeat(name='gender', vocabulary_size=2, embedding_dim=4, use_hash=False, dtype='int32', embedding_name='gender', group_name='default_group'), SparseFeat(name='age', vocabulary_size=7, embedding_dim=4, use_hash=False, dtype='int32', embedding_name='age', group_name='default_group'), SparseFeat(name='occupation', vocabulary_size=20, embedding_dim=4, use_hash=False, dtype='int32', embedding_name='occupation', group_name='default_group'), SparseFeat(name='zip', vocabulary_size=188, embedding_dim=4, use_hash=False, dtype='int32', embedding_name='zip', group_name='default_group')]
>>> varlen_feature_columns
[VarLenSparseFeat(sparsefeat=SparseFeat(name='genres', vocabulary_size=18, embedding_dim=4, use_hash=False, dtype='int32', embedding_name='genres', group_name='default_group'), maxlen=5, combiner='mean', length_name=None)]
>>> key2index
{'Comedy': 1, 'Drama': 2, 'Action': 3, 'Thriller': 4, 'Romance': 5, 'Adventure': 6, "Children's": 7, 'Western': 8, 'Horror': 9, 'Fantasy': 10, 'Sci-Fi': 11, 'Animation': 12, 'Crime': 13, 'Film-Noir': 14, 'Musical': 15, 'War': 16, 'Mystery': 17}

Wide & Deep

Google から発表されている手法です。論文

The spectrum of Wide & Deep models^[2]

この絵の左側が Wide に線形結合した時、右側がカテゴリ特徴量を Embed して Deep に積み重ねた時、真ん中が本論文の手法となっています。

そして実際は以下の構成で検証されています。

Wide & Deep model structure for apps recommendation^[3]

この論文中の「Cross Product Transformation」が実際によく分からない箇所ではあるのですが、この Kaggle の notebook を確認したところ、過去視聴した映画の binary 表現が論文中の $\phi$ に当たる変数として使われていました。例えば、全映画が100種類あり、あるユーザが20番目と40番目の映画を視聴している場合、100次元あるベクトルの20番目と40番目が　1 でそれ以外は 0 といった値が入っています。

[0, 0, ..., 1, ..., 1, ..., 0, 0]

この投稿でも似たような議論がありました。しかしながら詳細は良く分かりません。

バンディッドアルゴリズム

本記事と同列に紹介するには内容が重すぎるのと難しすぎるので諦めます。

実システムへの応用

実際のシステム設計についてまとめられた章です。ここでは一部抜粋します。

多段階推薦

多くのユーザーを抱えるサービスにおける推薦では、システムの負荷を考慮した設計が不可欠です。そのため、その推薦のためのステップを分け、精度はざっくりでいいからとにかく計算を早くするところや、ある程度絞られた候補について精度良く計算すべきところ、などいくつかのステップがあります。

多段階推薦^[4]

候補選択

例えば、YouTube では数十億の動画が貯まっており、この段階で推薦アイテム候補を100～10,000個に削減します。この候補選択の処理は、膨大なアイテムに対して実行する必要があるため処理の軽さが求められます。

スコアリング

スコアリングは、実際にユーザーに掲出するアイテムを選択するために、アイテムに対してスコアを与える処理です。このスコアリング処理では、候補選択によってスコアリング対象が十分削減されているので、負荷の高いモデル、特に機械学習モデルによる高精度な推論を活用することが多いです。

リランキング

スコアリングで選択されたアイテムを並び替える処理を行います。ここでは、ランキング全体のバランスを考慮して似通ったアイテムばかり並ばないようにする処理や、アイテムの鮮度を考慮して並び替える処理を行います。Google検索などの結果の並び順に相当する処理ですかね。

近似最近傍探索

内容ベースフィルタリングなどで類似のアイテムを検索する場合、それらアイテムは多くの場合、前述のアルゴリズムによってベクトル化されているはずです。その際、あるアイテムAのベクトルに対して「最近傍探索」を行うと、アイテムAに類似したアイテムXが見つかるはずです。

しかし、アイテムが大量にある場合は、この「最近傍探索」に時間がかかります。そこで登場するのが「近似最近傍探索」です。「近似」と付いているように、一部正確性を犠牲にして、入力されたベクトルに近いベクトルを高速に探し出す方法です。

近似最近傍探索（approximate nearest neighbor）のベンチマークを載せておきます。

Performance of approximate nearest neighbor approaches^[5]

評価指標

本に書かれてある神表^[6]を引用します。

指標の分類	利用目的	代表的な指標
予測誤差指標	学習モデルがどれほどテストデータの評価値に近い予測が<できるかを測る。	MAE MSE, RMSE
集合の評価指標	モデルが出力したスコアの高いk個のアイテム集合に関する抽出能力を測る。クリックや購買の有無などの二値分類の精度の評価や、推薦の幅広さを測るために利用される。	Precision Recall F1-measure
ランキング評価指標	アイテムの順序を考慮したランキングの評価に用いられる。モデルが出力したスコアの高いk個のアイテムがどれほど正しく並んでいるかを測る。	nDCG MAP MRR
その他の評価指標	クリックの有無のような予測精度以外で、ユーザーの満足度を間接的に測る。	カバレッジ多様性新規性セレンディピティ

RMSEなどの良く知られた指標は割愛しますが、いくつかの指標について下記で説明します。

Precision（適合率）

予測したもののうち、実際に正解だったものは何割か、という指標です。例えば二値分類タスクの場合、正解ラベルが 0 か 1 で、あるデータが 0 か 1 かを予測します。その場合は単純に

1予測の中の1正解の数 / 1予測数

となります。

ランキングなど、予測が多数の場合は次のように計算できます。まずデータとして次のようなデータが与えられている場合

# 予測アイテム集合（例えば特定の検索ワードにおける推薦記事の上から順）。予測スコアの高い順に並べる
pred_items = [1, 2, 3, 4, 5]
# 適合アイテム集合（例えばあるユーザが同じ検索ワードを用いて検索を行い同じ記事が推薦された場合の、実際にクリックした記事のインデックス。この場合４回クリックした）
true_items = [2, 4, 6, 8]

Precision@K は以下のように計算できます。

Precision@K=\cfrac{|C\bigcap R_K|}{K}

$C$ は適合アイテム集合、 $K$ はランキングの長さ、 $R_K$ は予測アイテム集合の $K$ 番目以内のアイテムを表します。この時、 $Precision@3=1/3$ 、 $Precision@4=2/4$ となります。 $K=3$ の時は、pred_items が [1, 2, 3] しか見えていない状態で、true_items = [2, 4, 6, 8] と比較するという事になります。

Recall（再現率）

同様に Recall について考えます。二値分類においては、

1正解の中の1予測の数 / 1正解数

となり、正解の中でどれだけ正しく予測する事ができるか、となります。ランキングなどのデータにおいては

Recall@K=\cfrac{|C\cap R_K|}{C}

となります。同じデータ例を用いると、 $Recall@3=1/4$ となります。

PR曲線

似たような指標に ROC 曲線があるかと思いますが、PR曲線はより不均衡なデータに対して使われるようです。

Precision と Recall のプロット^[7]

この下図の AUC(Area Under Curve) の面積を計算したものが、PR-AUC の値となります。

MRR@K（Mean Reciprocal Rank）

こちらは初めて見る指標でした。

MRR@K=\cfrac{1}{|U|}\sum_{u\in U}\cfrac{1}{k_u}

ここで、 $U$ はユーザー全体の集合、 $k_u$ はランキング $K$ 番目以内の最初の適合位置を表します。この記事が理解の役に立ちました。要は、提示した推薦ランキングは、各ユーザにとってどの程度正しかったのか、の指標になり得ます。実際にユーザが求めていたアイテムや記事が、推薦されたランキングの下位に属していた場合、指標は悪くなります。

AP@K（Average Precision）

AP(u)@K=\cfrac{1}{\sum_{k=1}^{K}c_{u,k}}\sum_{k=1}^{K}c_{u,k}\times Precision@k

$K$ はランキングの長さ、 $c_{u,k}$ はユーザー $u$ の $k$ 番目のアイテムが適合する時に 1、それ以外で 0 となります。同じデータ例で値を求めると、

AP@5=(0\times Precision@1 + 1\times Precision@2 + 0\times Precision@3 + 1\times Precision@4 + 0\times Precision@5) / (0+1+0+1+0)\\ = (1/2 + 2/4) / 2 = 0.5

ここでの Average は特定のユーザにとっての、という意味です。

MAP@K（Mean Average Precision）

MAP@K=\frac{1}{|U|}\sum_{u\in U}AP(u)@K

MAP は AP を各ユーザーに対して平均をとった値になります。

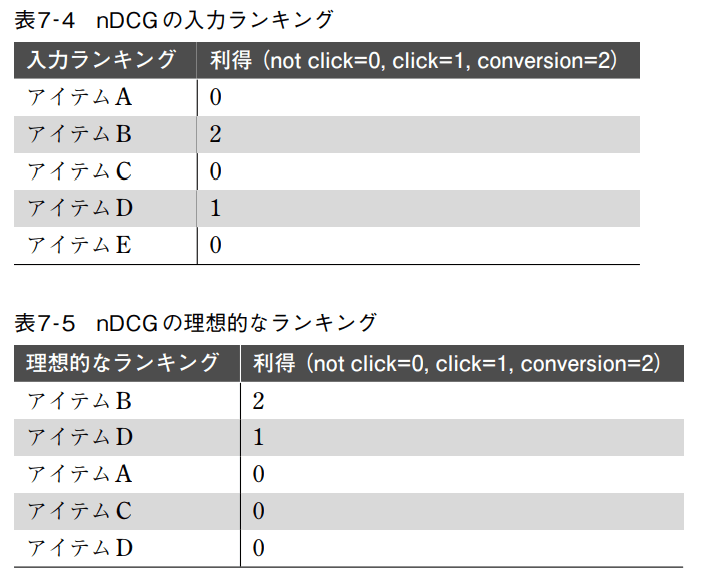
nDCG（normalized Discounted Cumulative Gain）

上記の指標では、クリックの有無のような二値に対する指標でしたが、もしかしたらクリック以外のアクションによって得られる利得も考慮に入れた計算をしたいかもしれません。そこで登場するのが $nDCG$ 及び $DCG$ という指標です。

nDCG@K=\frac{DCG@K}{DCG_{ideal}@K}

DCG@K=r_1+\sum_{i=2}^{K}\frac{r_i}{\log_{2}i}

$K$ はランキングで $r_i$ は i番目のランキングでの利得を表します。例えば、ユーザーがアイテムをクリックしたときの利得を1、さらに購入したときの利得を2、クリックしない場合を0とたときのデータが以下のようになったとします。

^[8]

このときの $nDCG@5$ は

DCG@5=0+\frac{2}{\log_{2}2}+\frac{0}{\log_{2}3}+\frac{1}{\log_{2}4}+\frac{0}{\log_{2}5}=2.5 \\ DCG_{ideal}=2+\frac{1}{\log_{2}2}+\frac{0}{\log_{2}3}+\frac{0}{\log_{2}4}+\frac{0}{\log_{2}5}=3.0

nDCG=\frac{DCG@5}{DCG_{ideal}@5}=2.5/3.0

となります。

新規性（Novelty）

Novelty(R)=\frac{\sum_{i\in R}-\log_2 p(i)}{|R|} \\ p(i)=\frac{\sum_{u\in U} imp(u,i)}{|U|}

imp(u,i)= \begin{cases} 1 &: ユーザuにアイテムiが過去に推薦された場合 \\ 0 &: それ以外 \end{cases}

$R$ はランキング、 $U$ はユーザの集合を表します。新規性が高い場合、 $p(i)$ の確率は下がり、 $-\log_{2}p(i)$ の値は大きくなり、結果として $Novelty(R)$ は高くなります。

多様性（Diversity）

Diversity(R)=\frac{\sum_{i\in R}\sum_{j\in R\ i\neq j}sim(i,j)}{|R|(|R|-1)}

$sim(i,j)$ はアイテム $i$ とアイテム $j$ の類似度の距離を表します。類似度の距離が遠い場合、 $sim(i,j)$ は大きくなり、 $Diversity(R)$ は大きくなります。

最後に

ここまでで、自分なりにまとめたい本の内容については、いったん終了です。本で紹介されているアルゴリズムについては歴史的な背景を交えて説明されているため、その理解は大変重要な事ですが、現在主流なモデルとは一致していない可能性があります。次回は、本で取り上げられていない発展的なモデルについて、まとめてみたいと思います。

私は主にアルゴリズムについて興味があり、それを主体として取り上げさせていただきましたが、本の内容は超実践的な内容になっており、システム設計を含めた網羅的な内容となっています。冒頭でも述べましたが、この記事を読むよりも、本を読む方が遥かに意味があります。なので是非、実際の本を手にとってください。とても平易な文章で書かれており、実際のコードも書かれており、とてもオススメです。

PS. この本で改めてトピックモデルやバンディッドアルゴリズムに触れて、いかに自分がベイズ推論を理解していないかを思い知らされました。そちらについてもどこかで記事にしたいと思います。。。

脚注

Neural Collaborative Filtering: Figure 2 ↩︎
論文: Figure 1: The spectrum of Wide & Deep models. ↩︎
論文: Figure 4: Wide & Deep model structure for apps recommendation. ↩︎
推薦システム実践入門 P181 図6-9 ↩︎
Leveraging Reinforcement Learning for evaluating Robustness of KNN Search Algorithms: Figure 3 ↩︎
推薦システム実践入門 P201: 表7-2 代表的な評価指標 ↩︎
推薦システム実践入門 P206: 図7-3, 図7-4 ↩︎
推薦システム実践入門 P211: 表7-4, 表7-5 ↩︎

関連アルゴリズム（つづき）

自然言語処理からの応用

トピックモデル

word2vec

Item2vec

深層学習

Neural Collaborative Filtering

DeepFM

カテゴリ特徴量の前段処理

FM (A)

DNN (B)

Linear (C)

予測値の計算

実装ベースの確認

Wide & Deep

バンディッドアルゴリズム

実システムへの応用

多段階推薦

候補選択

スコアリング

リランキング

近似最近傍探索

評価指標

Precision（適合率）

Recall（再現率）

PR曲線

MRR@K（Mean Reciprocal Rank）

AP@K（Average Precision）

MAP@K（Mean Average Precision）

nDCG（normalized Discounted Cumulative Gain）

新規性（Novelty）

多様性（Diversity）

最後に

Discussion