🔙
AIと読む「Inferring neural activity ~ beyond backpropagation」②

2025/02/18に公開
前回からの続きです。
https://zenn.dev/tanegoma/articles/9d6341f0a49af2

 結果
 展望的構成：直感的な例最適な行動を計画するためには、脳が将来の刺激を予測することが重要であり、例えば、他のモダリティに基づいてあるモダリティの感覚を予測することなどです[^22]。観察された結果が予測と異なる場合、ネットワーク全体の荷重を更新して、「出力」ニューロンの予測が修正されるようにする必要があります。バックプロパゲーションは、出力のエラーを最小限に抑えるために荷重をどのように変更すべきかを計算し、この荷重更新により、ネットワークが次に予測を行うときに神経活動が変化します。対照的に、本稿では、神経活動が最初に新しい構成に調整され、出力ニューロンが観察された結果（ターゲットパターン）をより良く予測できるようにすると提案します。次に、荷重が変更されて、この神経活動の構成が強化されます。この神経活動の構成を「展望的」と呼ぶのは、観察された結果を正しく予測するためにネットワークが生成すべき神経活動であるためです。提案された展望的構成のメカニズムと一致して、予測の結果を提示すると神経活動に変化が引き起こされることが生物学的ニューロンで広く観察されています。例えば、動物にジュースの配達を予測させるタスクでは、報酬は味覚皮質だけでなく、複数の皮質領域でも急速な活動の変化を引き起こします[^23],[^24]。
バックプロパゲーションと展望的構成の違いを強調するために、簡単な例を考えてみましょう（図1a）。クマが川を見ていると想像してください。クマの心の中で、その光景は、水の音を聞き、鮭の匂いを嗅ぐという予測を生み出します。その日、クマは確かに鮭の匂いを嗅ぎましたが、おそらく耳の怪我のために水の音を聞きませんでした。したがって、クマは音に関連する期待を変更する必要があります。バックプロパゲーション（図1b）は、負のエラーを逆伝播して、視覚ニューロンと聴覚ニューロンの間の経路の荷重を減らすことによって進行します。ただし、これは、鮭の匂いが存在し、正しく予測されたにもかかわらず、次に川を訪れたときに鮭の匂いを嗅ぐという期待を損なう、視覚ニューロンと嗅覚ニューロンの間の荷重の減少も伴います。バックプロパゲーションによる学習のこれらの望ましくない非現実的な副作用は、新しい関連付けを学習すると、以前に学習した記憶が破壊されるという壊滅的な干渉の現象と密接に関連しています[^16]。この例は、バックプロパゲーションでは、関連付けの1つの新しい側面を学習するだけでも、同じ関連付けの他の側面の記憶を妨げる可能性があることを示しています。
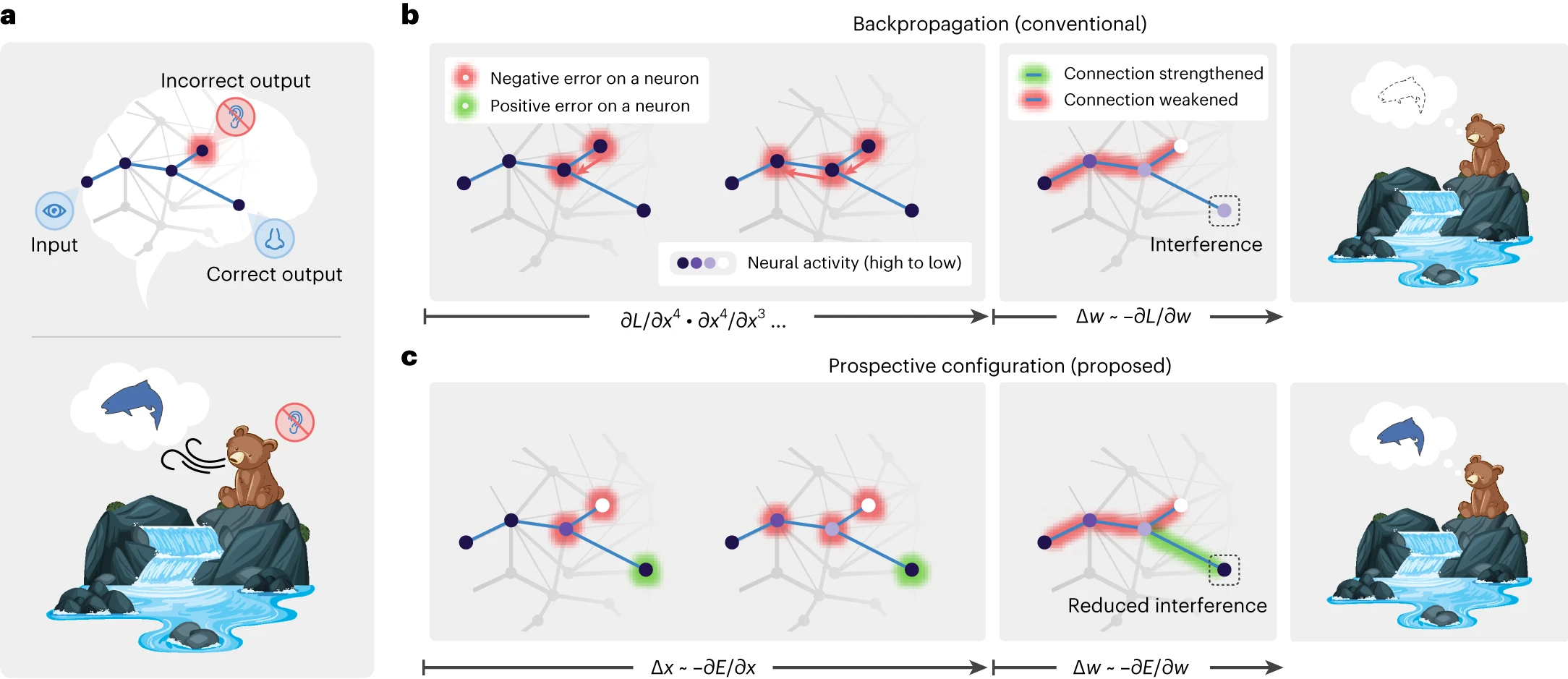
図1 | 展望的構成は学習中の干渉を回避する。

a, 学習中に干渉を引き起こすタスクの抽象的な例（上）と具体的な例（下）。1つの刺激入力（水を見ること）は、2つの予測出力（水の音を聞くことと鮭の匂いを嗅ぐこと）をトリガーします。一方の出力は正しく（鮭の匂いを嗅ぐこと）、他方の出力はエラーです（水の音を聞かないこと）。

b,c, バックプロパゲーションは学習中に干渉を引き起こします。水の音を聞かないことは、鮭の匂いを嗅ぐという期待を減らします（b）。ただし、鮭の匂いは実際に嗅ぎました。一方、展望的構成はそのような干渉を回避します（c）。バックプロパゲーションでは、負のエラーがエラー出力から隠れニューロンに伝播します（b; 左）。これにより、一部の接続が弱まり、次の試行では不正解の出力が改善されますが、正解の出力の予測も減少し、干渉が発生します（b; 中央と右）。展望的構成では、荷重修正の前に神経活動が新しい構成（紫色の強度が異なる）に落ち着きます（c; 左）。この構成は、学習後に生成されるはずの活動に対応します。つまり、「展望的」です。したがって、正しい出力に対する正のエラーを予見し、不正解の出力を改善しながら、正しい出力を維持するように接続を修正します（c; 中央と右）。
対照的に、展望的構成は、学習がニューロンが新しい状態に構成されることから始まることを前提としており、これはネットワークが観察された結果を正しく予測できるパターンに対応します。次に、荷重が変更されて、この状態が強化されます。この動作は、潜在的な荷重変更の副作用を「予見」し、それらを動的に補正できます（図1c）。不正解の出力に対する負のエラーを修正するために、隠れニューロンはその活動が低い展望的状態に落ち着き、その結果、正のエラーが明らかになり、正しい出力に割り当てられます。その結果、展望的構成は、正しい出力に接続する荷重を増加させますが、バックプロパゲーションは増加させません（図1b,c）。したがって、展望的構成は、関連付けの学習の副作用を効果的かつ効率的に、そしてほとんど干渉なしに修正することができます。

 展望的構成の起源：エネルギーベースのネットワーク展望的構成がエネルギーベースのネットワークで自然にどのように発生するかを示すために、物理的な機械のアナロジーを紹介します。これにより、エネルギーベースのネットワークと、それが展望的構成のメカニズムをどのように生成するかを直感的に理解できます。
エネルギーベースのネットワークは、生物学的ニューラルシステムを記述するために広く使用され、成功を収めています[^17],[^25]。これらのモデルでは、ニューラル回路は、ニューロンによって行われたエラーを反映する抽象的な「エネルギー」を削減することによって駆動される動的システムによって記述されます（方法）。神経活動と荷重は、このエネルギーを削減するために変化します。したがって、それらは動的システムの「可動部品」と見なすことができます。エネルギーベースのネットワークは、物理的な機械（「エネルギー機械」と呼びます）と数学的に等価であることを示します。この機械では、エネルギー関数は直感的な解釈を持ち、そのダイナミクスは簡単です。エネルギー機械は、単にその可動部品を調整してエネルギーを削減します。
エネルギー機械には、ロッドとスプリングを介して互いに接続された垂直の支柱上をスライドするノードが含まれます（図2a,b）。エネルギーベースのネットワークからエネルギー機械への変換では、神経活動はソリッドノードの垂直位置にマップされ、接続は、あるノードから別のノードを指すロッド（青い矢印）にマップされます（ここで、荷重はロッドの終端位置が初期位置にどのように関連するかを決定します）。また、エネルギー関数は、両端にノードが取り付けられたスプリングの弾性ポテンシャルエネルギーにマップされます（スプリングの自然長は0です）。異なるエネルギー関数とネットワーク構造は、異なるエネルギーベースのネットワークをもたらし、ノード、ロッド、スプリングの異なる構成と組み合わせを持つエネルギー機械に対応します。図2では、予測符号化ネットワーク[^12],[^18]のエネルギー機械を示します。これは最もアクセスしやすく、バックプロパゲーションと密接に関連していることが確立されているためです[^12],[^14]。
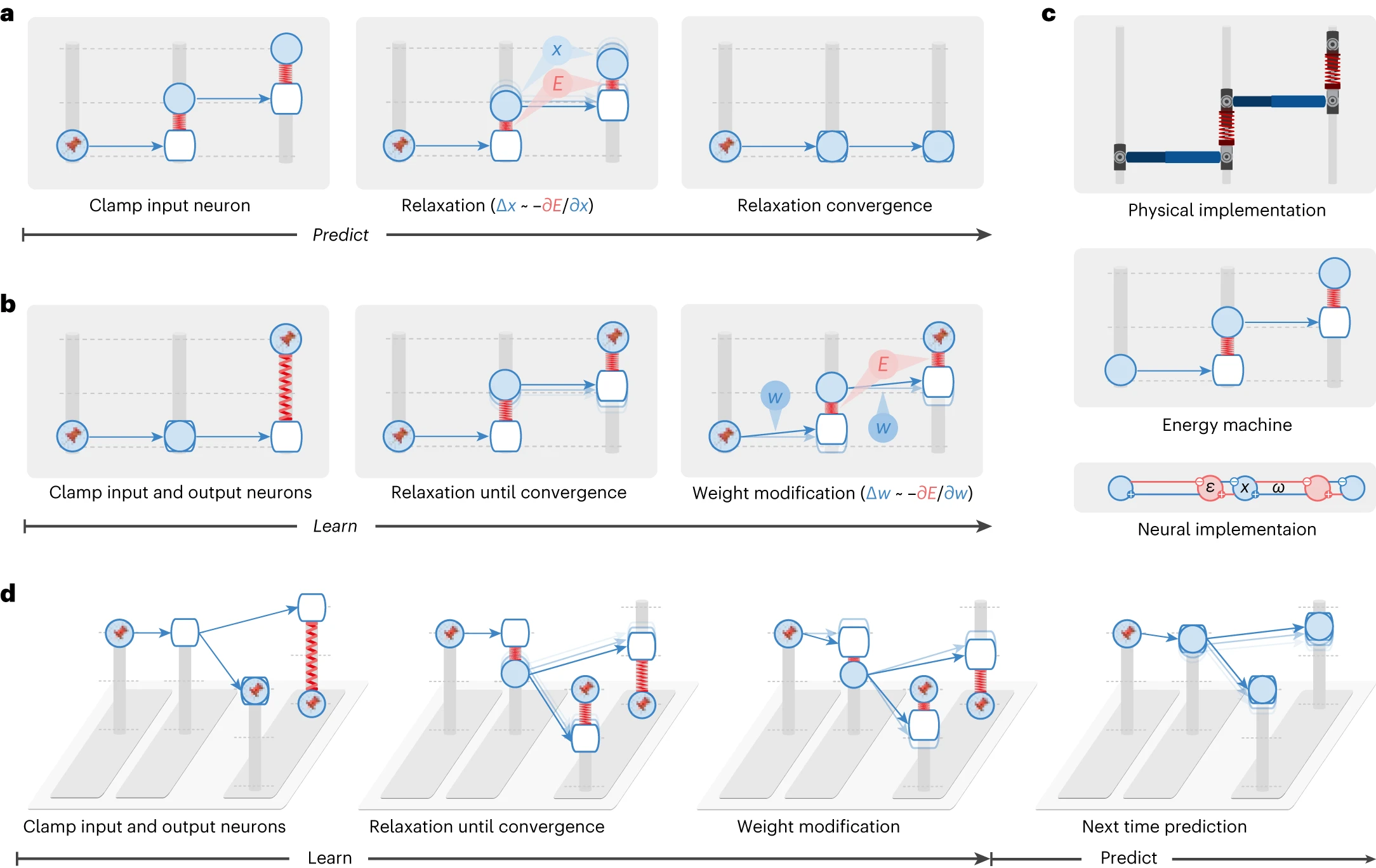
図2 | エネルギー機械は、エネルギーベースのネットワーク、展望的構成のメカニズム、およびその理論的な利点に関する新しい理解を明らかにします。

エネルギーベースのネットワークのサブセットは、同等の計算を実行する機械的な機械として視覚化できます。ここでは、予測符号化ネットワーク[^12],[^18]に対応するエネルギー機械を示します。エネルギー機械では、ニューロンの活動は支柱上をスライドするノード（塗りつぶされた円で表される）の高さに対応します。ニューロンへの入力は、同じ支柱上の空白のノードで表されます。シナプス接続は、塗りつぶされたノードから空白のノードを指すロッドに対応します。荷重は、シナプス後ニューロンへの入力がシナプス前ニューロンの活動にどのように依存するかを決定します。したがって、ロッドの角度に影響を与えます。エネルギーベースのネットワークでは、緩和（つまり、ニューラルダイナミクス）と荷重修正（つまり、荷重ダイナミクス）はどちらもエネルギーを最小化することによって駆動され、これはそれぞれノードを移動してロッドを調整することによるエネルギー機械の緩和に対応します。a,b, エネルギー機械によって視覚化されたエネルギーベースのネットワークでの予測（a）と学習（b）。ピンは、神経活動が入力またはターゲットパターンに固定されていることを示します。ここでは、緩和が展望的な神経活動を推論し、荷重がその方向に向かって修正されるメカニズム（展望的構成と呼ぶ）であることが明らかになります。c, 予測符号化ネットワーク[^12],[^18]の物理的な実装（上）と接続性（下）。このネットワークのダイナミクスは、中央のエネルギー機械のダイナミクスと数学的に等価です（詳細については、方法を参照）。d, 図1の学習問題をエネルギー機械で視覚化したもの。展望的構成のメカニズムのおかげで、正しい出力に干渉することなく、不正解の出力を改善するように学習します。
エネルギー関数を最小化することによって駆動されるエネルギーベースのネットワークのダイナミクスは、スプリング上の合計弾性ポテンシャルエネルギーを削減することによって駆動されるエネルギー機械の緩和にマップされます。エネルギーベースのネットワークによる予測には、入力ニューロンを提供された刺激に固定し、他のニューロンの活動を更新することが含まれます。これは、エネルギー機械の片側を固定し、ノードを移動させてエネルギー機械を緩和させることに対応します（図2a）。エネルギーベースのネットワークによる学習には、入力ニューロンと出力ニューロンを対応する刺激に固定し、最初に残りのニューロンの活動を収束させ、次に荷重を更新することが含まれます。これは、エネルギー機械の両側を固定し、最初にノードを移動させてエネルギー機械を緩和させ、次にロッドを調整することに対応します（図2b）。
エネルギー機械は、エネルギーベースのネットワークの本質を明らかにします。荷重修正前の緩和により、ネットワークは、荷重の修正によってエラーが修正された後に発生するはずの神経活動に対応する新しい神経活動の構成、つまり展望的な活動に落ち着きます（したがって、このメカニズムを展望的構成と呼びます）。例えば、図2bの2層目の「ニューロン」はその活動を増加させますが、この活動の増加は、その後の荷重修正（最初のニューロンと2番目のニューロンの間の接続）によっても引き起こされます。簡単に言うと、エネルギーベースのネットワークの緩和は、学習後の展望的な神経活動を推論し、荷重はその方向に向かって修正されます。これにより、荷重修正が先行し、神経活動の変化がその結果として続くバックプロパゲーションとは区別されます。
図2cの下部には、予測符号化ネットワーク[^12],[^18]の接続性が示されています。このネットワークのダイナミクスは、上に示したエネルギー機械のダイナミクスと数学的に等価です。予測符号化ネットワークには、支柱のノードに対応するニューロン（青）と、スプリングに対応する予測エラーをエンコードする個別のニューロン（赤）が含まれます。詳細については、方法と補足図1を参照してください。ここでは、予測符号化ネットワークを記述する方程式をリストし、それらがニューラル実装と提案されたエネルギー機械にどのようにマップされるかを示します。
エネルギー機械を使用して、図2dは図1からの学習問題をシミュレートします。ここでは、展望的構成が実際に緩和を通じて学習の結果とその副作用を予見できることがわかります。したがって、1回の反復で副作用を修正します。そうでない場合、バックプロパゲーションには複数回の反復が必要です。

 見込み構成の利点：干渉の低減と高速学習ここでは、上記のシナリオにおける干渉を定量化し、干渉の低減がパフォーマンスの向上にどのようにつながるかを示します。本文のすべてのシミュレーションでは、見込み構成は予測符号化ネットワークに実装されています（他のエネルギーベースモデルは補足ノートのセクション2.1で検討されています）。また、予測符号化ネットワークのパフォーマンスを、バックプロパゲーションでトレーニングされた人工ニューラルネットワーク（ANN）と比較します。これは、それらが密接に関連しているため、比較が公平になります。特に、予測符号化ネットワークには再帰的な接続が含まれていますが、荷重が対応する値に設定されている場合、標準的なフィードフォワードANNと同じ予測を入力に対して生成します（入力が制約されているが出力が制約されていない場合、図2a）[^12],[^14]。したがって、損失は両方のモデルで荷重の同じ関数であるため、予測符号化ネットワークでの勾配降下による損失の直接的な最小化（これは自然なトレーニング方法ではありません）は、ANNでのバックプロパゲーションと同じ荷重の変化を生成します。したがって、予測符号化ネットワークとバックプロパゲーションを比較することで、学習アルゴリズムの効果（見込み構成とバックプロパゲーションのような損失の直接的な最小化）を分離できます。
図3aでは、図1の例における出力ニューロンの活動を、バックプロパゲーションと見込み構成の間で比較します。最初は両方の出力ニューロンがアクティブであり（右上）、出力はニューロンの1つが非アクティブになるターゲットに向かって変化する必要があります（赤いベクトル）。見込み構成による学習は、バックプロパゲーションの場合（紫色の点線ベクトル）よりもターゲットとより良く整合する出力の変化（紫色の実線ベクトル）をもたらします。
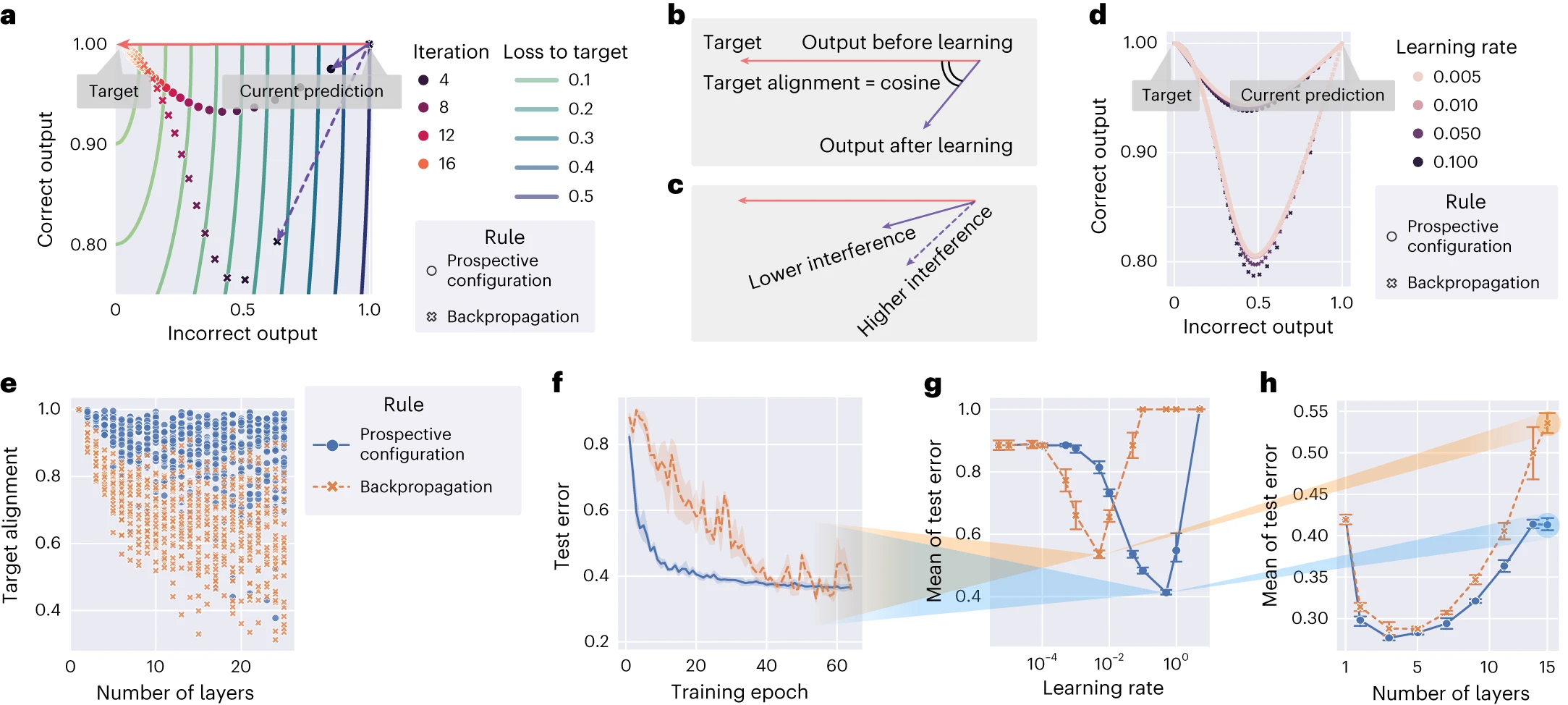
図3 | 見込み構成による学習は、ターゲットに沿った方向に、出力ニューロンの活動を変化させます。

a、図1のネットワークのシミュレーション。両方の学習規則でトレーニングされた「反復」中の、正しい出力ニューロンと正しくない出力ニューロンの変化を示しています。ここでは、見込み構成による学習（紫色の実線ベクトル）は、バックプロパゲーションによる学習（紫色の破線ベクトル）よりもターゲット（赤いベクトル）とより良く整合しています。b、「ターゲットアライメント」によって干渉を定量化できます。これは、ターゲットの方向（赤いベクトル）と学習の方向（紫色のベクトル）のコサイン類似度です。c、ターゲットアライメントが高いほど干渉が少なく、その逆も同様です。d、aと同じ実験を、0.005から0.5の範囲の学習率で繰り返しました。マーカーのサイズで表され、学習率の選択は両方の方法の軌跡をわずかに変化させますが、結論は学習率に関係なく保持されることが示されています。e、ネットワークの深さの関数として、両方の学習規則でトレーニングされたランダムに生成されたネットワークのターゲットアライメント。各記号は、単一のランダムに生成されたパターンでトレーニングした結果のターゲットアライメントを示しています。f、15層の深層ニューラルネットワークを使用した両方の学習規則について、異なるカテゴリに属する衣服の画像を含むFashionMNIST[^60]データセットでのトレーニング中のテストエラー。ここで、「テストエラー」とは、テストセットのすべてのサンプルの中で誤って分類されたサンプルの比率を指します。g、学習率の関数として、トレーニングエポックにわたるテストエラーの平均（テストエラーがどれだけ速く低下するかを反映）。fとhの結果は、gの対応する曲線の最小値を与える学習率に対するものです。h、他のネットワークの深さのテストエラーの平均。各ポイントは、ネットワークの深さの対応する設定で、各学習規則に対して独立して最適化された学習率からのものです。

e〜hでは、構造が深くなるにつれて、見込み構成が著しい利点を示しています。f〜hの各実験は、n = 3のランダムシードで繰り返されました。エラーバーとバンドは、68％の信頼区間を表しています。
最初の荷重更新後、ネットワークがターゲットを正しく予測できるようになるまで、複数の反復をシミュレートします。ここで、「反復」とは、エージェントが刺激を提示され、その刺激のために1回の荷重更新を行うたびに発生することを指します。バックプロパゲーションからの出力は複数回の反復後にターゲットに到達できますが、「正しいニューロン」の出力は学習中にターゲットから逸脱し、その後戻ってきます。これは、ネットワークが学習プロセスのどの時点でも「テスト」できる生物学的学習では特に望ましくない効果です。これは、生存の可能性に影響を与える誤った決定につながる可能性があるためです。対照的に、見込み構成は、この効果を大幅に軽減します。
バックプロパゲーションは荷重の空間でコストを直接削減するために荷重を修正しますが（つまり、勾配降下を実行します）、驚くべきことに、そしてむしろ破壊的に、結果として得られる出力活動をターゲットに直接押し進めません。これを説明するために、図3aは等高線でコストを視覚化しています。コストの勾配に従って出力ニューロンの活動を変更することは、等高線に対して直交する変化、つまり赤い矢印で示される変化に対応します。ただし、バックプロパゲーションは、破線の矢印で示される異なる方向に​​出力を変更します。他の荷重の更新の影響を考慮せずに、荷重を独立して最適化すると、異なる層への異なる荷重の更新が互いに干渉するため、出力活動がターゲットに向かって直接更新されません。対照的に、見込み構成は、最初にニューラル活動の望ましい構成を見つけることによって、他の荷重を更新した結果を考慮します。このようなメカニズムはバックプロパゲーションにはありませんが、エネルギーベースネットワークでは自然です。補足図2は、これらの2つのモデルが学習中に荷重空間と出力空間でどのように進化するかを直接比較したものです。干渉は、ターゲットの方向（現在の出力からターゲットまで）と学習の方向（現在の出力から学習後の出力まで、両方ともターゲットなしで測定）の間の角度によって定量化できます。この角度のコサインとして「ターゲットアライメント」を定義します（図3b）。したがって、高い干渉は低いターゲットアライメントに対応します（図3c）。
ターゲットアライメントは学習率の影響をほとんど受けないことを強調することは役立ちます（図3d）。これは、学習率が出力ニューロンが取る方向と軌跡にほとんど影響を与えないことを示しています。図3aに示されているターゲットアライメントの違いは、より深く、より大きな（ランダムに生成された）ネットワークにも存在します（図3e）。ネットワークに隠れ層がない場合、ターゲットアライメントは1に等しくなります（補足ノート、セクション2.4.1）。ネットワークが深くなるにつれて、バックプロパゲーションのターゲットアライメントは低下します。これは、1つの層の荷重の変化が他の層の変化を妨げ（図1）、バックプロパゲートされたエラーが隠れ層での荷重の適切な修正につながらないためです（補足図2）。バックプロパゲーションは損失を減らす方向に荷重を修正するため、小さい学習率では正のターゲットアライメントを持ちますが、必ずしも1に近いとは限りません。対照的に、見込み構成は、その過程ではるかに高い値を維持します。見込み構成のこの高いターゲットアライメントは、次のように理論的に説明できます。（1）見込み構成とターゲット伝播と呼ばれるアルゴリズムの間には密接な関係があります[^26]（補足図3および補足ノート、セクション2.2に示されています）、（2）特定の条件下では、ターゲット伝播[^26]は1のターゲットアライメントを持ちます（参考文献27;補足図4および補足ノート、セクション2.4.2に示されています）。したがって、ターゲット伝播との関係は、見込み構成がより高いターゲットアライメントを持つ理由について、理論的な洞察（数値検証付き）を提供します。
より高いターゲットアライメントは、学習の効率に直接つながります。15層の深層ニューラルネットワークを使用した視覚分類タスクでのトレーニング中のテストエラーは、バックプロパゲーションよりも見込み構成の方が速く減少します（図3f）。
ここに示されているデータ全体を通して、学習率がプロットに表示されていない場合、プロットはグリッド検索を介して設定の下で各ルールに対して独立して最適化された最適な学習率に対応します。最適化ターゲットは、学習パフォーマンスまたは実験データとの類似性のいずれかです（詳細は各実験の方法に記載されています）。したがって、たとえば、図3fは、トレーニングの進行状況としてのテストエラーを示しており、学習率は各学習規則に対して独立して最適化されています。最適化ターゲットは、トレーニング中の「テストエラーの平均」であり、トレーニング中にテストエラーがどれだけ速く減少するかを反映しています。図3gは、両方の学習規則について、異なる学習率に対するこのテストエラーの平均をプロットしており、曲線の最小値を与える学習率が図3fで使用されました。図3hは、他の深さのネットワークで実験を繰り返し、ネットワークの深さの関数として、トレーニング中のテストエラーの平均を示しています。これらのネットワークはタスクを学習できないため、平均エラーは深さが低いほど高くなり、より深いネットワークのトレーニングには時間がかかるため、深さが大きいほど高くなります。重要なことに、バックプロパゲーションと見込み構成の間のギャップは、より深いネットワークで広がり、ターゲットアライメントの違いと並行しています。より深いネットワークでの効率的なトレーニングは、霊長類の視覚皮質[^28]など、深いことが知られている生物学的ニューラルシステムにとって重要です。
補足ノートのセクション2.3では、見込み構成の正式な理論を展開し、その利点に関するさらなる図と分析を提供します。補足図5は、見込み構成を正式に定義し、それが実際に異なるエネルギーベースネットワークで一般的に観察されることを示しています。補足図6および7は、理論から予想される利点を経験的に検証および一般化し、見込み構成がより正確なエラー割り当てと、それぞれより少ない気まぐれな荷重修正をもたらすことを示しています。

 見込み構成の利点：生物学的に関連するシナリオでの効果的な学習これらの利点に触発されて、見込み構成が、生物学的システムが直面するさまざまな学習問題を、バックプロパゲーションよりも実際にはうまく処理することを示します。機械学習の分野では、学習パフォーマンスをテストするための効果的なベンチマークが開発されているため、自然環境での学習と主要な機能を共有する古典的な機械学習問題のバリアントを使用します。そのような問題には、各経験の後に荷重を更新する必要があるオンライン学習（トレーニング例のバッチではなく）[^29]、複数のタスクでの継続的な学習[^30]、変化する環境での学習[^31]、限られた数のトレーニング例での学習、および強化学習[^4]が含まれます。前述のすべての学習問題において、見込み構成はバックプロパゲーションよりも著しい優位性を示しています。
まず、図1の例に基づいて、見込み構成はバックプロパゲーションよりも学習に必要なエピソードが少ないと予想されます。比較を行う前に、バックプロパゲーションを使用してANNをトレーニングする方法について説明します。通常、荷重は、個々の例から導出された更新の平均に基づいて、トレーニング例のバッチの後にのみ変更されます（図4a）。実際、バックプロパゲーションは、トレーニングを安定させる必要があるため[^33]、人間のレベルのパフォーマンスに到達するために複数の経験にわたる平均化に大きく依存しています[^32]。対照的に、生物学的システムは各経験の後に荷重を更新する必要があり、そのような設定での学習パフォーマンスを比較します。サンプリング効率は、トレーニング中のテストエラーの平均によって定量化できます。これは、バッチサイズ（更新が平均化される経験の数）の関数として図4bに示されています。効率は、バックプロパゲーションではバッチサイズに強く依存します。これは、気まぐれな荷重更新を平均化するためにバッチトレーニングが必要であるためです。一方、見込み構成では、荷重の変化が本質的に気まぐれではなく、バッチ平均化の必要性が低いため、この依存性は弱くなります（補足図7）。重要なことに、見込み構成は、生物学的設定のように、より小さなバッチサイズでより速く学習します。さらに、最終的なパフォーマンスは、テストエラーの最小値によって定量化できます。これは、バッチサイズが1に等しい場合にトレーニングされたときに図4cに示されています。ここでは、見込み構成はバックプロパゲーションよりも著しい優位性を示しています。
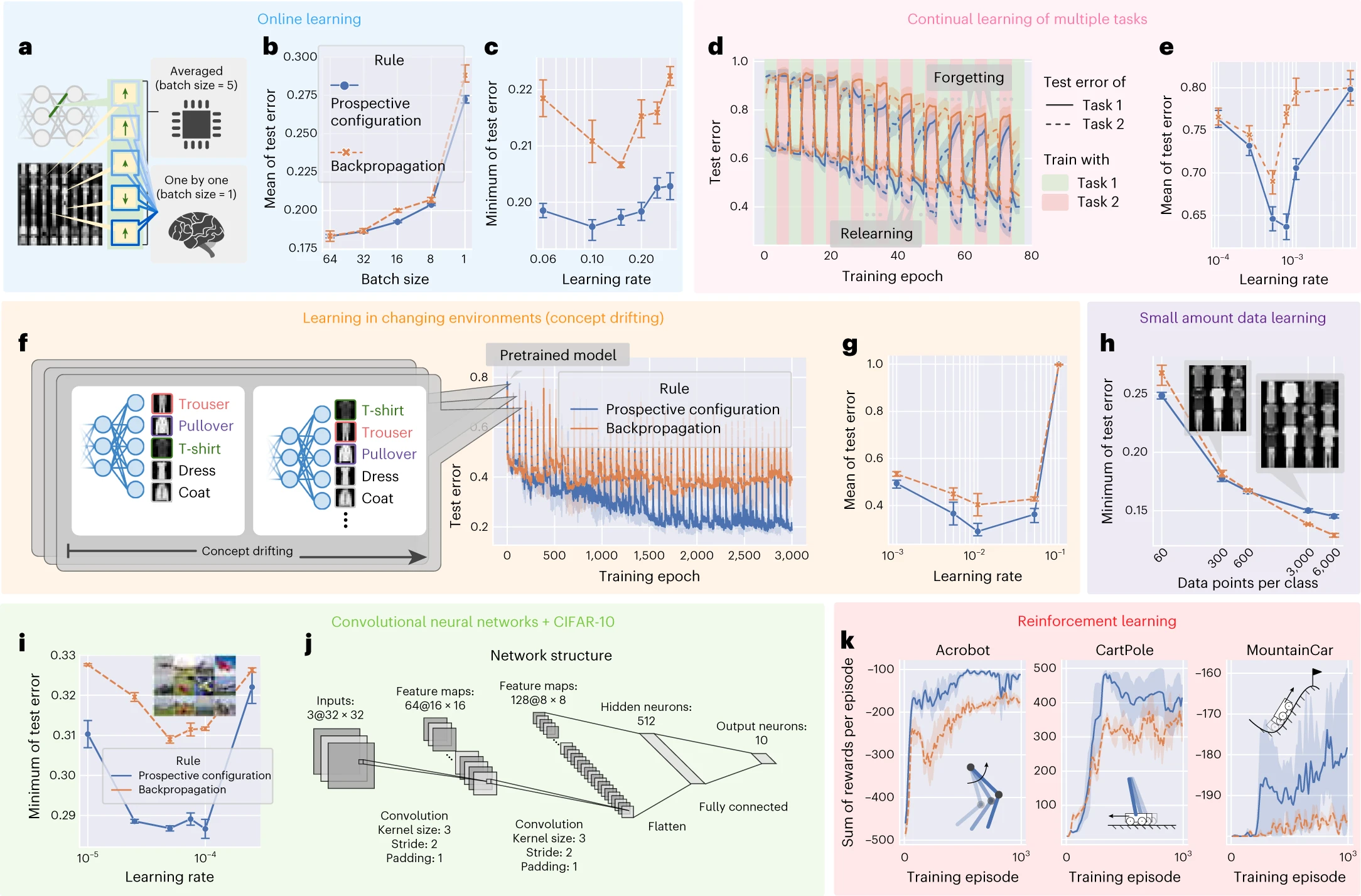
図4 | 見込み構成は、生物学的システムが直面するさまざまな学習状況において、バックプロパゲーションよりも優れたパフォーマンスを実現します。

a〜k、学習状況には、オンライン学習[^29]（a〜c）、複数のタスクの継続的な学習[^30]（d〜e）、変化する環境での学習[^31]（f〜g）、限られた量のトレーニング例での学習（h）、および強化学習[^4]（k）が含まれます。各状況に対応するグラフは、同じ背景色でグループ化されています。各状況のシミュレーションは、メソッドで説明されている「デフォルト設定」とは、このタスクに固有の単一の側面が異なります。たとえば、デフォルト設定にはミニバッチでのトレーニングが含まれているため、オンライン学習を調査するためにa〜cでのみバッチサイズが1に設定されましたが、残りのグループではより大きなデフォルト値に設定されました。教師あり学習の設定では、完全に接続されたネットワーク（a〜h）はFashionMNIST[^60]データセットで評価され、畳み込みニューラルネットワーク[^35]（iおよびj）はCIFAR-10（参考文献36）データセットで評価されました。強化学習の設定（k）では、完全に接続されたネットワークが3つの古典的な制御問題で評価されました。学習率が表示されていない場合、プロット内の各ポイント（実験の設定）は、その設定で各ルールに対して独立して最適化された最適な学習率に対応します。a、個々の例に対する荷重修正を平均して「統計的に優れた」値を取得できるコンピュータと、別の計算を行う前に1つの修正を適用する必要がある生物学的システムとの間のトレーニング設定の違い。b、バッチサイズの関数としてのトレーニング中のテストエラーの平均。c、学習率の関数としてのトレーニング中のテストエラーの最小値。d、2つのタスクの継続的な学習中のテストエラー。e、学習率の関数としてのトレーニング中の両方のタスクのテストエラーの平均。f、概念ドリフトで学習する場合のトレーニング中のテストエラー。g、学習率の関数としての概念ドリフトでのトレーニング中のテストエラーの平均。h、異なる量のトレーニング例（クラスごとのデータポイント）でのトレーニング中のテストエラーの最小値。i、CIFAR-10（参考文献36）データセットで、見込み構成とバックプロパゲーションでトレーニングされた畳み込みニューラルネットワークのトレーニング中のテストエラーの最小値。j、iで使用される畳み込みニューラルネットワークの構造の詳細。k、3つの古典的な強化学習タスク（インセット）でのトレーニング中のエピソードごとの報酬の合計。エピソードは、環境の初期化から終了状態に到達するまでの期間です。a〜hの各実験は、n = 10のランダムシードで繰り返されました。i〜kの各実験は、これらの実験はより高価であるため、n = 3のランダムシードで繰り返されました。エラーバーとバンドは、68％の信頼区間を表しています。
第二に、生物学的有機体は複数のタスクを順番に学習する必要がありますが、ANNは破滅的な忘却を示します。新しいタスクでトレーニングすると、以前に学習したタスクのパフォーマンスが大幅に低下します[^16],[^34]。図4dのデータは、2つのタスクで交互にトレーニングした場合のパフォーマンスを示しています（タスク1はFashionMNISTデータセットでランダムに選択された5つのクラスを分類し、タスク2は残りの5つのクラスを分類します）。見込み構成は、以前のタスクの忘却を回避し、現在のタスクを再学習するという点で、バックプロパゲーションよりも優れています。結果は図4eにまとめられています。
第三に、生物学的システムは、変化する環境に迅速に適応する必要があることがよくあります。これをシミュレートする一般的な方法は「概念ドリフト」[^31]です。ここでは、出力ニューロンからセマンティックな意味へのマッピングの一部が定期的にシャッフルされます。トレーニング反復の特定の回数が経過するたびにシャッフルされます（図4f）。概念ドリフトを使用したトレーニング中のテストエラーを図4fに示します。エポック0の前に、両方の学習規則は同じ事前トレーニング済みモデル（バックプロパゲーションでトレーニング済み）で初期化されます。したがって、エポック0は、モデルが概念ドリフトを初めて経験する時間です。結果は図4gにまとめられており、このタスクでは、平均エラーに特に大きな違いがあることを示しています（最適な学習率の場合）。見込み構成のこの大きな利点は、どの荷重を修正するかを最適に検出できること（補足図6）、および変更に適応しながら既存の知識を保持できること（図1）に関連しています。他の情報を更新しながら重要な情報を維持するこの能力は、変化する可能性のある自然環境での生存にとって重要であり、見込み構成はこの点で非常に大きな利点があります。
さらに、生物学的学習は、利用可能なデータが限られていることも特徴としています。モデルがより少ない例でトレーニングされた場合、見込み構成はバックプロパゲーションよりも優れています（図4h）。
見込み構成の利点がより大きなネットワークや問題にもスケールアップすることを示すために、両方の学習規則でトレーニングされたCIFAR-10（参考文献36）で畳み込みニューラルネットワーク[^35]を評価しました（図4i）。ここでは、見込み構成がバックプロパゲーションよりも著しい利点を示しました。畳み込みネットワークの詳細な構造を図4jに示します。
生物学的システムにとってのもう1つの重要な課題は、どのアクションを実行するかを決定することです。強化学習理論（たとえば、Q学習）は、さまざまな状況でさまざまなアクションから得られる予想される報酬を学習することで解決されることを提案しています[^37]。そのような報酬の予測は、ニューラルネットワーク[^4]によって行うことができ、見込み構成またはバックプロパゲーションでトレーニングできます。3つの古典的な強化学習タスクでのトレーニング中のエピソードごとの報酬の合計を図4kに示します。ここでは、見込み構成がバックプロパゲーションよりも著しい利点を示しています。この大きな利点は、強化学習がネットワーク荷重の気まぐれな変化に特に敏感である可能性があるためです（ターゲット出力は、ネットワーク自体が新しい状態に対して予測した報酬に依存するため、方法）。
見込み構成の優れた学習パフォーマンスに基づいて、この学習メカニズムは進化によって支持されてきたと予想されます。したがって、次のセクションでは、バックプロパゲーションよりも学習中のニューラル活動と行動をより良く説明できるかどうかを調査します。

 見込み構成の証拠：学習中の潜在状態の推論見込み構成は、学習の前に、脳が最初にフィードバックから環境の潜在状態を推論することを提案する理論に関連しています[^38],[^39],[^40]。ここでは、この推論は、見込み構成を介してニューラル回路で実現できると提案します。ここでは、フィードバックの後、「隠れ層」のニューロンがこの潜在状態をエンコードする見込み活動パターンに収束します。潜在状態の推論を含むさまざまな以前の研究からのデータは、見込み構成によって説明できることを示します。これらのデータは、以前はベイズモデル[^38],[^39]などの複雑で抽象的なメカニズムによって説明されていましたが、ここでは、そのような推論が見込み構成によってタスクの重要な要素のみをエンコードする最小ネットワークによってどのように実行できるかをメカニズム的に示します。
フィードバックからの潜在状態の動的な推論は、感覚運動学習中に行われることが最近提案されています[^39]。この実験では、参加者はさまざまな文脈でさまざまな運動外乱を受け、これらの外乱を補償することを学習しました。行動データは、フィードバックを受けた後、参加者が最初にフィードバックを使用して文脈を推論し、次に推論された文脈の力を適応させたことを示唆しています。見込み構成はこれらの行動データを再現できますが、バックプロパゲーションはできません。
具体的には、タスク（図5a）では、参加者は外乱を経験しながら、開始点からターゲット点までスティックを移動するように求められました。参加者は、トレーニング、ウォッシュアウト、およびテストを含む、一連のトライアルブロックを経験しました（図5c〜e）。トレーニングセッション中、外乱の異なる方向、正（+）または負（–）が、それぞれ青（B）または赤（R）の背景の異なる文脈で適用されました。これらのトライアルをB+およびR–と表記します。これらのトライアルは、潜在状態に関連付けられている可能性があります。これを[B]および[R]と表記します。たとえば、潜在状態[B]は、背景Bと外乱+の両方に関連付けられている可能性があります。タスクの次の段階は、背景Bが表示されていなくても、潜在状態[B]が外乱+によってアクティブ化できるかどうかを調査するように設計されました。したがって、参加者はR+（つまり、外乱+ですが、背景Bはありません）を含むさまざまなトライアルを経験しました。具体的には、ウォッシュアウトセッション（外乱が提供されない）の後、テストセッションでは、参加者は4つの可能なテストトライアルのいずれかを経験しました：B +、R +、B–、およびR–。テストトライアルでの学習を評価するために、青い背景の2つのトライアルで、テストトライアルの前後の運動適応（つまり、最終的なスティックの位置とターゲットの位置の差）を測定しました（図5e）。これらの2つのトライアル間の適応の変化は、テストトライアルで発生した青い文脈に関する学習の反映です。参加者がフィードバックを背景色（B）のみに関連付けた場合、適応の変化はテストトライアルB+およびB–でのみ発生します。ただし、実験データ（図5f）は、R+トライアルでもかなりの適応変化があったことを示しています（B–トライアルよりもさらに大きかった）。
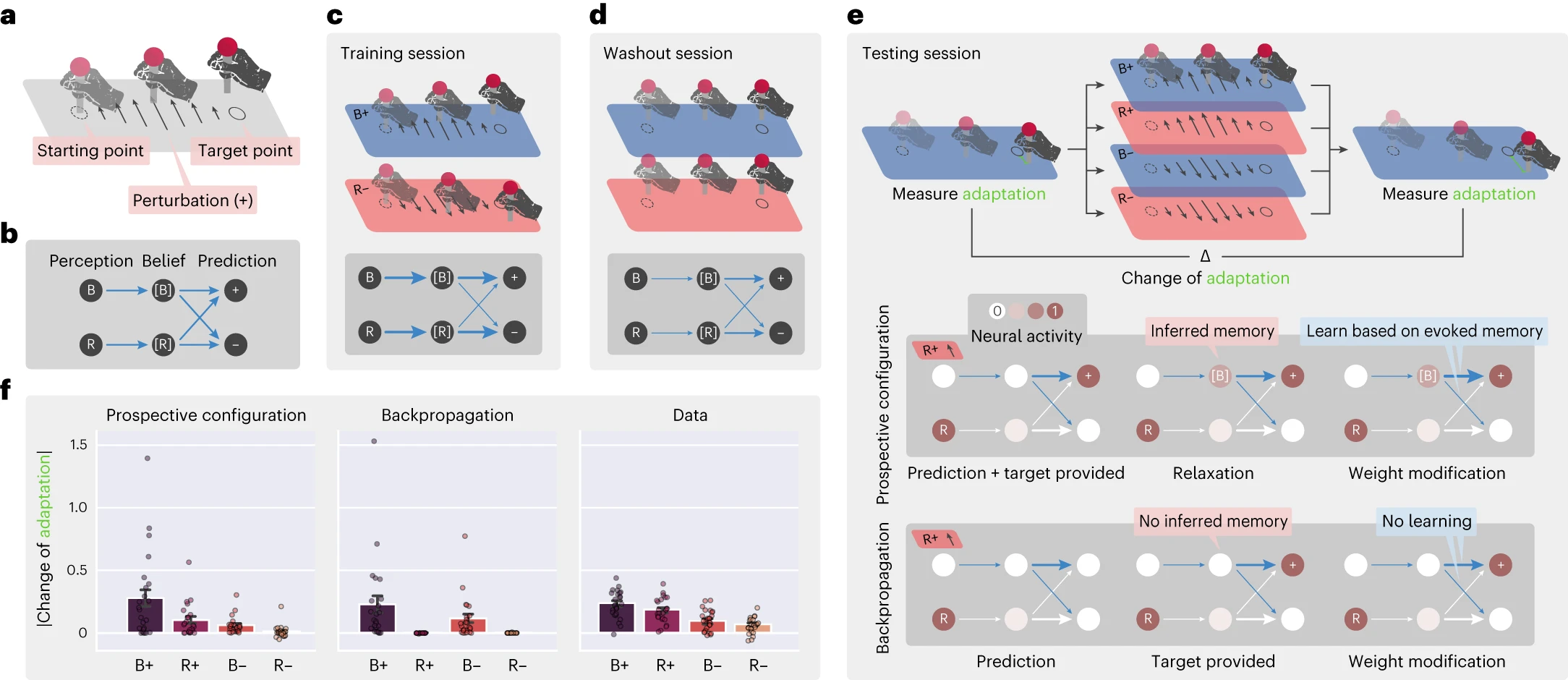
図5 | 見込み構成は、人間の感覚運動学習における文脈推論を説明します。a、参加者が外乱を経験しながら、開始点からターゲット点までスティックを移動するように求められた実験トライアルの構造。

b、タスクの最小ネットワーク。背景（BおよびR）から文脈の信念（[B]および[R]）への関連付け、および文脈の信念から外乱の予測（+および–）への関連付けをエンコードする6つの接続が含まれます。c〜e、トレーニング（c）、ウォッシュアウト（d）、およびテスト（e）を含む、参加者が経験したセッションのシーケンス。濃い灰色のボックスは、セッション後の予想されるネットワークを示しており、太さは接続の強度を表しています。テストセッションでは、濃い色のボックスは、2つの学習規則がR+トライアルでどのように異なる方法で学習するかを説明しており、fの違いにつながります。f、人間の参加者から測定された行動データと比較した2つの学習規則の予測。見込み構成はデータの主要なパターンを再現しますが、バックプロパゲーションはそうではありません。行動実験には24人の参加者がいたため、各実験はn = 24のランダムシードで繰り返されました。
このタスクでの学習をモデル化するために、入力ノードが背景色をエンコードし、出力が2つの方向の運動補償をエンコードするニューラルネットワークを検討しました（図5b）。重要なことに、このネットワークには、2つの背景（[B]および[R]）に関連付けられた文脈にいるという信念をエンコードする隠れニューロンも含まれています。ランダムに初期化された荷重から、実験[^39]の正確な手順でトレーニングされた、この最小ネットワークを使用した見込み構成は、行動データを再現できますが、バックプロパゲーションはできません（図5f）。
見込み構成は、R+テストトライアルで適応の変化を生み出すことができます。これは、+フィードバックの後、トレーニング中にこのフィードバックに関連付けられていた文脈[B]もアクティブ化し、この潜在状態の補償を学習できるためです。この推論がモデルでどのように行われるかを明らかにするために、図5c、dの概略図は、セッション中のネットワークの荷重の進化を示しています（太さは接続の強度を表しています）。図5eの概略図は、R+への曝露後の2つの学習規則の違いを示しています。Bは認識されていませんが、見込み構成は、青い文脈[B]から+への正の接続がトレーニングセッション中に構築されたため、青い文脈[B]の信念の適度な励起を推論します。[B]の活動により、[B]から+および–への荷重の学習が可能になりますが、バックプロパゲーションは[B]から発生する荷重を変更しません。
説明を簡単にするために、最小ネットワークを使用したシミュレーションを提示しました。ただし、補足図8は、一般的な完全に接続された構造とより多くの隠れニューロンを持つネットワークが、見込み構成を使用する場合は上記のデータを複製できますが、バックプロパゲーションを使用する場合は複製できないことを示しています。
動物の条件付けの研究では、複数の刺激を含む学習タスクでのフィードバックが、提示されていない刺激に関する学習を引き起こす可能性があることも観察されています[^41],[^42]。1つの例を補足図9に示します。ここでは、見込み構成で説明できますが、バックプロパゲーションでは説明できないことを示しています。

 見込み構成の証拠：学習中のタスク構造の発見見込み構成は、強化学習の基礎となるタスク構造も発見できます。具体的には、異なるオプションの報酬確率が独立していないタスクを検討します[^38]。この研究では、参加者は2つのオプションから選択していました。報酬確率は、一方のオプションが他方よりも高い報酬確率を持つように制約されていました（図6a）。報酬確率が交換されることがあり、一方の確率が増加すると、他方の確率が同じ量だけ減少しました。注目すべきことに、記録された機能的磁気共鳴画像法（fMRI）データは、参加者が2つのオプションの値が負の相関関係にあることを学習し、各トライアルで両方のオプションの値の推定値を反対の方法で更新したことを示唆しました。この結論は、報酬の期待値をエンコードする内側前頭前皮質（mPFC）からの信号の分析から導き出されました。図6cに示されているデータは、2つの連続するトライアルで選択を行った後のこの信号を比較しています。報酬を受け取らなかったトライアル（「罰トライアル」）とその次のトライアルです。参加者が両方のトライアルで同じオプションを選択した場合（「ステイ」）、信号が減少し、参加者が期待する報酬が減少したことを示しています。注目すべきことに、参加者が次のトライアルで他のオプションを選択した場合（「スイッチ」）、信号が増加し、一方のオプションに対する負のフィードバックが他方のオプションの値の推定値を増加させたことを示唆しています。そのような学習は、標準的な強化学習モデルでは予測されていません[^38]。
図6 | 見込み構成は、強化学習中に基礎となるタスク構造を発見できます。

a、強化学習タスク。人間の参加者は、異なる確率で報酬（コインを獲得）または罰（コインを失う）につながる2つのオプションから選択する必要がありました。報酬の確率は、2つのオプション間で時々逆転しました。b、タスクの重要な要素をエンコードする最小ネットワーク。c、見込み構成およびバックプロパゲーションでトレーニングされたネットワークからの、選択されたオプションに対応する出力ニューロンの活動。人間の参加者で測定されたfMRIデータ（つまり、mPFCのピーク血中酸素レベル依存（%BOLD）信号）と比較されます。見込み構成は、罰トライアル後の次の選択が他のオプションに切り替える場合、期待値（mPFCの%BOLD信号でエンコード）が増加するという重要な発見を再現します。トライアルの数は元の論文に記載されていないため、両方の学習規則についてn = 128トライアルをシミュレートしました。エラーバーは、68％の信頼区間を表しています。
このタスクは、どちらのオプションが優れているかをエンコードする潜在状態を持ち、この潜在状態が両方のオプションの報酬確率を決定するものとして概念化できます。したがって、タスクにいることをエンコードする入力ニューロン（シミュレーションでは1に等しい）、潜在状態をエンコードする隠れニューロン、および2つのオプションの報酬確率をエンコードする2つの出力ニューロンを含む、この構造を反映するニューラルネットワークを検討します（図6b）。ランダムに初期化された荷重から、実験[^38]の正確な手順でトレーニングされた、この最小ネットワークを使用した見込み構成は、データを再現できますが、バックプロパゲーションはできません（図6c）。補足図10では、見込み構成がフィードバックに基づいて隠れニューロンの活動を更新することで、報酬のある選択を推論できるため、これらのデータを再現することを示しています。
まとめると、提示されたシミュレーションは、見込み構成が、多様なタスクで驚くべき学習効果の範囲を説明できる一般的な原理であることを示しています。
「Discussion」に続きます。

https://zenn.dev/tanegoma/articles/7a2aa92f627168