この記事は「倒立振子ロボットを現代制御で動かしたい」シリーズの一本です。
- モデル化(この記事)
- 直立制御
- 遠隔操作
はじめに
以前、Atom Matrixを使って倒立振子ロボットを製作しました。しかし立てることはできたものの、安定性や応答性といった点はまだまだ先人たちの作品には及びませんでした。
そこで今回は新しく設計したハードウェアを使い、直立だけでなくスムーズな前後進も可能なロボットを作ることを目標とします。
新しいハードウェアではDCモータに替えてステッピングモータを使用します。
そこで、回転数(角速度)を定量的に決められるというステッピングモータの特徴を生かし、現代制御理論によりロボットの姿勢(角度)と前後進(速度)を同時に制御することを目指します。
この記事ではまずプロジェクトの第1段階として、現代制御理論で必要となる倒立振子ロボットのモデルを導出します。
モデリングの方法は下記の記事を参考にしました。
ただし今回はステッピングモータを使用するため少し違ったモデルになっています。
運動方程式の導出
まずはロボットの運動方程式を求めます。
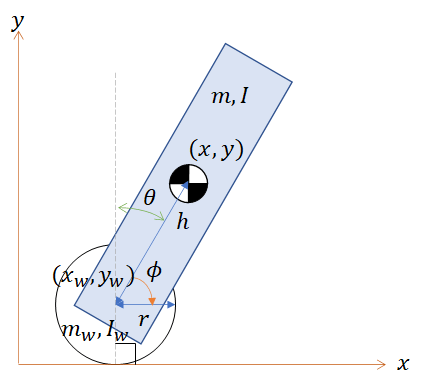
まず、ロボットの仕様は下記の通りとします。
- 車体は質量m、重心周りの慣性モーメントIの剛体
- 車輪は半径r、質量m_w、重心周りの慣性モーメントI_wの剛体
- 車軸から車体の重心までの距離h
- 車輪は地面に対して滑らないものとする
また、下記の変数を導入します。
- 世界に対する車体の角度\theta
- 車体に対する車輪の角度\phi
- 重心の位置(x,y)
- 車軸の位置(x_w, y_w)
運動方程式の導出にはラグランジュ力学を使用します。
そのためには運動エネルギーTとポテンシャルエネルギーUを求める必要がありますが、まずは運動エネルギーから求めていきます。
まずは車輪部分の速度(\dot{x_w},\dot{y_w})から求めます。
まず世界に対する車輪の角度は\theta + \phiなので角速度は\dot{\theta} + \dot{\phi}となり、さらに滑らないと仮定しているので
\begin{align}
\dot{x_w}=r(\dot{\theta}+\dot{\phi})
\end{align}
です。
また明らかにy_w=rなので
\begin{align}
\dot{y_w}=0
\end{align}
です。
次に、車体の重心の速度(\dot{x},\dot{y})を求めます。車輪と重心の位置関係を組み合わせると、
\begin{align}
x &= x_w + h \sin\theta \\
y &= y_w + h \cos\theta
\end{align}
より
\begin{align}
\dot{x} &= r(\dot{\theta}+\dot{\phi}) + h \dot{\theta} \cos\theta \\
\dot{y} &= -h \dot{\theta} \sin\theta
\end{align}
です。
以上より並進運動のエネルギーは
\begin{align}
\begin{split}
&\frac{1}{2} m (\dot{x}^2+\dot{y}^2) + \frac{1}{2} m_w (\dot{x_w}^2+\dot{y_w}^2)\\
= &\frac{m \left(h^{2} \dot{\theta}^{2} + 2 h r \cos{\left(\theta \right)} \dot{\phi} \dot{\theta} + 2 h r \cos{\left(\theta \right)} \dot{\theta}^{2} + r^{2} \dot{\phi}^{2} + 2 r^{2} \dot{\phi} \dot{\theta} + r^{2} \dot{\theta}^{2}\right)}{2} \\
&+ \frac{m_{w} r^{2} \left(\dot{\phi} + \dot{\theta}\right)^{2}}{2}
\end{split}
\end{align}
となります。
また、回転運動のエネルギーは車体と車輪の(世界に対する)角速度を使って
\begin{align}
\frac{1}{2} I \dot{\theta}^2 + \frac{1}{2} I_w (\dot{\theta}+\dot{\phi})^2
\end{align}
と表せるので、両者を合わせた運動エネルギーは
\begin{align}
\begin{split}
T = &\frac{I \dot{\theta}^{2}}{2} + \frac{I_{w} \left(\dot{\phi} + \dot{\theta}\right)^{2}}{2} \\
&+ \frac{m \left(h^{2} \dot{\theta}^{2} + 2 h r \cos{\left(\theta \right)} \dot{\phi} \dot{\theta} + 2 h r \cos{\left(\theta \right)} \dot{\theta}^{2} + r^{2} \dot{\phi}^{2} + 2 r^{2} \dot{\phi} \dot{\theta} + r^{2} \dot{\theta}^{2}\right)}{2} \\
&+ \frac{m_{w} r^{2} \left(\dot{\phi} + \dot{\theta}\right)^{2}}{2}
\end{split}
\end{align}
となります。
次にポテンシャルエネルギーを求めますが、車体に働く重力だけを考えればよいので単純に
\begin{align}
U = mgy = mg(r + h\cos\theta)
\end{align}
です。
これをラグランジュ方程式を使って解きます。
今回はステッピングモータを使用しており、車体に対する車輪の角度\phi(=モータの角度)は自由に設定できるので、一般化座標は\thetaのみです。
また非保存力などもないので、ラグランジュ方程式はシンプルに
\begin{align}
\frac{d}{dt} \frac{\partial L}{\partial \dot{\theta}} - \frac{\partial L}{\partial \theta} = 0 \\
\end{align}
となります(ただしL=T-U)。
この式を整理すると
\begin{align}
\begin{split}
&\frac{d}{dt} \frac{\partial L}{\partial \dot{\theta}} - \frac{\partial L}{\partial \theta} \\
= & - g h m \sin{\left(\theta \right)} - h m r \sin{\left(\theta \right)} \dot{\theta}^{2} + \left(I_{w} + h m r \cos{\left(\theta \right)} + m r^{2} + m_{w} r^{2}\right) \ddot{\phi} \\
& + \left(I + I_{w} + h^{2} m + 2 h m r \cos{\left(\theta \right)} + m r^{2} + m_{w} r^{2}\right) \ddot{\theta} \\
= & 0
\end{split}
\end{align}
となります。
この(12)式がこのロボットの運動方程式です。
状態空間モデル
運動方程式は求まりましたがこのままでは非線形なので、ロボットがほぼ直立状態にあると仮定して式を線形化します。
具体的には\sin\theta=\theta, \cos\theta=1, \dot{\theta}^2=0と近似します。
\begin{align}
\begin{split}
&- g h m \theta + \left(I_{w} + h m r + m r^{2} + m_{w} r^{2}\right) \ddot{\phi} \\
&+ \left(I + I_{w} + h^{2} m + 2 h m r + m r^{2} + m_{w} r^{2}\right) \ddot{\theta} \\
= &0
\end{split}
\end{align}
かなりシンプルになりました。
次は制御理論で扱えるように、行列を使った
\begin{align}
\dot{\mathbf{x}} = A \mathbf{x} + B \mathbf{u}
\end{align}
という状態方程式の形に変換します(今回は観測方程式は考えず、状態変数をそのまま計測できるものとしています)。
今回は状態変数を\mathbf{x} = [\theta \ \dot{\theta} \ \dot{\phi}]^T、入力を\mathbf{u} = [\ddot{\phi}]^Tとします。
つまり「ステッピングモータの角加速度を操作することで、車体の角度と角速度および車輪の角速度が変化する」というモデルになります。
(13)式を\ddot{\theta}=\ldotsの形に変形し、さらに\dot{\theta},\dot{\phi}についての式を追加すると、このロボットの状態方程式は次のようになります。
\begin{align}
\underbrace{\begin{bmatrix}
\dot{\theta} \\ \ddot{\theta} \\ \ddot{\phi}
\end{bmatrix}}_{\dot{\mathbf{x}}}
=
\underbrace{\begin{bmatrix}
0 & 1 & 0 \\
a & 0 & 0 \\
0 & 0 & 0
\end{bmatrix}}_{A}
\underbrace{\begin{bmatrix}
\theta \\ \dot{\theta} \\ \dot{\phi}
\end{bmatrix}}_{\mathbf{x}}
+
\underbrace{\begin{bmatrix}
0 \\ b \\ 1
\end{bmatrix}}_{B}
\underbrace{\ddot{\phi}}_{\mathbf{u}}
\end{align}
ただし
\begin{align}
a = \frac{g h m}{I + I_{w} + h^{2} m + 2 h m r + m r^{2} + m_{w} r^{2}} \\
b = \frac{- I_{w} - h m r - m r^{2} - m_{w} r^{2}}{I + I_{w} + h^{2} m + 2 h m r + m r^{2} + m_{w} r^{2}}
\end{align}
です。
具体的な値を求める
上で求めた式に実際のロボットのパラメータを代入していきます。
ですが慣性モーメントなどは計測が難しいので、今回は部品のデータシートなどの公開情報や推測をもとにFusion 360でモデリングして値を算出しました(プロパティの物理情報を使用)。

パラメータは下記の通りでした(変な単位ですがこれはFusion 360に合わせたためです)。
- 車体の質量m = 181.731\ \mathrm{g}、慣性モーメントI = 61096.991\ \mathrm{g\ mm^2}
- 車輪の半径r = 60\ \mathrm{mm}、質量m_w = 21.994\ \mathrm{g}、慣性モーメントI_w = 13319.524\ \mathrm{g\ mm^2}
- 車軸から車体重心までの距離h = 14.924\ \mathrm{mm}(実際は左右非対称なため約4mm左にずれているが無視)
- (重力加速度g = 9800\ \mathrm{mm/s^2})
これらのパラメータを(16),(17)に代入するとa = 22.6443895687399,\ b = -0.774824387837912となったため、状態方程式の係数部分は
\begin{align}
A &= \begin{bmatrix}
0 & 1 & 0 \\
22.6443895687399 & 0 & 0 \\
0 & 0 & 0
\end{bmatrix} \\
B &= \begin{bmatrix}
0 \\ -0.774824387837912 \\ 1
\end{bmatrix}
\end{align}
と求まりました。
可制御性の判定
このシステムの可制御性を求めると、
\begin{align}
\mathrm{rank} M = \mathrm{rank} \left[ B \ A B \ A^2 B \right] = 3
\end{align}
であったので、(外乱を考えなければ)適切な入力を与えれば立たせられる見込みがあるといえます。
まとめ
この記事では、ステッピングモータを使った倒立振子ロボットの運動方程式を導出し、状態空間モデルに変形した上で、具体的なパラメータを代入して可制御性の判定を行いました。
次回は今回求めた式をもとに制御器を求め、実際にロボットの制御に挑戦します。
果たしてロボットは立つのでしょうか・・・



Discussion