特異値分解(SVD)による画像の低ランク近似
はじめに
Eckart-Youngの定理により、dランクの行列分解において特異値分解(SVD)は元の行列とのフロベニウスノルムを最小にする点で、最良の近似行列を得ることができます。この記事ではランクを変数に取り特異値分解をすることでフロベニウスノルムの変化がどうなるか、また分解元の行列を画像とした場合において、ランクごとにどのように画像が復元されるかを確認します。
実装
実装について
GoogleColabで実験しました。スニペット中のprompt: というコメントはColabの機能でコード生成に用いたプロンプトを指しています。実験の都合上、生成されたコードを一部改変していたり、そもそも同じプロンプトでも同一のコードを出力する保証はないと思うのでご了承ください。
imageioというライブラリを使います。サンプル画像としてライブラリ側で用意しているコーヒーの画像(coffee.png)を利用します。
import numpy as np
import imageio.v3 as iio
import matplotlib.pyplot as plt
A = iio.imread('imageio:coffee.png', mode='L')
print(A.shape)
(400, 600)
サイズが400*600の画像です。
rank = np.linalg.matrix_rank(A)
print(rank)
400
画像を行列とみなしたとき、行列のランクは400でした。自然な画像であれば、基本的にはランクはmin(縦の画素数, 横の画素数)と一致するはずですので、想定通りです。
# prompt: plot image
plt.imshow(A, cmap='gray')
plt.show()
# prompt: 特異値分解
U, s, Vh = np.linalg.svd(A, full_matrices=False)
print(U.shape, s.shape, Vh.shape)
(400, 400) (400,) (400, 600)
さて、特異値分解の結果が得られたのでフロベニウスノルムの変化を確認します。グラフでは元画像のスケール（0-255）と比較しやすいように正規化しています。
# prompt: rankを1刻みで増やして誤差（フロベニウスノルムを画素数の平方根で割った値）を計算し、折れ線グラフをプロット
import numpy as np
import imageio.v3 as iio
import matplotlib.pyplot as plt
# Load the image
A = iio.imread('imageio:coffee.png', mode='L')
# Calculate the Frobenius norm of the original image
frobenius_norm = np.linalg.norm(A, 'fro')
# Create a list of ranks to try
ranks = range(1, A.shape[0] + 1)
# Calculate the error for each rank
errors = []
for rank in ranks:
# Truncate the singular values and matrices
s_trunc = s[:rank]
U_trunc = U[:, :rank]
Vh_trunc = Vh[:rank, :]
# Reconstruct the image
A_approx = np.dot(U_trunc, np.dot(np.diag(s_trunc), Vh_trunc))
# Calculate the error
error = np.linalg.norm(A - A_approx, 'fro') / np.sqrt(A.size)
errors.append(error)
# Plot the error vs. rank
plt.plot(ranks, errors)
plt.xlabel('Rank')
plt.ylabel('Error')
plt.title('Error vs. Rank')
plt.show()
誤差が単調減少していることがわかります。ランク400付近の値を確認してみます。
errors[-5:]
[0.08284203766427897,
0.06950368212998516,
0.05426237984006046,
0.03705074199673772,
3.564445877579145e-13]
最終的にはほぼ0になっており、数値計算の誤差を無視すれば完全に復元できていることがわかります。
余談ですが、誤差の差分の数列（階差数列）を考えると、階差数列は概ね減少傾向にありますが単調減少とはなっていないようです。（最後の方で値が上がったり、グラフからは読み取りにくいですが前半でも途中で跳ねる瞬間があります。）
# prompt: ランクを1増やすことでどれだけerrorが減るかをプロット
# Calculate the error difference for each rank
error_diffs = [errors[i] - errors[i+1] for i in range(len(errors) - 1)]
# Plot the error difference vs. rank
plt.plot(ranks[1:], np.log1p(error_diffs))
plt.xlabel('Rank')
plt.ylabel('Error Difference')
plt.title('Error Difference vs. Rank')
plt.show()
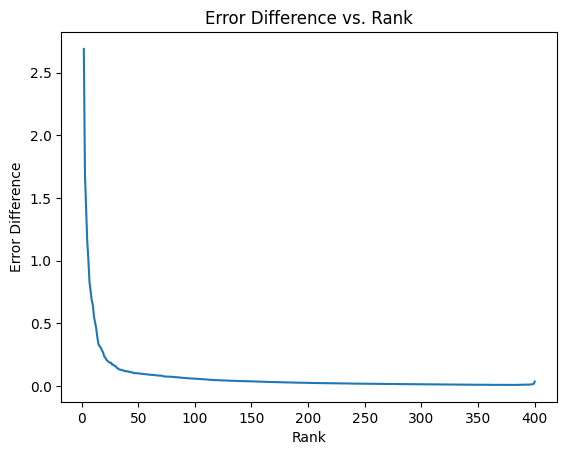
次に画像の復元を考えます。ランクを増やすごとに、画像が良く復元できていく様子を定性的に確認できます。
# prompt: [1, 2, 3, 5, 10, 30, 100, 200, 400]で画像を復元する
# Create a list of ranks to try
ranks = [1, 2, 3, 5, 10, 30, 100, 200, 400]
# Reconstruct the image for each rank
for rank in ranks:
# Truncate the singular values and matrices
s_trunc = s[:rank]
U_trunc = U[:, :rank]
Vh_trunc = Vh[:rank, :]
# Reconstruct the image
A_approx = np.dot(U_trunc, np.dot(np.diag(s_trunc), Vh_trunc))
# Plot the reconstructed image
plt.imshow(A_approx, cmap='gray')
plt.title(f'Rank: {rank}')
plt.show()
参考文献
- SVDによる画像の低ランク近似
- Eckart-Youngの定理
- 推薦システム: 統計的機械学習の理論と実践
-
推薦システム―マトリクス分解の多彩なすがた―
- 証明も記載されています
Discussion