変分推論MPCのための事前分布の学習 (1): FlowMPPI
本記事は名古屋大学の本田康平(https://kohonda.github.io/ )による寄稿です。
はじめに
ロボットの制御や運動計画で人気を博しているモデル予測制御 (MPC) ですが,MPCの中でもサンプルベースMPCは手頃に実装できる上に,性能もそこそこ良いため非常に使い勝手が良いです.サンプルベースMPCとは,制御入力のサンプルを複数用意して,それらを制御対象の予測モデルを用いて未来の状態を予測・評価して,最適な制御入力をするというものです.(例えば,Dynamic Window Approach (DWA)もその一種です.) これらは予測モデルやコスト関数が微分不可能であったり非線形性が強い場合でも利用できるので,とても使い勝手が良く,モデルベース強化学習などでもしばしば利用されます.
近年,サンプルベースMPCに対して確率推論的にアプローチをすることでサンプル効率の向上やモデルの不確実性を考慮しようという研究が盛んに行われています.例えば,Model Predictive Path Integral Control (MPPI) もその一つで,とてもポピュラーな手法になりつつあります.このような確率推論的なMPCは何らかの事前確率分布からサンプリングを基に最適解を推論をするため,この事前分布の形状が性能に大きく影響します.
本記事では,確率推論MPCにおけるサンプリング分布を学習によって獲得する手法であるVariational Inference MPC using Normalizing Flows and Out-of-Distribution Projection (通称FlowMPPI) (Robotics: Science and Systems (RSS), 2022)について紹介します.
【準備】 変分推論 MPC; Variational Inference MPC (VI-MPC)
FlowMPPIについて紹介する前に,事前知識として確率推論型MPCの代表手法の一つであるVariational Inference MPC (VI-MPC)について簡単に紹介します.VI-MPCはUC BerkeleyのSergey Levineが提唱した,Control as Inferenceと呼ばれる,MPCや強化学習を最適制御問題を確率推論として再定義するアプローチを源流とします.以下では,変分推論 (Variational Inference) を用いてMPCを解く概要を簡単に説明します.
初めに変数を定義します.T時刻先までの未来の予測状態系列をX= [ x_0, x_1, \dots, x_T ],入力系列をU= [u_0, u_1, \dots, u_{T-1} ]とします.ここで,x_0は現在の状態であり,x_tは予測時刻tにおける状態です.また,u_tは時刻tにおける制御入力です.XとUを合わせて,軌跡\tau:= (X, U)とします.また,軌跡\tauに対して何らかのコスト関数コスト関数をJ(\tau)が与えられ,状態遷移モデルp(x_{t+1} \mid x_t, u_t)が予測モデルとして与えられているとします.
VI-MPCでは,最適性条件を満たす軌跡\tauの事後確率p(\tau \mid o=1)を求めることを目的とします.ここで,oは"最適性"を示すバイナリ変数で,o=1の時に最適性条件を満たすとします.ただし,p(o\mid \tau)は予め設計したコスト関数J(\tau)によって,
p(o \mid \tau) \simeq \exp \left( - J(\tau) \right)
として評価することが一般的です.最終的に,求めたp(\tau \mid o=1)を用いてサンプリングや重みつき平均などを取ることで,最適軌跡\tau (すなわち,最適な制御入力系列U) を決定します.
今,求めたい事後確率p(\tau \mid o=1)の形状は複雑なので一般的に求めることは難しいです.そこでVI-MPCは,p(\tau \mid o=1)の代わりに,p(\tau \mid o=1)とのKLダイバージェンスを最小化するような分布q(\tau)を制御入力系列の事前分布q(U)を用いて求めます.すなわち,
\begin{align}
q^*(\tau) &= \arg \min_{q(\tau)} \mathbb{KL} \left[ q(\tau) || p(\tau \mid o=1) \right] \nonumber \\
& (\dots \text{ベイズの定理を用いた式変形}) \nonumber \\
& \simeq \arg \min_{q(\tau)} \mathbb{E}_{q(\tau)} \left[ - \log p(o \mid \tau) \right] - \mathcal{H} \left(q(U) \right) \nonumber \\
& \simeq \arg \min_{q(\tau)} \underbrace{\mathbb{E}_{q(\tau)} \left[ J(\tau) \right] - \mathcal{H} \left(q(U) \right)}_{\mathcal{L}_{\rm{VI-MPC}}} \tag{1}
\end{align}
となり,p(\tau \mid o=1)の近似表現,q(\tau)は適当な事前分布q(U)を仮定することで求めることができます.式 (1)の第一項は,コスト関数J(\tau)の期待値を最小化する項であり,第二項は,事前分布q(U)のエントロピーであり,一種の正規化項となります.VI-MPCでは,式 (1) を鏡像勾配降下法によって解くことでq(\tau)を求めています.また,q(U)をガウス分布と仮定することでMPPIの更新式と等価な式が導出されます.詳しい式展開はこちらの論文が参考になります.
ここで話を戻しますと,FlowMPPIの立場としては,式 (1) の事前分布q(U)をガウス分布や混合ガウス分布などの"適当な"分布を用いるのではなく,環境に特化させた複雑な事前分布q(U | C) (Cはcontext vector) を学習によって獲得することで,性能を向上させることを目指します.
FlowMPPI = VI-MPC x VAE x Normalizing Flow
モチベーション: 環境に特化した事前分布q(U | C)の獲得
前述した式 (1) の変分推論MPCを解くためには,何らかの事前分布q(U)を仮定し,そこから入力系列をサンプリングする必要があります.例えば,MPPIでは前回の最適解の系列を平均としたガウス分布を事前分布として用います.基本的に変分推論MPCはこのサンプルの"質"が良ければとても良いサンプル効率や制御性能を発揮することが知られています.逆に,生成されたサンプルの質が悪いと制御性能が著しく低下します.例えば,ロボットの衝突回避であれば,できるだけ衝突しない (=質の良い) サンプルをサンプリングするような事前分布を用いることが望ましいということになります.つまり,ロボットの動作する環境を事前分布に組み込んで,その環境に応じた事前分布を獲得することによって変分推論MPCの性能の向上が期待できます.
手法の概要
FlowMPPIは移動ロボットやマニピュレータなどへの適用を想定し,一組のスタート・ゴールおよび,外界観測情報としてSinged Distance Field (SDF) を環境として仮定します.この3つの情報で指定された動作環境に応じた事前分布を学習によって獲得する手法です.ただし,教師データとして必要なものはスタート・ゴール・SDFのみでGround Truthなどは必要ありません.
下図にFlowMPPIの全体像を示します.FlowMPPIはスタート・ゴール・SDFを入力として,サンプルUを生成します.具体的にはA,B,Cの3つのモジュールに大きく分かれています.以下ではそれぞれを説明していきます.
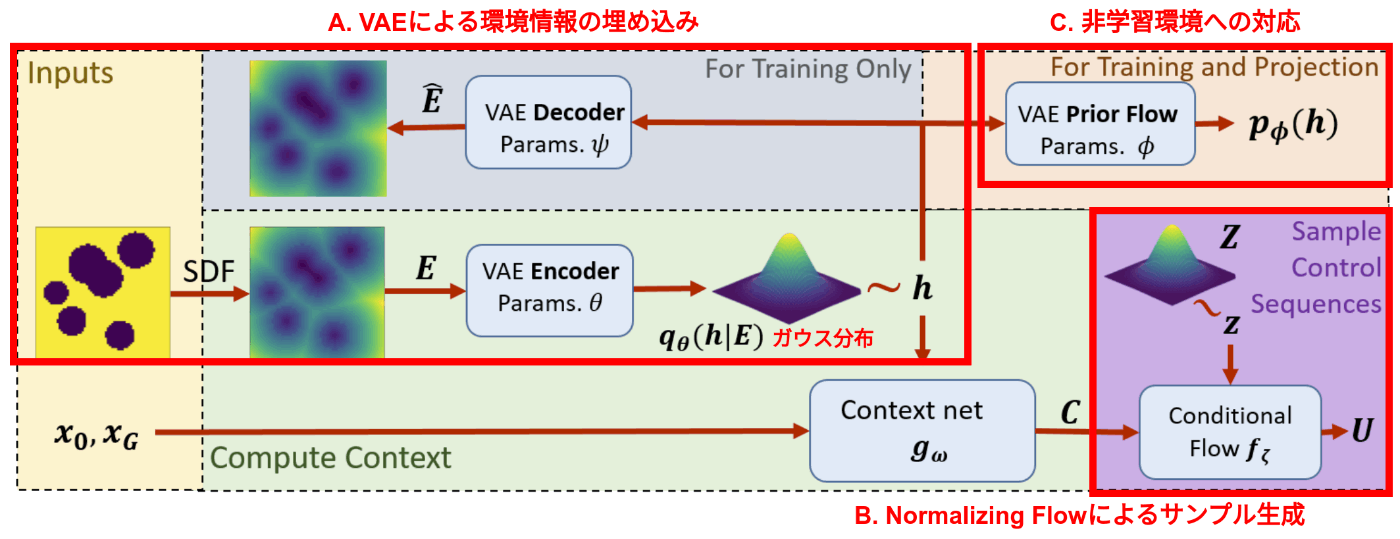
A. VAEによる環境情報の埋め込み
まず,SDFとして表現されている観測情報を利用するために,Variational Auto Encoder (VAE) によってSDFを低次元ベクトルhとして圧縮表現します.ここでは,まず入力データであるSDF EをEncoderによって潜在空間に落とし込みます.その潜在空間においてガウス分布からベクトルhをサンプリングします.そして,Decoderによってそのベクトルhから入力データ (すなわちSDF) を生成するように学習します.結果として,VAEによって環境の観測情報SDFを低次元ベクトルh \sim q_{\theta}(h \mid E)として表現することができます.
なお,損失関数は通常のVAEと同様に以下のようになります.
\begin{align}
& \mathcal{L}_{\rm{VAE}} = \mathbb{E}_{q_{\theta}(h \mid E)} \left[ - \log p_{\psi}(E|h) \right] + \mathbb{KL} \left[ q_{\theta}(h \mid E) || p_{\phi}(h) \right] \tag{2}
\end{align}
第一項は,潜在変数hから入力SDF Eを生成する確率 (尤度) を最大化する項 (再構成誤差項) であり,第二項は,潜在変数hが分布p_{\phi}(h)に近づくようにする正則化項です.p_{\phi}(h)は通常のVAEでは定数の平均と分散によるガウス分布 (例えば\mathcal{N}(0, I)) ですが,FlowMPPIではVLEという手法に則ってガウス分布のパラメータ\phiも同時に学習します.ただし,p_{\phi}(h)は後ほど再登場しますが,FlowMPPIを理解する上ではp_{\phi}(h) = \mathcal{N}(0, I)としておいても問題ありません.
B. Normalizing Flowによる事前分布q(U|C)の獲得
Aで得られたSDFを表現するベクトルhは上概要図のcontext netに入力され,スタート・ゴール情報と統合されて,Context vector C=g_w(h, x_{\rm{start}}, x_{\rm{goal}})として出力されます.つまり,Cは観測情報+スタート+ゴールを表します.
FlowMPPIは,このcontext vector Cを入力として,サンプルUを生成するための事前分布q(U \mid C)をNormalizing Flowによって表現します.
Normalizing Flowとは,簡単な確率分布から複雑な確率分布を表現するための手法です.具体的には,簡単な確率分布 (例えばガウス分布) から変換を繰り返すことで,複雑な確率分布を表現します.詳細な式展開は省略しますが,要は,データドリブンで近似した非線形変換f_{\zeta}を用いて,U \sim f_{\zeta}(z, C)とすることでサンプリングを行います.ここで,z \sim p(z)は簡単な確率分布 (例えばガウス分布) からサンプリングしたノイズです.
Normalizing Flowは生成モデルの一種ですが,特徴の一つとしてその尤度の計算が比較的容易であることが挙げられます.その尤度p(U|C)は
\begin{align}
& p(U|C) = p(z)\left|\det \frac{\partial f^{-1}_{\zeta}(z, C)}{\partial z}\right| \tag{3}
\end{align}
と表現されます.
さて,通常のNormalizing flowであれば,非線形変換f_{\zeta}を学習するために教師データを入力として上記の (対数) 尤度を最大化していきますが,FlowMPPIでは代わりに,式 (1) のVI-MPCの損失関数\mathcal{L}_ {\rm{VI-MPC}}を最小化するように学習します.つまり,式 (3) から式 (1) の\mathcal{H}(q(U))を計算し,\mathcal{L}_ {\rm{VI-MPC}}を最小化することでNormalizing Flowのパラメータ\zetaを学習します.なお,詳細は割愛しますが,鏡像勾配降下法によって,\mathcal{L}_ {\rm{VI-MPC}} の勾配はUの重み付き平均に置き換えられるため,コスト関数や予測モデルの微分情報が利用できない場合でも学習が可能です.
以上より,上述したVAEのパラメータ\theta, \phi,context netのパラメータw,Normalizing Flowのパラメータ\zetaは全てまとめて,以下の単一損失関数を最小化することで同時に学習されます.
\begin{align}
\mathcal{L}_{\rm{FlowMPPI}} &= \mathcal{L}_{\rm{VAE}} + \mathcal{L}_{\rm{VI-MPC}} \nonumber
\end{align}
C. Projectionによる非訓練環境への対応
ここまで説明したFlowMPPIはVAEとNormalizing Flowを用いることで,訓練環境におけるVI-MPCの損失関数を小さくするような事前分布を獲得することができます.しかし,実際のロボットの制御では,訓練環境とは異なる非訓練環境で汎化することが求められます.そこで,FlowMPPIではもうひと工夫加えて,訓練環境と異なる環境でも対応できるようにします.(個人的にはここがこの論文の一番面白いパートだと思います.)
アプローチとしては,実際のオンライン制御ループにおいて,
- SDF入力Eがどの程度訓練環境と異なるか (Out-of-Distribution (OOD) score) を推定する
- OOD scoreを小さくするようにVAEの潜在変数hをin-distribution方向に補正 (projection) する
- 補正した潜在変数\hat{h}を用いてNormalizing flowによるサンプリングを行う
という手順を踏みます.その結果,Normalizing flowにおいて非訓練環境を訓練環境として幻覚 (hallucinate) させ,信頼度の高いサンプルを生成することができると論文では述べられています.
上記のアプローチにおいてOOD score (=訓練環境との距離) をいかに見積もるかがポイントとなります.SDF Eに対する対数尤度を計算することでこれは見積もることが可能ですが,実際の制御ではUを何千とサンプルするため,その都度SDF Eに対する対数尤度を計算することは非常に計算コストが高いです.そこでFlowMPPIでは代わりに,式 (2) で登場したVAEの潜在変数 hに対する事前分布p_{\phi}(h)の対数尤度をOOD scoreとして利用します.すなわち,OOD scoreは,
\begin{align}
& h \sim q_{\theta}(h \mid E) \nonumber \\
& \mathcal{L}_{\rm{OOD}}(h) = -\log p_{\phi}(h) \nonumber
\end{align}
として計算します.この狙いとしては,式 (2)の第二項において,q_{\theta}(h \mid E)はp_{\phi}(h)に近づくように学習されているため,hがp_{\phi}(h)に近いほど,Eは訓練環境に近いということになります.そこで,hに対する対数尤度をOOD scoreとして利用することで,Eが訓練環境に近いかどうかを大凡見積もることができます.
以上より見積もられたOOD scoreを用いて,潜在変数hをin-distribution方向に投影 (projection) します.具体的には,勾配法を用いて以下のように補正された\hat{h}を計算します.
\begin{align}
& \hat{h} = \arg \min_{h} \left\{\beta \mathcal{L}_{\rm{OOD}}(h) + \mathcal{L}_{\rm{VI-MPC}} \right\} \nonumber \\
\end{align}
ただし,\mathcal{L}_ {\rm{OOD}} (h)のみを最小化してしまうと,\mathcal{L}_ {\rm{VI-MPC}}が大きくなる方向にhが補正されてしまうため,\mathcal{L}_ {\rm{VI-MPC}}との重み付き和を最小化するようにしています.上記の計算によって得られた補正された潜在変数\hat{h}を用いて,Normalizing flowによるサンプリングを行うことによって非訓練環境においても汎化性能を発揮できるようになると報告されています.
実験の様子
NavigationにおけるMPPIとFlowMPPIの比較

※ 上図は動画より引用
上図左のように通常のMPPIでは障害物にスタックしている一方で,FlowMPPIでは障害物を避けてゴールに到達していることがわかります.
実際経験上,MPPIではこの図のように予測ホライズンを長くしてしまうと,ほとんどのサンプルが障害物に衝突してしまい,解が悪化することが多いです.一方,FlowMPPIでは予測ホライズンが長くなっても,衝突せずに解を得ることができるようです.
非訓練環境における"hallucination"の様子

FlowMPPIの特徴的な取り組みとして,非訓練環境においても訓練環境のように"見せかける"ことで汎化性能を向上させるというものがありました.上図は,訓練環境と非訓練実行環境,及び,projectionによって補正した\hat{h}からVAEのdecoderを用いてreconstructionしたSDFが示されています.このSDFを見ると分かるとおり,非訓練環境は実際は長方形の障害物ですが,Normalizing Flowは,これらの長方形障害物を訓練環境のように円盤系の障害物として幻覚していることが確認できます.
まとめ
- FlowMPPIは,環境に特化した事前分布を学習によって獲得することで,VI-MPCのサンプルの質を向上を実現する手法です
- VAEによる環境の表現と,Normalizing Flowによるサンプル生成をVI-MPCに組み込んでいます.
- 環境汎化性能を向上させるために,VAEの潜在変数をprojectionし,非訓練環境においても訓練環境のように"見せかける"ことで汎化性能を向上させています
- なお,後続の研究としてはこちらの論文などがあります



Discussion