📑

制御を失っても安全性を担保する制御法「Passive Safety」

2024/01/18に公開

本記事はスタンフォード大学の田久保勇志（https://www.linkedin.com/in/yuji-takubo/ ）による寄稿です。

はじめに

本記事では、MPC或いはオンラインでの経路設計において重要な、"どのようにして制御の安全性を保証すればよいか"という問題に応答する一つの手法を紹介します。Covariance Steering, MPPI, Stochastic Optimal Control, Markov Decision Processなどの確率的な議論が制御界隈では盛んですが、今回は一味違った安全性について紹介します。

宇宙機のランデブーについて

今回紹介するMPC手法は、かなり特殊/具体的な機体制御のコンテクストから導出されたものです。まずはこのモチベーションを説明します。

まず、(地球の周りをまわる)比較的距離の近い複数の宇宙機の相対的な運動を考えます。特に、機体1 (e.g., 宇宙ステーション, 宇宙ゴミ, 小惑星)に対する機体2 (e.g., 有人宇宙船)の相対的な運動を考慮すると運用上楽なので、慣例的によく用いられています。
ここで重要なのが、(例外的な場所を除いて)宇宙機は相対的に止まることができないということです。ブレーキを踏めば(慣性系に対して)止まってくれる多くの自動車やロボットと異なり、軌道力学に則って一時的に相対速度が0の状態からでも、相対位置/速度がダイナミックに動いていきます。
これは非常に悩ましい問題で、なぜなら接近中の宇宙機に突然の故障が生じてエンジンが作動しなくなった場合(様々な理由で予定した制御入力 $u$ が行えない、というのは比較的ありうるシナリオです)に、『エンジンが再起動しないと、このままではN 秒後に宇宙ステーションに衝突する』というような事故が発生しうるからです。
このような背景から、宇宙機のランデブー/ドッキングではPassive Safety (最悪な制御入力 $u=0$ しか出力できなかったとしても、二つの機体が接触しない)と呼ばれる、特殊な拘束条件が考慮されるようになりました。このようないつ制御対象が制御を失っても、それでも受動的に制約(e.g., 障害物回避)を満たすような制御はハイブリッドシステムによって一般に議論されますが、取り扱いが非常に難しいです。

研究の旨み/革新性

今回紹介する論文は、上記の問題をreachability setを用いることで簡略化＆凸化し、MPCで取り扱えるようにしようというのがモチベーションです。

Passive Safety: 安全性が最重要である制御対象において、制御を失っても確実に制約遵守が行える条件を提示している
”故障からN秒間の範囲で制約を満たす”ような状態の集合は"制約違反領域から-N秒ダイナミクスを伝播させた状態"の集合(Backward Reachable Set, BRS)と補集合の関係があることを示し、これを用いて最適制御の枠組みに落とし込んでいる
BRSは事前に計算が可能なので、これの線形化を各時間で行うことで、凸最適化(二次計画)をベースにしたMPCを作ることができる。

Backward Reachable Set

まず、Backward Reachable Set (BRS) に関して解説します。BRSの導入のモチベーションは、”制御を失ったとしても、その後N秒(ステップ)間は制約を満たし続ける”(今回の例では、宇宙ステーションに制御を失って衝突しない)ような制御を行うことです。

最初に衝突領域 $\mathcal{S}_f$ を定義します。例えば宇宙機2(e.g., 有人宇宙船)が1(e.g.,国際宇宙ステーション)にアプローチを行う際には、宇宙機1を中心としたKeep-out Zone (KOZ)という領域が設定され、この内側に宇宙機2が侵入することを衝突とみなします。
最終的なランデブーの目的は相対位置/速度をゼロにすることですが、数km遠方から接近してくる際には、このような侵入不可領域が定義され、この領域外側ギリギリで相対速度をゼロにしてから最後のドッキング、というのが一般的な運用方法になります。
多くの場合、このKOZは楕円体か直方体(の和集合)で表現されます。

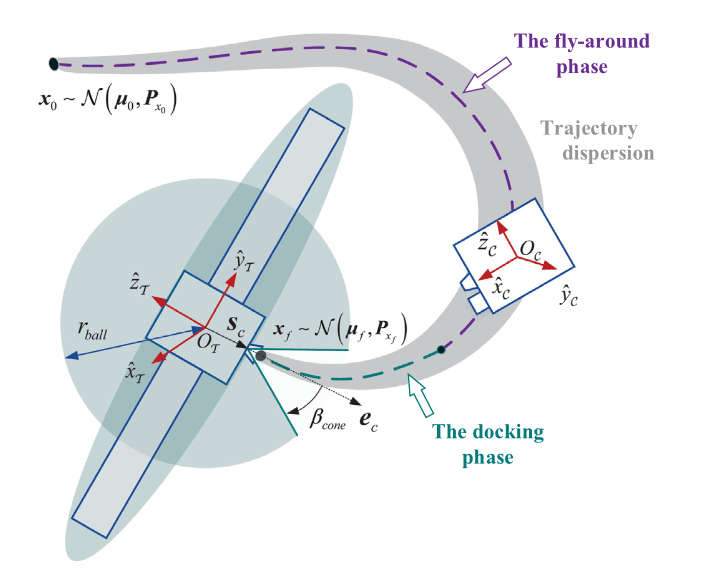
Keep-out zone (KOZ) の参考画像(出典): 青い二つの楕円体がKOZです。この図では楕円体に最終アプローチの錐体の穴が開いていますが、最終アプローチまではこのコーンは埋まっており、完全な楕円体をしています。

さて、この衝突領域 $\mathcal{S}_f$ を最終時刻での状態と見ることで、ここからダイナミクスをマイナス方向に伝播し、Backward Reachable Setを作っていきます。離散時間での線形ダイナミクス

\tag{1} x_{t+1} = f(t,x_t, u_t) = A(t) x_t + B(t) u_t , \quad k \in \mathbb{Z}_{[0,N-1]}

に対して、次のような漸化式でBRSを定義します。

\tag{2} \mathcal{R}_b(t_f; \mathcal{S}_f, t_f) = \mathcal{S}_f, \\ \mathcal{R}_b(t_j; \mathcal{S}_f, t_f) = \{x \in \mathbb{R}^n: f (t_{j-1}, x, 0) \in \mathcal{R}_b(t_j; \mathcal{S}_f, t_f)\},\quad t_j \leq t_f

上の漸化式は、 $t_j$ におけるBRS $\mathcal{R}_b(t_j;\mathcal{S}_f, t_f)$ が、" $t_j$ から $t_f$ まで、 $u=0$ でダイナミクス $f$ を伝播させた時に、 $x(t_f) \in \mathcal{S}_f$ を満たすような $x(t_j)$ の集合" と定義されていることを示しています。

BRSのイメージ。"N-step BRS = (故障の際に)N ステップ後に事故る運命にある状態"です。 $\mathcal{S}_f$ がKOZと同値になります。

参考文献に載せた論文では、これの発展形としてBRS over interval (BRSI)が紹介されています。これはBRSの終端時刻 $t_f$ を動かせるよね、という発想のもと (特に宇宙機は周期的な運動をするので) 軌道一周分の時刻 $t_f = t_k$ に対して得られるBRSの和集合として定義されます。

例: KOZ ( $\mathcal{S}_f$ ) が楕円体であるとき

簡単のために、KOZが原点中心の楕円体

\tag{3} \mathcal{S}_f = \{x:\mathbb{R}^n: x^T P^{-1}x \leq 1\}

で表されると仮定します。例えば、宇宙ステーションにぶつからないようなKOZを組む際には、速度には制約が無く位置のみに楕円体を張りたいので、位置の成分にのみ楕円体が存在するように行列 $P$ を定めます。
ここで、ダイナミクスの線形性と制御 $u=0$ により、任意のN-step BRSは楕円形となり、さらに状態遷移行列 $\Phi$ を用いて、以下のようにあらわすことができます。

\tag{4} \mathcal{R}_b(t_k;\mathcal{S}_f, t_f) = \{x\in \mathbb{R}^n: x^T \Phi(t_f, t_k)^T P^{-1} \Phi(t_f, t_k) x \leq 1 \}

状態遷移行列 $\Phi(t_j, t_j) := \Pi_{i=j}^{h} A(t_i)$ は事前に計算ができ、これがオンラインでのMPCの高速化への布石になります。

BRSの和集合

さて、現実の制御においては重要なのはNステップ後にピッタリ宇宙ステーションにぶつからないようなものではなく、Nステップ以内にぶつからない、ということです。ということで、一つ一つの楕円体ではなく、それの和集合(すなわち"チューブ") $\tilde{\mathcal{R}}$ を考えます。

\tag{5} \tilde{\mathcal{R}}_{[t_f - N, t_f]}(t_f -N; \mathcal{S}_f, t_f) = \bigcup_{t_i = t_f - N}^{t_f} \{x\in\mathbb{R}^n: x^T \Phi(t_f, t_i)^T P^{-1} \Phi(t_f, t_i) x \leq 1 \}

このエリアに侵入した宇宙機が制御を失うとNステップ以内のうちに宇宙ステーションに衝突するので、このエリアに入らないような軌道を作れば、passive safety が達成されます。

この話と全く同様に、原点中心ではない楕円体に対するBRSの和集合も作れたり、直方体に対するBRS(とその和集合)も作ることができます。

二次錐計画を用いたMPCへの適用

ここまで来れば、通常のMPCに上の制約を入れることでPassive-safe MPC を作れます。残念ながらEq. 5が凸ではない(楕円体の集合である)ので、これを線形化(凸化)して凸最適化問題(二次計画)を繰り返し解くことでMPCを作ることを考えます。
今回の例では、各時刻におけるreference state (ひとつ前のステップで解かれた軌道を伝播させたもの) $x_k$ に対して、

原点と機体を結ぶ線上で、機体に最も近い楕円体とその境界上の点を見つける
その点で楕円体に接するような超平面 $h_k^T x_k = 1$ を計算する (=線形化)
MPCの最適制御に、 $h_k^Tx_k\geq1, \forall k = 0,...,Np-1$ の線形不等式を足して最適化する (これが宇宙機と楕円体たちを分離するような線形制約になっています)

を行うことで凸最適化問題を作ります。
(1. で最も近い楕円体が得られたときに、)楕円体に接するような超平面の係数 $h$ は、以下のように計算できます。^[1]

h_k = \frac{2 P^{-1}x_{ref,k}}{\sqrt{x_{ref,k}^T P^{-1}x_{ref,k}}}

ダイナミクスがもともと線形なので典型的なSequential Convex Programmingではないですが、毎ステップで問題を線形化して凸問題を解くという意味では近いアイデアですね。

時刻 $t$ で解かれているMPCのための最適制御問題は、以下のように示されます。予測時間幅は $Np$ としています。
これで得られた解 $U(t) = [u_{0|t}, ..., u_{Np-1|t}]$ のうち、最初の制御 $u_{0|t}$ のみを実行し、次に得られた状態を基に再度凸化を行う、という制御を繰り返していきます。

\begin{align} \text{given} \ & x_{k|t-1}, \ \forall k = 0,...,Np-1 \\ \min_{U(t)} \ & x_{Np|t}^T M x_{Np|t} + \sum_{k=0}^{Np-1} ( x_{k|t}^TQx_{k|t} + u_{k|t}^TRu_{k|t} ) \\ \text{s.t.} \ & x_{k+1|t} = A(t+k) x_{k|t} + B u_{k|t} \\ & x_{0|t} = x(t) \\ & h_{k|t}^Tx_{k|t} \geq 1, \ \forall k=0,\cdots,Np-1 \end{align}

目的関数の第一項はランデブーの終端であるべき状態 $x = \boldsymbol{0}$ に対するペナルティであり、MPCコントローラーがターゲットの宇宙機1に近づいていくことを促します。第二項はLQR制御などで見る、最適制御の基本的な目的関数の形です。
また、given で与えられている $x_{k|t-1}$ は、一つ前の時刻で解かれた最適制御の解を基に得られた軌道になります。このreference trajectoryを基に最後の線形制約の係数 $h_{k|t}$ は計算されています。

宇宙機ランデブー問題への適用例

さて、長くなってしまいましたが、実装結果を見ていきます。
今回も前回の記事同様、地球低軌道を仮定して宇宙機の相対運動を示す2次元空間でのHill-Clohessy-Wiltshireの方程式を使います。

\begin{aligned} & x_{k+1} = Ax_k + B u_k \\ & x = \begin{bmatrix} r_x \\ r_y \\ v_x \\ v_y \end{bmatrix}, \quad u = \begin{bmatrix} \Delta v_y \\ \Delta v_y \end{bmatrix} \\ & A = \begin{bmatrix} 4 - 3\cos(nt) & 0 & \sin(nt)/n & 2(1-\cos(nt))/n \\ 6 (\sin(nt)-nt) & 1 & 2(\cos(nt)-1)/n & (4\sin(nt)-3nt)/n \\ 3n\sin(nt) & 0 & \cos(nt) & 2 \sin(nt) \\ 6n(\cos(nt)-1) & 0 & -2\sin(nt) & 4 \cos(nt) - 3 \end{bmatrix} \\ & B = \begin{bmatrix} 0_{2\times 2} \\ \mathbb{I}_{2\times2} \end{bmatrix} \end{aligned}

また、各種パラメータや条件は以下のようにしました。

\begin{align} N &= 150 \quad (\text{全体のタイムステップ}) \\ Np &= 30 \quad (\text{MPCの予測時間}) \\ N_{back} &= 30 \quad (\text{考慮するBRSのステップ}) \\ r & = 7000 \text{km} \quad (\text{地球半径}) \\ P_f^{-1} &= \text{diag}(1/P_x^2, 1/P_y^2,0,0) \\ Q & = \boldsymbol{0} \\ R & = \mathbb{I} \\ M & = 0.01 \cdot \mathbb{I} \\ x(0) &= [0, -1000, 0, 0]^T \end{align}

簡単のため、今回は $Q=\boldsymbol{0}$ で燃料を最小化しつつターゲットの宇宙ステーションに接近する問題を選びました。

今回は、2つのフェーズに分かれたMPCを検証します。宇宙機2が宇宙機1に接近していくときに、まずは大きなKOZを定義して十分接近したのち、そのKOZの中に小さなKOZを新たに定義し、最終アプローチをするというシナリオを考えます。これらをそれぞれ phase 1/2と呼びます。^[2]

それぞれのKOZの楕円体の半径は、それぞれ $(P_x, P_y) = (200,100)$ と $(P_x, P_y) = (40,20)$ とします。

実験結果を以下の図に示します。灰と青の軌道たちは、それぞれその位置で制御を失ったと仮定したときのその後の宇宙機の軌道になります(灰: phase 1, 緑: phase 2)。図中の黒い丸が二つのphaseの切り替え地点になります。^[3]

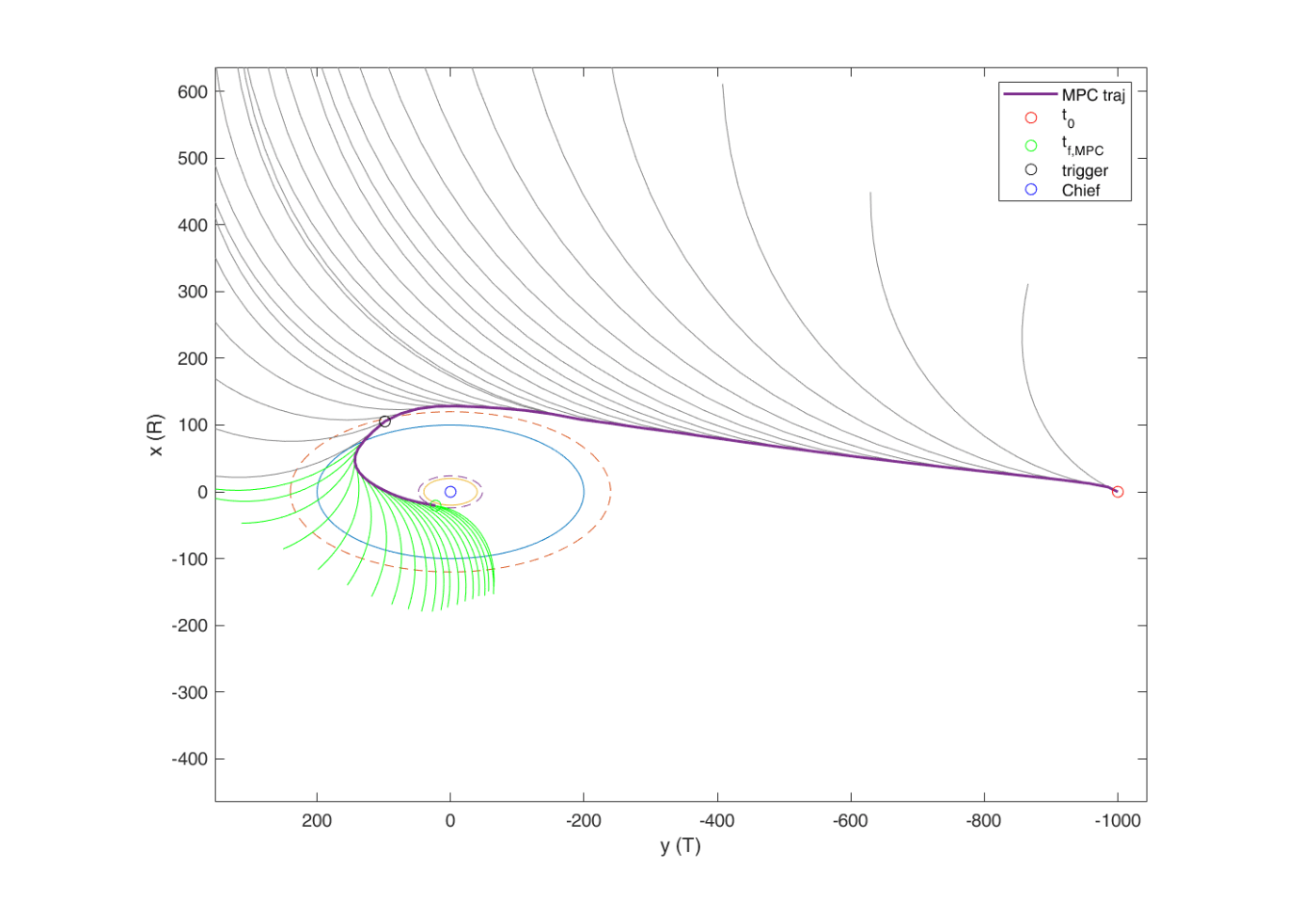
軌道を見て一目瞭然ですが、灰色の軌道は全て水色の大きなKOZの外側に、そして緑の軌道はすべてオレンジの小さなKOZの外側に伝播していっています。この特性を維持したまま、原点にある宇宙機1(chief)に接近しているのが確認できると思います。
これがPassive safetyの強さで、制御が止まっても最悪のケース(宇宙機同士の衝突)が自動で避けられるような制御履歴を作ることができます。

最後に

今回はPassive Safety という少し特殊な(確率論を使わない)ロバストな制御/MPC手法を紹介しました。現実的な意見として、ここまでの安全性/冗長性が欲しいシチュエーションに宇宙機以外があるかという話もあるかもしれませんが、reachable set をうまく活用することでオペレーション時の負荷を下げられる安心な軌道が作れることの旨味を感じて頂けたら嬉しいです。
この思想の先に、Abort-safetyと呼ばれる、部分的な故障が起きた際に残存するエンジン等で衝突回避を保証できるか、というより一般的な議論もあります(passive safetyはabort safetyの特殊ケースです)。ここまでくると、ハイブリッドシステムなどともしっかり接続されてくるので、また機会があればそのような話も執筆できればと思います。

参考文献

Marsillach, D.A., Di Cairano, S. and Weiss, A., 2022. Abort-Safe Spacecraft Rendezvous on Elliptic Orbits. IEEE Transactions on Control Systems Technology.
Marsillach, D.A., Di Cairano, S. and Weiss, A., 2020, July. Fail-safe rendezvous control on elliptic orbits using reachable sets. In 2020 American Control Conference (ACC) (pp. 4920-4925). IEEE.
Marsillach, D.A., Di Cairano, S., Kalabić, U. and Weiss, A., 2021, May. Fail-safe spacecraft rendezvous on near-rectilinear halo orbits. In 2021 American Control Conference (ACC) (pp. 2980-2985). IEEE.

脚注

まず、任意の点 $x$ から行列 $P$ で特徴づけられる楕円体との距離は $\rho^2 = x^T P^{-1} x$ で示されます。これを用いて、原点と機体を結ぶ線上にある、楕円体表面上の点は $x' = x / \rho$ と示すことができます。この点における楕円体への垂直な単位ベクトルは $\boldsymbol{n} = 2 P^{-1} x'$ 　と定義できるので、接超平面は $\boldsymbol{n}^T x = \boldsymbol{n} ^T x'$ 、つまり $\frac{\boldsymbol{n}^T}{ \boldsymbol{n} ^T x'} x = 1$ で表現できます。 $x'^T P^{-1} x'=1$ （楕円体上の点）に注意すると、上の式が導出できます。一般にN個の楕円体について同様の処理がしたい場合は、残念ながら解析的には $h$ は求まらず、二次錐計画を解くことになります（詳細は参考文献へ）。 ↩︎
厳密な話をすると、宇宙機が遠方にある場合、相対的な位置推定に対する誤差と、ダイナミクスの揺らぎに対する誤差を考慮するために、大きめにKOZ をとることで保守的な運用を行っています。KOZはあくまで我々が便宜上設定しているものであって、今回はある程度近づいたらより精度の良い推定ができる結果、KOZの領域を小さくできる、というようなシナリオを考えています。 ↩︎
今回のシミュレーションでは、それぞれのKOZの1.2倍の半径をとるような楕円体に侵入したらフェーズを切り替える/終了させることにしています。終盤に差し掛かると、制御されている軌道はどんどん原点(宇宙機1)に接近していくような軌道をとり、この想定される平常時の軌道がKOZの内部に入ってしまうと、"KOZに入らないはずの、reference の軌道から $u=0$ であろうがなかろうがKOZの中に侵入している" というトートロジーが起きてしまい、少し取り扱いが厄介です。こういったことが起こらないように、KOZの少し外側でフェーズ切り替えを行うことで今回は対応しています。最終的な目的地は原点だけど、原点を含むKOZには入りたくない、という絶妙な矛盾をMPCは解かされています...。具体的にいつフェーズを切り替えるかというのは結構悩ましい話です。 ↩︎