本記事は東京大学の村山裕和(https://www.linkedin.com/in/裕和-村山-9b42252b1/ )による寄稿です。
はじめに
本記事では、最適解が複数存在する場合について、複数の解を発見し、かつ最も良いものを制御入力として用いる為のモデル予測制御手法を紹介します。この手法により、局所最適解に陥る事で動作がスタックしてしまう事態が発生するのを防ぐ事が出来ます。
問題設定
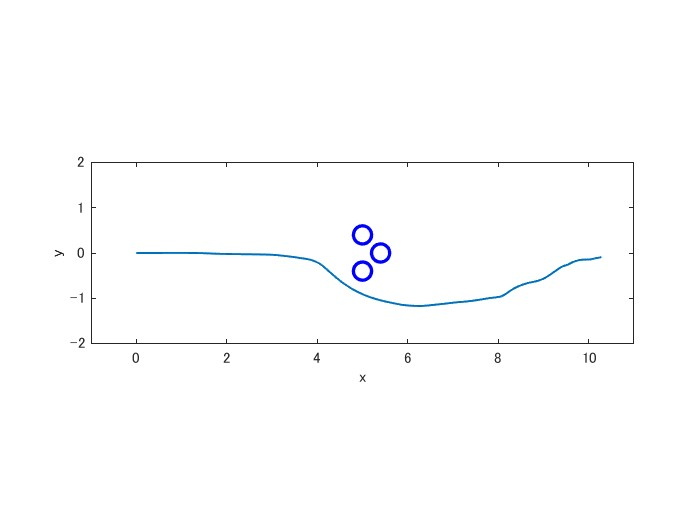
いきなりですが、次のような場面を想定してください。移動ロボットがスタット地点から真っすぐ先のゴール地点に到達する制御を考えます。以下の様に円形の障害物が複数並んでいるとします。

まず、普通のiLQRで制御してみましょう。評価関数はゴールへ向かう項、速度の上がり過ぎを抑える項、障害物を避ける項とします。すると以下の様な経路を取ります(初期値やパラメータを弄れば違った経路も取ります)。

この通り、障害物の間にハマってしまいます。何が起こっているのか説明します。まず、ロボットは手前二つの障害物を両方避けようとします。左右どちらにハンドルを切っても、一度片方の障害物に近づいて行く状況が発生するので、「真っすぐ進む」と言う制御になってしまいます。ハンドルを左右に切れないまま、正面にも障害物があるので、それにぶつからないように停止すると言う事態です。
人間であれば、「正面に進めば左右の障害物は避けられるけど、行き止まりになるな」「左右どちらかにハンドルを切り続ければ、一旦片方の障害物の方に向いてしまうけど、その後きちんと避けきれるな」と判断できます。つまり、「複数の最適解を求める」「複数の選択肢の中からより良い最適解を探す」事が出来るわけです。今日紹介するのは、そうした複数解の発見と比較をモデル予測制御で行う為の手法です。
Maximum Entropy-DDP/iLQR
前提として、Maximum Entropy-DDP/iLQR(以下、ME-DDP/iLQR)について説明します。
最適化問題の定義
まず、普通のDDP/iLQRからスタートします。システムの状態方程式と評価関数を以下の様に置きます。
x_{k+1}=f(x_{k},u_{k})\\
J = \phi(x_{T}) + \sum_{t=0}^{T-1} l_{t}(x_{t},u_{t})
x,u はそれぞれ状態変数と制御入力です。T は予測ステップ数です。\phi は終端コストと呼ばれる項であり、l_{t} はステージコストと呼ばれる項になります。通常のDDP/iLQRでは
u_{0}, \cdots , u_{T-1} = \argmin_{u_{0}, \cdots , u_{T-1}} J
の様に、評価関数を最小化する制御入力を具体的な数値として求めます。つまり、現在の状態(t=0)から T ステップ先までの状態及び入力についての何かしらの関数を最小化するように制御すると言う事です。ここまでが普通のDDP/iLQRです。(DDP/iLQRの具体的なアルゴリズムについての解説は割愛します)
ME-DDP/iLQRでは入力を幅のある確率分布として求めます。この際、解くべき最適化問題に以下の様に項を加えます。
\pi_{0}(u_{0}|x_{0}), \cdots , \pi_{T-1}(u_{T-1}|x_{T-1}) = \argmin_{\pi_{0}, \cdots , \pi_{T-1}} \mathbb{E}_{\pi} \left[ \phi(x_{T}) + \sum_{t=0}^{T-1} \left\{ l_{t}(x_{t},u_{t}) - \alpha H \left[ \pi_{t}(u_{t}|x_{t}) \right] \right\} \right]\\
H[\pi] = - \mathbb{E}_{\pi}[\log \pi] = - \int \pi(u|x) \log \pi(u|x) \ du
つまり、評価関数の期待値が最小になるような制御入力の確率分布を求めるわけです。各 \pi(u|x) は確率分布としての制御入力であり、状態変数が x である時の u の分布を意味します。これが入力 u の代わりとなります。H はシャノンの情報エントロピーと呼ばれるものであり、分布の分散が大きい(≒広がりが大きい)ほど大きな値を取ります。\alpha は設計者(人間)が決めるパラメータであり、つまるところ \alpha の値が大きいほど最適な確率分布が幅広い分布になります。逆に \alpha=0 とすると、分布の広がりが無い状態、つまりただの値が最適解となり、これは通常のDDP/iLQRと同じになります。
ベルマン方程式による表現
次に、この最適化問題をベルマン方程式に落とし込みます。ここで、次の様に V(x) を定めておきます。これは状態価値関数に当たるものです。今回の様に最適化問題にエントロピー項を追加した場合は「ソフト状態価値関数」と呼ばれます。
V_{t}(x_{t}) = \min_{\pi_{t}, \cdots , \pi_{T-1}} \mathbb{E}_{\pi} \left[ \phi(x_{T}) + \sum_{t=t}^{T-1} \left\{ l_{t}(x_{t},u_{t}) - \alpha H \left[ \pi_{t}(u_{t}|x_{t}) \right] \right\} \right]
要するに、t ステップ以降のみを考えた時の評価関数の期待値の最小値です。この V(x) を使うと、以下の様にベルマン方程式の形で最適化問題を表現する事が出来ます。
Q_{t}(x_{t},u_{t}) = l_{t}(x_{t},u_{t}) + V_{t+1}(f(x_{t},u_{t}))\\
V_{t}(x_{t}) = \min_{\pi_{t}} \mathbb{E}_{\pi_{t}} \left[ Q_{t}(x_{t},u_{t}) \right] - \alpha H \left[ \pi_{t}(u_{t}|x_{t}) \right]
Q(x,u) は元のベルマン方程式同様、行動価値関数に当たるものです。この様なベルマン方程式を「ソフトベルマン方程式」と呼びます。
最適化問題(ソフトベルマン方程式)の解
証明は割愛します(元論文の付録等をご覧ください)が、この時の最適解(最適な入力確率分布)は以下の様になります。
\begin{align}
\pi_{t}(u_{t}|x_{t}) &= Z(x_{t})^{-1} \exp \left( -\frac{1}{\alpha} \left[ V_{t+1}(f(x_{t},u_{t})) + l_{t}(x_{t},u_{t}) \right] \right)\\
&= Z(x_{t})^{-1} \exp \left( -\frac{1}{\alpha} Q_{t}(x_{t},u_{t}) \right)\\
Z(x_{t}) &= \int \exp \left( -\frac{1}{\alpha} \left[ V_{t+1}(f(x_{t},u_{t})) + l_{t}(x_{t},u_{t}) \right] \right) \ du_{t}\\
&= \int \exp \left( -\frac{1}{\alpha} Q_{t}(x_{t},u_{t}) \right) \ du_{t}\\
\end{align}
これはボルツマン分布と呼ばれる分布です。また、V_{t}(x_{t}) と Q_{t}(x_{t},u_{t}) の間には次のような関係が成り立ちます。
V_{t}(x_{t}) = -\alpha \log \int \exp \left( -\frac{1}{\alpha} Q_{t}(x_{t},u_{t}) \right) \ du_{t}
これを V_{t}(x_{t}) と Z(x_{t}) の関係式として書き直すと、次の様になります。
V_{t}(x_{t}) = - \alpha \log Z_{t}(x_{t})
解の計算
ただ、実はME-DDP/iLQRではこのボルツマン分布そのものを求める事は出来ません。代わりにボルツマン分布を正規分布で近似した分布を求める事になります。以下ではその経緯を説明します。
天下り的ではありますが、まずボルツマン分布の正規分布近似について説明します。Q_{t}(x_{t},u_{t})=V_{t+1}(f(x_{t},u_{t}))+ l_{t}(x_{t},u_{t}) を、何らかの値 $ \bar{x_{t}} , \bar{u_{t}}$ 周辺で以下の様に二次近似する事を考えます。偏微分とヘッシアンを右下に文字を添えて表しています。
\begin{align}
\pi_{t}(u_{t}|x_{t}) &= Z(x_{t})^{-1} \exp \left( -\frac{1}{\alpha} Q_{t}(x_{t},u_{t}) \right)\\
& \cong Z(x_{t})^{-1} \exp \left( -\frac{1}{\alpha} \left[Q_{t}(\bar{x}_{t},\bar{u}_{t}) + \frac{1}{2} \delta u_{t} Q_{t,uu} \delta u_{t} + Q_{t,u} \delta u_{t} + \frac{1}{2} \delta x_{t} Q_{t,xx} \delta x_{t} + Q_{t,x} \delta x_{t} + \delta x_{t} Q_{t,xu} \delta u_{t} \right] \right)\\
Z(x_{t}) & = \int \exp \left( -\frac{1}{\alpha} Q_{t}(x_{t},u_{t}) \right) \ du_{t} \\
& \cong \int \exp \left( -\frac{1}{\alpha} \left[Q_{t}(\bar{x}_{t},\bar{u}_{t}) + \frac{1}{2} \delta u_{t} Q_{t,uu} \delta u_{t} + Q_{t,u} \delta u_{t} + \frac{1}{2} \delta x_{t} Q_{t,xx} \delta x_{t} + Q_{t,x} \delta x_{t} + \delta x_{t} Q_{t,xu} \delta u_{t} \right] \right) \ d \delta u_{t}
\end{align}
この分布は平均が \bar{u_{t}}、分散が \alpha Q_{t,uu}^{-1} の正規分布となります。問題はこの\bar{u_{t}} 及びそれに対応する \bar{x_{t}} をどこに取れば上手く近似出来るのかという事です。
ここで、正規分布の特徴について考えてみましょう。正規分布は値が平均の時に曲線が丁度山の頂上(極大と言った方が良いでしょうか)になります。一方で、ボルツマン分布にも山の頂上(極大?)の部分が存在すると思われます(もし存在しないとしたら、それは恐らく値としての最適解も存在しない場合なので、ここでは無視します)。この頂上が一致すれば、上手く分布が重なりそうです。
では、ボルツマン分布の頂上、つまり確率が極大になっている点はどこにあるのかを考えます。元のボルツマン分布において、分母Z(x_{t})はu_{t}に依らない値ですから、頂上の位置は分子 \exp \left( -\frac{1}{\alpha} Q_{t}(x_{t},u_{t}) \right) によって決まります。この分子の値が極大になる点、つまり、Q_{t}(x_{t},u_{t}) が極小となる u_{t}を \bar{u_{t}} とすれば良いわけです。
結局、行動価値関数を最小化する u_{t} を求めるわけですから、通常のDDP/iLQRとやる事は同じです。エントロピー項を加えた影響で途中式がかなりややこしくなっていますが、実は式変形して行くと結局通常のDDP/iLQRと同じアルゴリズムにたどり着きます。ここら辺の詳しい途中式は元論文のAppendix Bをご覧ください。尚、分散 \alpha Q_{t,uu}^{-1} は \bar{u_{t}} を求める過程で勝手に求まります。これで平均と分散が求まる、すなわち目的とする正規分布が求まります。
結局、ME-DDP/iLQRで使用する計算アルゴリズム自体は通常のDDP/iLQRとほぼ同じです。ただ、裏にある数式に変化があり(エントロピー項が加わる)、最終的に求める解を分布にして算出すると言う点が違います。
Multimodal Maximum Entropy-DDP/iLQR
マルチモーダルな解
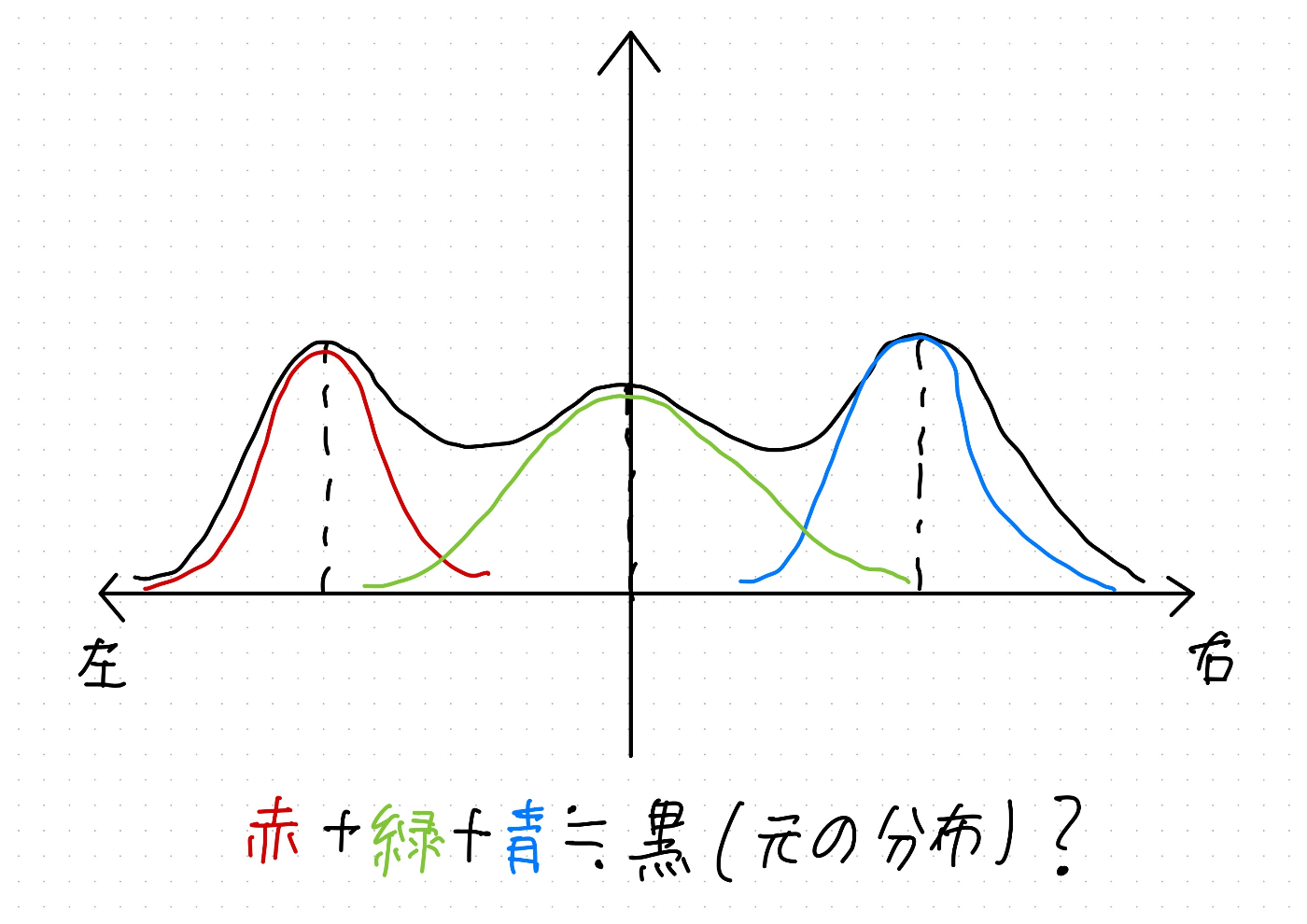
ここまで来たらいよいよマルチモーダルなDDP/iLQRの説明に入ります。マルチモーダルの意味から確認します。"multimodality"とはすなわち「多峰性」を意味します。誤解を恐れず言ってしまえば、確率分布ならば下のイラストの様に極大/山となる点が複数ある状態の事です。逆に、ユニモーダルとは、極大が一つしか無い、いわば山が一つしか無い状態です。

当記事冒頭で説明した問題設定を思い出してください。例えば、ハンドルを左右どっちに切るかを制御入力として横軸に取れば、最適な制御入力分布はざっくりと以下の様になる事が直感的にわかると思います。

まず、左右の障害物を等しく避けようとして真っすぐ進み行き止まりに当たってしまうパターン(真ん中の山)、右に避けるパターン(右の山)、左に避けるパターン(左の山)の3つです。ただし、この分布を直接ME-DDP/iLQRで算出するのは不可能です。ME-DDP/iLQRで求まるのはあくまで本当の解であるボルツマン分布を極大付近で局所的に近似した正規分布であり、正規分布はユニモーダル(マルチモーダルではない)です。つまるところ、1つの正規分布ではマルチモーダルな分布のうち、1つの山しか近似出来ません。
ユニモーダル+ユニモーダル=マルチモーダル
そこで、ユニモーダルな分布を複数重ねる事でマルチモーダル分布を表現出来ないかと考えます。例えば、今回の例であれば、ME-DDP/iLQRによって次の図の様な3つの正規分布が求められれば、それらを重ね合わせる事で真のマルチモーダルな分布を近似する事が出来そうです(。
重ね合わせ計算
ここでは、正規分布解の重ね合わせを具体的に数式で導出して行きたいと思います。まず、ME-DDP/iLQRによって N 個の最適解 \pi_{t}^{1}(u_{t}|x_{t}), \cdots , \pi_{t}^{N}(u_{t}|x_{t}) が求まったとします。また、各分布の平均 \bar{u_{t}}^{1}, \cdots , \bar{u_{t}}^{N} 及びそれに従った時の状態変数の平均 \bar{x_{t}}^{1}, \cdots , \bar{x_{t}}^{N} の周囲で近似した際のZ(x_{t})の値を次のように置きます。
\begin{align}
z^{n}(x_{t}) & = \int \exp \left( -\frac{1}{\alpha} Q_{t}^{n}(x_{t},u_{t}) \right) \ du_{t} \\
& \cong \int \exp \left( -\frac{1}{\alpha} \left[Q_{t}^{n}(\bar{x}_{t}^{n},\bar{u}_{t}^{n}) + \frac{1}{2} \delta u_{t} Q_{t,uu}^{n} \delta u_{t} + Q_{t,u}^{n} \delta u_{t} + \frac{1}{2} \delta x_{t} Q_{t,xx}^{n} \delta x_{t} + Q_{t,x}^{n} \delta x_{t} + \delta x_{t} Q_{t,xu}^{n} \delta u_{t} \right] \right) \ d \delta u_{t}
\end{align}
この時、各正規分布解及び各正規分布解に対応する V_{t}^{n}(x_{t}) はME-iLQR同様に以下の様に表せます。
\pi_{t}^{n}(u_{t}|x_{t}) = z^{n}(x_{t})^{-1} \exp \left( -\frac{1}{\alpha} \left[Q_{t}^{n}(\bar{x}_{t}^{n},\bar{u}_{t}^{n}) + \frac{1}{2} \delta u_{t} Q_{t,uu}^{n} \delta u_{t} + Q_{t,u}^{n} \delta u_{t} + \frac{1}{2} \delta x_{t} Q_{t,xx}^{n} \delta x_{t} + Q_{t,x}^{n} \delta x_{t} + \delta x_{t} Q_{t,xu}^{n} \delta u_{t} \right] \right) \\
V_{t}^{n}(x_{t}) = - \alpha \log z^{n}(x_{t})
これはつまるところ、行動価値関数を二次形式で近似(≒最適な分布解を局所的に正規分布で近似)した時の状態価値関数です。
ここで、真の状態価値関数 V_{t}(x_{t}) を考えます。複数の解があり、それぞれその解の付近で近似した関数 V_{t}^{n}(x_{t})を置いたわけです。これらは、このステップ以降取りうる評価関数値の候補と言えます。その上で、状態価値関数とはそのステップ以降の評価関数の最小値を表す関数です。つまり、V_{t}^{1}(x_{t}), \cdots , V_{t}^{N}(x_{t}) の中から最小となるものを選ぶことで、元の V_{t}(x_{t}) を近似する事を考えます。ここで、要素の最小値を近似する関数としてlog-sum-exp関数を用います(機械学習において良く使われるようです)。
\begin{align}
V_{t}(x_{t}) &= \min \left\{ V_{t}^{1}(x_{t}), \cdots , V_{t}^{N}(x_{t}) \right\}\\
& \cong -\alpha \log \sum_{n=1}^{N} \exp \left( -\frac{1}{\alpha} V_{t}^{n}(x_{t}) \right)
\end{align}
後々のため、式変形して次の様にしておきます。
\exp \left( -\frac{1}{\alpha} V_{t}(x_{t}) \right) = \sum_{n=1}^{N} \exp \left( -\frac{1}{\alpha} V_{t}^{n}(x_{t}) \right)
また、この式を Z(x_{t}) 及び z^{1}(x_{t}), \cdots , z^{N}(x_{t}) を使って書き換えると、以下の様になります。
Z(x_{t}) = \sum_{n=1}^{N} z^{n}(x_{t})
この議論は t=0 \sim T 全てにおいて同様に成り立ちます。
それでは最後に、これらの関係式を利用して真のマルチモーダルな解 \pi_{t}(u_{t}|x_{t}) を、正規分布により局所近似した解 \pi_{t}^{n}(u_{t}|x_{t}) の組み合わせに変形して行きたいと思います。
\begin{align}
\pi_{t}(u_{t}|x_{t}) &= Z(x_{t})^{-1} \exp \left( -\frac{1}{\alpha} \left[ V_{t+1}(f(x_{t},u_{t})) + l_{t}(x_{t},u_{t}) \right] \right)\\
&= Z(x_{t})^{-1} \sum_{n=1}^{N} \exp \left( -\frac{1}{\alpha} \left[ V_{t+1}^{n}(f(x_{t},u_{t})) + l_{t}(x_{t},u_{t}) \right] \right)\\
&= \sum_{n=1}^{N} \frac{z^{n}(x_{t})}{Z(x_{t})} z^{n}(x_{t})^{-1} \exp \left( -\frac{1}{\alpha} \left[ V_{t+1}^{n}(f(x_{t},u_{t})) + l_{t}(x_{t},u_{t}) \right] \right)\\
&= \sum_{n=1}^{N} \frac{z^{n}(x_{t})}{Z(x_{t})} \pi_{t}^{n}(u_{t}|x_{t})
\end{align}
z^{n}(x_{t})/Z(x_{t}) の合計は先ほどの議論から1となります。これはつまり、マルチモーダルな分布解の各山付近で局所近似した正規分布に対し、重み z^{n}(x_{t})/Z(x_{t}) で加重平均を取れば(≒重みを付けて重ね合わせれば)元のマルチモーダルな分布を再現できるという事です。
これでマルチモーダルな最適分布解を求めることが出来ます。この分布に従うように次の制御計算における初期値をサンプリングすれば、最終的に求まった解によりマルチモーダルな分布全体を賄える可能性が上がるわけです(サンプリングである以上、確実にとは言えません)。
ちなみに、この様に正規分布(ガウス分布)を重ね合わせたモデルを混合ガウスモデル(GMM:Gaussian Mixture Model)と言います。元々はクラスタリングで使われるものの様です。
確率分布は何のため?
ここまでやってきて言うのも何ですが、確率分布そのものを制御入力にするわけではありません。では何に確率分布 \pi(u|x) を使うかと言うと、解のサンプリングに使います。DDP/iLQRは勾配情報を用いて解を最適解に収束させていく手法です。その為、最適解が複数存在する場合、初期解によって収束後の解が異なる事もあります。逆に、全ての解が同じ値に収束してしまう事もあります。マルチモーダルな分布を捉えたいのであれば、それは好ましい事ではありません。そこで、確率分布に基づく乱数生成を利用する事で初期解を適度にばらけさせているのです。また、そうすれば初期解は最適解そのものとはズレた値になりますから、まだ発見できていない新たな最適解に収束する可能性も残しています。このように、既存の最適解付近に初期解をバランス良く配置しつつも、新たな解を見つける可能性も残すと言う仕組みになっています。これがMME-DDP/iLQRです。
尚、実際に制御入力として用いるのは、発見された最適分布解 \pi_{0}^{1}(u_{0}|x_{0}) \sim \pi_{0}^{N}(u_{0}|x_{0}) の内、最も評価関数を最小化出来る分布の平均値になります。
以上をまとめると、分布を基に解を探索し、見つかった最適解の中から最適な物を選ぶと言うのがMME-DDP/iLQRの仕組みになります。
MME-DDP/iLQRを使ってみる
では最後に、MME-DDP/iLQRを冒頭の問題に適用してみましょう。すると以下の様に局所最適解にハマらずに避けてくれます。
最後に
論文内ではMME-DDPと言う名称しか使われていませんが、テンソル項を考慮していないのでDDPではなく正確にはiLQRです。ただDDPもiLQRもアルゴリズムは99%同じなので、自分はMME-DDP/iLQRと書きました。まあ好きな方で呼べば大丈夫だと思います()。
参考文献
この記事は以下の論文の手法を紹介・解説しております。何故か論文中に登場する定理の証明はarxiv版にしか載っていません。
- Maximum Entropy Differential Dynamic Programming (O. So, Z. Wang and E. A. Theodorou, ICRA, 2022)
- Maximum Entropy Differential Dynamic Programming (O. So, Z. Wang and E. A. Theodorou, arxiv ,2021)






Discussion