拡散モデルを用いたモデルベース最適化
本記事は名古屋大学の本田康平(https://kohonda.github.io/ )による寄稿です.
はじめに
近年,拡散モデルの発展によって,非常に複雑な分布から忠実度の高いサンプルを生成することが可能となりました.最も一般的な拡散モデルの用途としては,画像や音声のような教師データを用意し,そのデータの分布のモデルを学習し,そのモデルを用いて新しいデータを生成することが挙げられます.ロボティクスにおいても同様の研究は多数存在し,ロボットの軌道教師データを用意・学習し,そのデータを用いて新しい軌道を生成することが行われています .
一方,モデル予測制御をはじめとしたモデルベース最適制御の文脈においては,教師データの代わりに制御対象のダイナミクス・コスト関数・制約条件が最適制御問題として与えられており,これらの情報を用いて最適な制御入力を計算することが求められます.今回紹介する論文である,Model-Based Diffusion for Trajectory Optimization (MBD) (preprint, 2024) は,このようなモデルベース最適制御問題において,拡散モデルを用いて最適制御入力を算出する方法を提案しています .すなわち,拡散モデルを最適化ソルバーとして用いる研究となります.なお,この拡散モデルベースのソルバーMBDは最適化問題の勾配情報を用いない0次最適化手法であり,MPPIなどの手法の発展系となります (MPPIについてはこちら).
※ 本論文は現在preprintであり,内容が変更される可能性があります.
拡散モデルについて
本記事では拡散モデルについての詳細は説明しませんが,簡単にその目的とアイデアを述べます.拡散モデルの目的は,何らかのデータ集合が与えられた時に,そのデータ集合の未知の真の分布を近似するような確率分布モデルp_\theta(x)を学習し,その分布からサンプルを生成することです.真の分布は一般に非常に複雑な形状であり,ガウス分布や混合ガウス分布といった,パラメトリックな分布では表現能力が不足します.そこで,拡散モデルは,データ集合にノイズを加え,そのノイズを復元するようなモデルを学習することによって,真の分布を近似します.その結果,拡散モデルはマルチモーダルな分布に対しての表現力が高くなります.
問題設定
本論文では,一般的な拡散モデルの問題設定とは異なり,データ集合の代わりに,以下の最適制御問題がユーザーによって与えられていると仮定します.
\begin{align}
\min_{x_{1:T}, u_{1:T}} & \quad J(x_{1:T}, u_{1:T}) = l_T(x_T) + \sum_{t=1}^{T-1} l_t(x_t, u_t) \nonumber \\
\text{s.t.}
& \quad x_0 = x_{\text{init}} \nonumber \\
& \quad x_{t+1} = f(x_t, u_t), \quad \forall t = 0, 1, \ldots, T-1 \nonumber \\
& \quad g(x_t, u_t) \leq 0, \quad \forall t = 0, 1, \ldots, T-1 \nonumber
\end{align}
ここで,x_t \in \mathbb{R}^{n_x}は状態,u_t \in \mathbb{R}^{n_u}は制御入力,l_t(x_t, u_t)はコスト関数,f(x_t, u_t)はダイナミクス,g(x_t, u_t)は制約条件を表します.また,x_{\text{init}}は初期状態,Tは最適制御の時間ホライズンです.
従来は,このような最適制御問題を解くために,勾配情報を用いる最適化手法が用いられてきました.しかしながら,コスト関数やダイナミクスが非線形であったり,微分不可能な場合には解を求めることが非常に難しくなります.そこで,Control as Inferenceのように,最適制御問題から最適な制御入力の確率分布を定義し,その分布をパラメトリックに近似,もしくはその分布からサンプルするような研究が盛んにおこなわれています.
すなわち,上記の最適制御問題から最適な分布の確率密度p(Y) (ここでY = \{x_{1:T}, u_{1:T}\}) を以下のように定義します.
\begin{align}
& p(Y) \propto p_d(Y) p_J(Y) p_g (Y) \tag{1}\\
& p_d(Y) \propto \prod_{t=0}^{T-1} \mathbb{1} ({x_{t+1} = f(x_t, u_t)}) \nonumber \\
& p_J(Y) \propto \exp(-\frac{J(Y)}{\lambda}) \nonumber \\
& p_g(Y) \propto \prod_{t=0}^{T-1} \mathbb{1} (g(x_t, u_t) \leq 0) \nonumber
\end{align}
p_d(Y)はダイナミクスの確率密度,p_J(Y)はコスト関数の確率密度,p_g(Y)は制約条件の確率密度を表します.また,\lambdaはハイパーパラメータです.p_J(Y)はボルツマンと呼ばれ,コスト関数が小さいほど大きな確率密度を持つように設計されています.
ここで重要なのは,p(Y)は一つのサンプルYが得られた時に確率密度を計算できるのみであり,一般にp(Y)から直接サンプルすることは困難です.そこで,Control as Inferenceなどでは,不定なp(Y)を,何らかのサンプル可能な確率分布q(Y)で近似し,その分布からサンプルを得ます (いわゆる変分推論) が,本論文では,拡散モデルを用いてp(Y)からサンプルを得ることを提案しています.
提案手法
概要
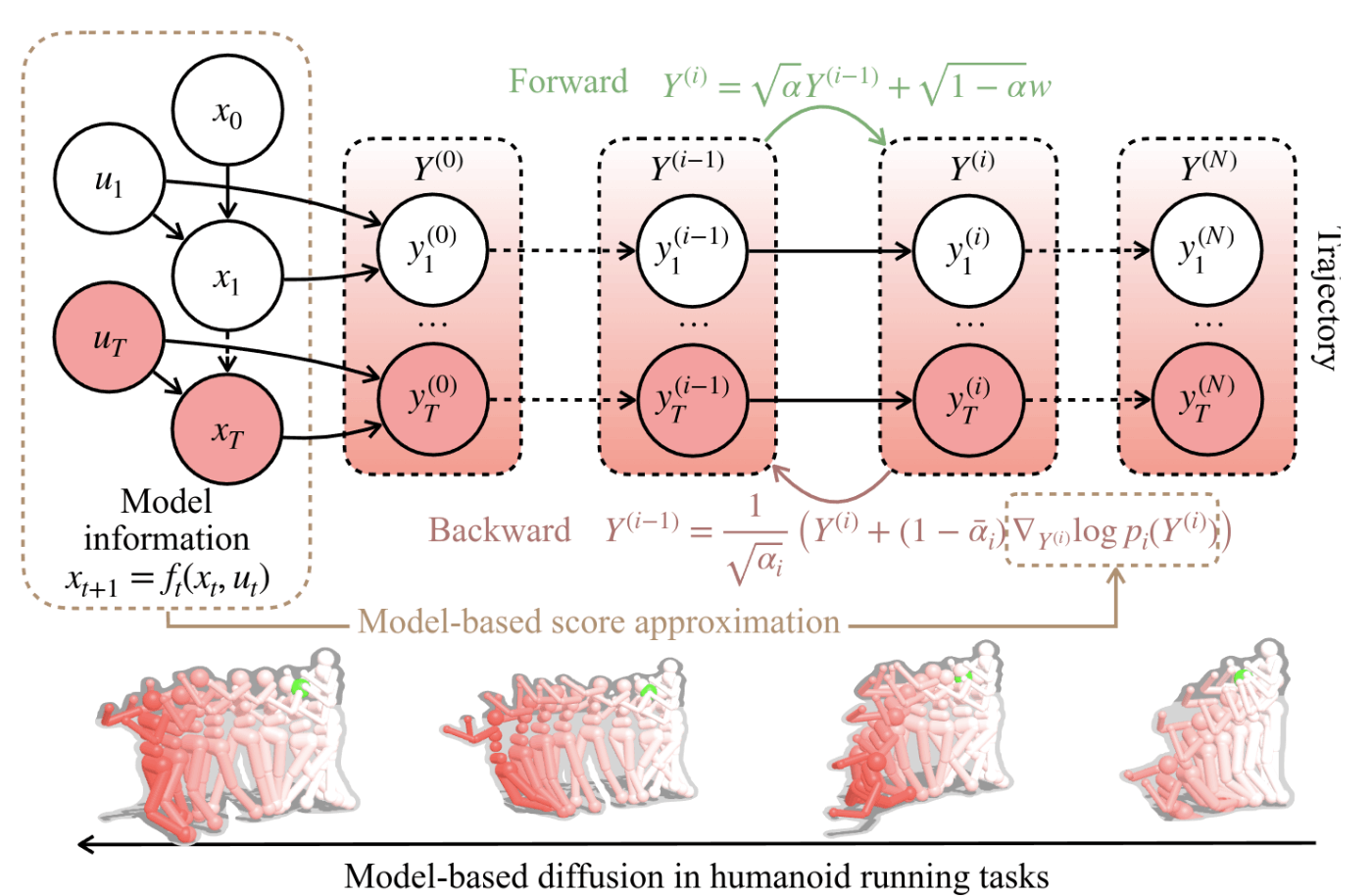
図1 Model-based Diffusion (MBD)における拡散過程
図1のような拡散過程を仮定します.すなわち,最適分布からのサンプルY^0 \sim p(Y)をガウス分布p(Y^i | Y^{i-1})=\mathcal{N}(\sqrt{\alpha_i} Y^i, (1-\alpha_i) I)によってN回ノイジングする過程をForward processとし,逆にデノイジングp(Y^{i-1} | Y^i)を行う過程をBackward processとします.\alpha_iはハイパーパラメータであり,0 < \alpha_i < 1を満たすものとします.
Forward processはガウス分布の性質とマルコフ性から,i=0から任意のiまでの確率もガウス分布になるため,p(Y^i | Y^0)は以下のように表されます.
\begin{align}
& p(Y^i | Y^0) = \mathcal{N}(\sqrt{\bar{\alpha}_i} Y^0, (1-\bar{\alpha}_i) I) \tag{2}
\end{align}
ここで,\bar{ \alpha} _ i = \prod _ {j=0} ^{i} \alpha_jです.
Backward processは,拡散モデルの代表格であるDDPMではデノイジングはガウス分布からのサンプル,スコアベースモデルではランジュバンモンテカルロ法として定式化されますが,本論文では,以下のように定式化します.(文中ではMontecarlo Score Ascentと呼ばれています.)
\begin{align}
& Y^{i-1} = \frac{1}{\sqrt{\alpha_i}} (Y^i + (1-\bar{\alpha}_i) \nabla_{Y^i} \log p(Y^i)) \tag{3}
\end{align}
式 (3) はスコアベースモデルの定式化に近いものの,ノイズ項が含まれてない点が異なります.(予想の域ですが,ノイズ項を含めると,うまく収束してくれないため,ヒューリスティックに取り除いたのだと思われます.)
ここでまず,どのように実際に式 (1)の最適分布からサンプルを行うかを整理します.式 (2)のForward processはNが十分に大きく,\alpha_Nが十分に小さい時に,N回ノイジングした,p(Y^N | Y^0)が\mathcal{N}(0, I)に収束することが知られています.そこで,以下の流れでサンプルを得ます.
-
Y^N \sim N(0, I)をサンプル
- 式 (3)のBackward Processによって,Y^{i}からY^{i-1}にデノイジング (i=N, \ldots, 1と繰り返す)
- 最適分布からのサンプルY^0 \sim p(Y^0)が得られる
すなわち,式 (3)を計算することができれば,最適分布からのサンプルを得ることができます.ただし,式 (3)のスコア\nabla_{Y^i} \log p(Y^i)を計算する必要があります.一般的なデータドリブンの拡散モデルでは,このスコアを学習によって近似しますが,MBDでは,データの代わりに最適制御問題が与えられているので,スコアを式 (1)を用いて近似していきます.
※ 繰り返しになりますが,今回の問題設定では,式 (1)の最適分布の確率密度p(Y)は一つのサンプルYが得られた時に計算することができます.(データのみ与えられた場合の拡散モデルでは計算することができません.)
スコア関数\nabla_{Y^i} \log p(Y^i)の近似
はじめに,スコア関数を式変形していきます.
\begin{align}
\nabla_{Y^i} \log p(Y^i)
&= \frac{\nabla_{Y^i} p(Y^i)}{p(Y^i)} \nonumber \\
&= \frac{\nabla_{Y^i} \int p(Y^i | Y^0) p(Y^0) dY^0}{\int p(Y^i | Y^0) p(Y^0) dY^0}
\quad (\because ベイズの定理と周辺化) \nonumber \\
&= \frac{\int \nabla_{Y^i} p(Y^i | Y^0) p(Y^0) dY^0}{\int p(Y^i | Y^0) p(Y^0) dY^0} \tag{4}
\end{align}
ここで,式 (2) より,\nabla_{Y^i} p(Y^i | Y^0)はガウス分布の確率密度関数を用いて計算することができるので,式 (4)は以下のように更に展開されます.
\begin{align}
\nabla_{Y^i} \log p(Y^i)
&= \frac{\int -\frac{Y^i - \sqrt{\bar{\alpha}_i} Y^0}{1-\bar{\alpha}_i}p(Y^i | Y^0) p(Y^0) dY^0}{\int p(Y^i | Y^0) p(Y^0) dY^0} \nonumber \\
&= -\frac{Y^i}{1-\bar{\alpha}_i} + \frac{\sqrt{\bar{\alpha}_i}}{1-\bar{\alpha}_i} \underbrace{\frac{\int Y^0 p(Y^i | Y^0) p(Y^0) dY^0}{\int p(Y^i | Y^0) p(Y^0) dY^0}}_{期待値計算に持ち込む} \tag{5} \\
\end{align}
式 (5)の第2項目を眺めると,Y^0の積分が分母分子に含まれているため,解析的に計算することは難しいです.このような場合はY^0に関する期待値計算に持ち込み,モンテカルロ法による推定を行いたいところです.期待値に持ち込むためには,Y^0をサンプリングできる分布の確率密度,Y^0 \sim p(Y^0 | *)が積分内に含まれている必要があります.(\because \int f(x) p(x) dx = \mathbb{E}_{x \sim p(x)}[f(x)]) しかしながら,式 (5)の分母分子の積分内部にはp(Y^i | Y^0)とp(Y^0)しか含まれておらず,Y^0を実際にサンプリングできる分布が含まれず,このままでは期待値計算ができません.(p(Y^0)は不定の最適分布の確率密度であり,Y^0をサンプリングすることができません.) そこで,p(Y^i | Y^0)を以下のように変形することによって,Y^0に関する確率分布のようにみせかけてしまいます.
\begin{align}
p(Y^i | Y^0)
& = \mathcal{N}(\sqrt{\bar{\alpha}_i} Y^0, (1-\bar{\alpha}_i) I) \quad (式 (2)) \nonumber \\
\Leftrightarrow Y^i
& = \sqrt{\bar{\alpha}_i} Y^0 + \sqrt{1-\bar{\alpha}_i} \epsilon, \; \epsilon \sim \mathcal{N}(0, I) \quad (\text{Reparameterization trick}) \nonumber \\
\Leftrightarrow Y^0
& = \frac{1}{\sqrt{\bar{\alpha}_i}} Y^i - \sqrt{\frac{1}{\bar{\alpha}_i}-1} \epsilon, \; \epsilon \sim \mathcal{N}(0, I) \nonumber \\
Y^0 &\sim \bar{p}(Y^0 | Y^i) = \mathcal{N}(\frac{1}{\sqrt{\bar{\alpha}_i}} Y^i, \frac{1}{\bar{\alpha}_i}-1) \quad (ガウス分布の対称性) \tag{6}
\end{align}
上式 (6)より,Y^0をサンプリングすることができる\bar{p}(Y^0 | Y^i)が得られたので,式 (5) は以下のように期待値計算に落とし込まれます.
\begin{align}
\nabla_{Y^i} \log p(Y^i)
&= -\frac{Y^i}{1-\bar{\alpha}_i} + \frac{\sqrt{\bar{\alpha}_i}}{1-\bar{\alpha}_i} \frac{\int Y^0 p(Y^i | Y^0) p(Y^0) dY^0}{\int p(Y^i | Y^0) p(Y^0) dY^0} \nonumber \\
&= -\frac{Y^i}{1-\bar{\alpha}_i} + \frac{\sqrt{\bar{\alpha}_i}}{1-\bar{\alpha}_i} \frac{\mathbb{E}_{Y^0 \sim \bar{p}(Y^0 | Y^i)}[Y^0 p(Y^0)]}{\mathbb{E}_{Y^0 \sim \bar{p}(Y^0 | Y^i)}[p(Y^0)]} \nonumber \\
&= -\frac{Y^i}{1-\bar{\alpha}_i} + \frac{\sqrt{\bar{\alpha}_i}}{1-\bar{\alpha}_i} \frac{\sum_{Y^0} Y^0 p(Y^0)}{\sum_{Y^0}p(Y^0)}, \; Y^0 \sim \bar{p}(Y^0 | Y^i) \quad(モンテカルロ法) \tag{7}
\end{align}
式 (7)より,スコア関数\nabla_{Y^i} \log p(Y^i)を,Y^iと式 (1)の最適分布の確率密度p(Y^0)によって推定することができました.その結果,式 (3) のBackward Processによってデノイジング計算が可能となります.
さて,ここで式 (7)の\frac{\sum_{Y^0} Y^0 p(Y^0)}{\sum_{Y^0}p(Y^0)}, \; Y^0 \sim \bar{p}(Y^0 | Y^i)を改めて見ると,p(Y^0)の最適分布が\exp(-J/\lambda)で定義されていることから,MPPIと同様の計算,すなわち,Softmax計算を行うことになります.つまり,MPPIはある既定の分散レベルにおけるスコア関数の一部を計算しており,MBDはMPPIを複数回解くことによって,デノイジングを行い,最適分布からのサンプルを得る手法である,ということになります.
実験結果
以下は論文中に記載されていた実験結果の一部です.また,ソースコードは著者らによって公開されています.(https://github.com/LeCAR-Lab/model-based-diffusion)
拡散モデルが最適化計算にどのような良さを提供するのか?
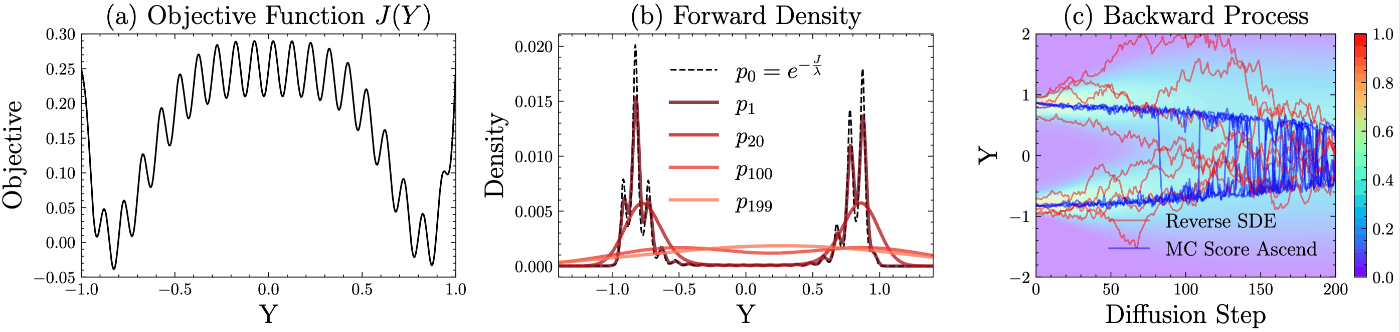
図2 拡散モデルが最適化計算にどのような良さを提供するのか?
拡散モデルの利点として,生成されるサンプルが真の分布のマルチモダリティ (解の多様性) を捉えやすいことが挙げられます.最適制御的の視点では,複数の局所解 (モード) がある時に,一つのモードに捉えられない,つまり,局所最適を回避できる可能性が高まります.
図2は簡単な問題においてその可能性を示唆しています.(a) は最適化問題のコスト関数,(b)は式 (1)によって定義される最適密度を破線で,デノイジング計算によって得られた確率分布を実践で表しています.(b)から分かるとおり,最適分布は複数のモード (局所解) を有していますが,拡散ステップを200程に設定すると,それらの複数のモードを捉えることができています.(※ 実際にパラメトリックな確率密度が計算できるわけではありません.)
また,図2の(c)は一般的な拡散モデルのBackward processで用いられるReverse SDEと,本手法式 (3)のノイズ項なしのMontecarlo Score Ascentのデノイジング過程における軌跡が比較されていますが,提案手法はノイズによるモードからの脱出が促進されないことから,複数のモードのうち,大きな確率密度のモードへ素早く収束していることが確認できます.制御の観点からは,解の多様性よりも素早い収束の方が望ましいのかもしれません.
ベンチマークによる評価

図3 Demo: Humanoid Running
いくつかのタスクによってベンチマークが行われています.図3はHumanoid Runningのデモですが,gifの最初のノイズを多分に含んだグチャクチャな軌跡から,徐々にデノイジングされ,最適な軌跡に収束していく様子が確認できます.
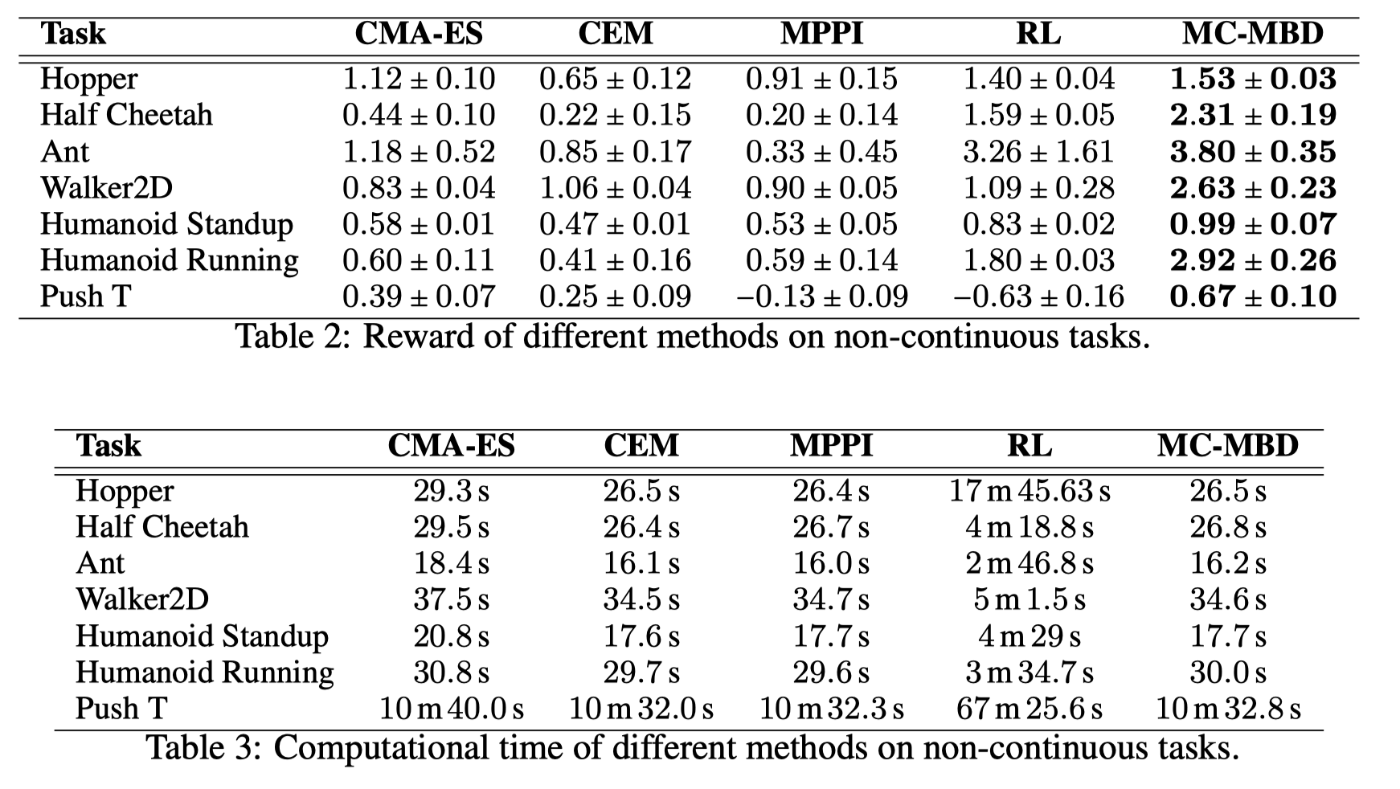
図4 ベンチマーク
図4のベンチマーク結果 (Table 2) を見ると,全てのタスクで,MPPIやRL (PPO) よりも性能が良いことが示されています.Table 3では計算時間の比較がなされており,こちらでも提案手法が最も高速であると主張されています.しかしながら,式 (7) を見ても分かるとおり,MBDは拡散ステップN回分MPPIの計算をする必要があるため,MPPIよりも高速であるとは考えづらいです.また,RLとの比較は推論時間ではなく,学習時間での比較となっており,直接的な比較に意味があるのかは疑問が残ります.
その他
詳細は省略しますが,その他にも以下のいくつかの実験が論文中では行われています.詳しくは論文を参照してください.
- 教師データによるガイダンスによるsparse-rewardタスクや不等式制約への対応
- 最適制御ソルバーではなく,ブラックボックス最適化への利用




Discussion