宣伝
拙著「PythonとCasADiで学ぶモデル予測制御 (KS理工学専門書) 」が発売されました!

是非こちらも読んでいただければ幸いです。
クアッドローターの非線形MPC制御
https://youtu.be/cBNrw5Myv04
全体概要
- 非線形MPCを用いてドローン(クアッドローター)を空中で回転させることを目指します
- ここで扱うクアッドローターとは、以下の仮定を満たすものです
- 機体フレームは剛体
- 機体フレームは対称
- 機体フレームの重心と機体座標系の原点は一致している
- プロペラは剛体
- 推力と抗力はプロペラ回転数の2乗に比例する
- 各プロペラごとに回転する向きは一定
- 非線形の連続時間最適化問題は直行コロケーション法(orthogonal collocation method)により解きます
クアッドローターのダイナミクス
ここでは、クアッドローターのダイナミクスをオイラー・ラグランジュの運動方程式により導出します。(ローターごとに\omega, \tauの向きが異なることに注意!)
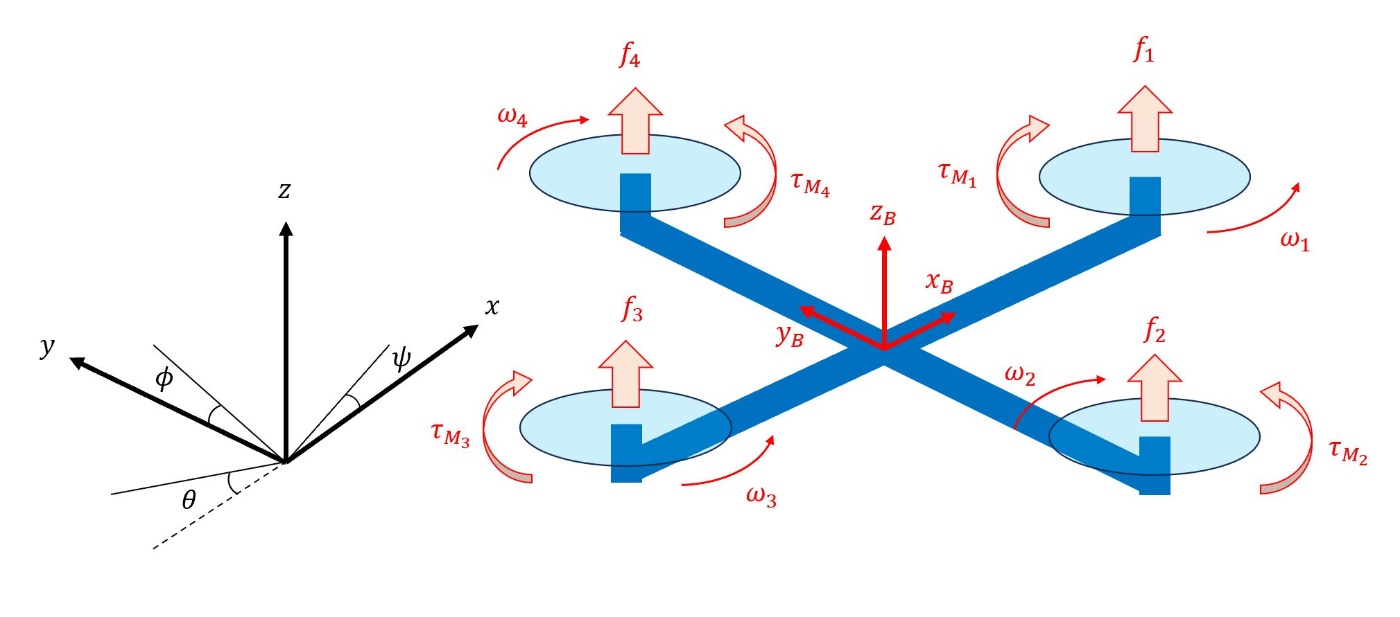
定数
\begin{align*}
&m : クアッドローターの質量 \\
&I_{b} : 剛体枠での慣性モーメント \\
&g : 重力加速度 \\
&b : プロペラ推力係数 \\
&d : プロペラトルク係数 \\
&l : 重心からプロペラまでの長さ \\
\end{align*}
変数
\begin{align*}
&\xi = \begin{bmatrix} x \\ y \\ z \end{bmatrix} : 位置\\
&\eta = \begin{bmatrix} \phi \\ \theta \\ \psi \end{bmatrix} : 「x-y-z」型のオイラー角\\
&q = \begin{bmatrix} \xi \\ \eta \end{bmatrix} : 一般化座標 \\
&\omega_{b} : 剛体枠での角速度ベクトル \\
&\omega_{*} : 各ローターの回転数 \quad (*=1,2,3,4) \\
&f_{*} : 各ローターの推力 \quad (*=1,2,3,4) \\
&\tau_{M*} : 各ローターのトルク \quad (*=1,2,3,4) \\
&u = \begin{bmatrix} u_1 \\ u_2 \\ u_3 \\ u_4 \end{bmatrix} : 制御入力\\
\end{align*}
関係式
\begin{align*}
&R = R_z(\psi)R_y(\theta)R_x(\phi) : 剛体枠から慣性枠への回転行列 \\
&\omega = W(\eta)\dot{\eta} : 角速度ベクトルとオイラー角の関係 \\
&W(\eta) =
\begin{bmatrix}
1 & 0 & -\sin(\theta) \\
0 & \cos(\phi) & \cos(\theta)\sin(\phi) \\
0 & -\sin(\phi) & \cos(\theta)\cos(\phi) \\
\end{bmatrix} \\
&J(\eta) = W(\eta)^TI_{b}W(\eta) : 一般化慣性項\\
&C(\eta,\dot{\eta}) = \dot{J(\eta)} - \frac{1}{2}\frac{\partial}{\partial \eta}(\dot{\eta}^TJ(\eta)) : コリオリ項\\
&u_{*} = \omega_{*}^2 \ge 0 \quad (*=1,2,3,4) \\
&f_{*} = b\omega_{*}^2 \quad (*=1,2,3,4) \\
&\tau_{M*} = d\omega_{*}^2 \quad (*=1,2,3,4) \\
&Q_{\xi} = R \begin{bmatrix} 0 \\ 0 \\ f_{1}+f_{2}+f_{3}+f_{4} \end{bmatrix} : 位置の一般化力\\
&Q_{\eta} = \begin{bmatrix} (f_3-f_1)l \\ (f_2-f_4)l \\ \tau_{M1}+\tau_{M2}+\tau_{M3}+\tau_{M4} \end{bmatrix} : 回転の一般化力\\
\end{align*}
オイラー・ラグランジュ法
\begin{align*}
&K_{trans} = \frac{1}{2}m\dot{\xi}^{T}\dot{\xi}: 並進運動による運動エネルギー \\
&K_{rot} = \frac{1}{2}\dot{\omega_{b}}^{T}I_{b}\dot{\omega_{b}} = \frac{1}{2}\dot{\eta}^TJ(\eta)\dot{\eta}: 回転運動による運動エネルギー \\
&U = mge^{T}_{z}\xi : 位置エネルギー \quad (e_zはz方向への単位ベクトル) \\
\end{align*}
ラグランジアンは
\begin{align*}
&\mathcal{L} = K_{trans} + K_{rot} - U \\
\end{align*}
で与えられるので、オイラー・ラグランジュの運動方程式によって、クアッドローターのダイナミクスは以下の通りに導出されます。
\begin{align*}
&m\ddot{\xi} + mge_z = Q_{\xi} \\
&J(\eta)\ddot{\eta} + C(\eta,\dot{\eta})\dot{\eta} = Q_{\eta} \\
\end{align*}
上記の方程式を\ddot{\xi},\ddot{\eta},uに関して整理すると、次の運動方程式が得られます。
\begin{align*}
\begin{bmatrix}
m & 0 \\ 0 & J(\eta)
\end{bmatrix}
\begin{bmatrix}
\ddot{\xi} \\ \ddot{\eta}
\end{bmatrix}
=
-\begin{bmatrix}
mge_z \\ C(\dot{\eta},\ddot{\eta})\dot{\eta}
\end{bmatrix}
+
\begin{bmatrix}
R\begin{bmatrix}
0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ b & b & b & b
\end{bmatrix} \\
\begin{bmatrix}
-bl & 0 & bl & 0 \\ 0 & bl & 0 & -bl \\ d & d & d & d
\end{bmatrix} \\
\end{bmatrix}u
\end{align*}
連続時間非線形MPCの定式化
現在の状態をx_0として、連続時間での最適化問題は以下のように定式化します。
\begin{gather}
&\min_{x(t),u(t)} J(x(t_f)) + \int_{t_0}^{t_f} L(\tau,x(\tau),u(\tau))d\tau \\
&{s.t.} \\
&\dot{x}(t) = f(t,x(t),u(t)) \\
&x_{min} \le x(t) \le x_{max} \\
&u_{min} \le u(t) \le u_{max} \\
&g(t,x(t),u(t)) \le 0 \\
&x(t_0)=x_0
&\end{gather}
このままではコンピューターで解くことが出来ないので、この問題を直行コロケーション法によって離散化(多項式で近似)します。
直行コロケーション法 (orthogonal collocation method)
直行コロケーション法(ガウス・ルジャンドル型選点法)とは、状態変数x(t)の軌道を区分的エルミート多項式p(t)で近似する際に、ガウス求積法的な意味において最適な点で拘束条件を満たすことによって、コスト関数とダイナミクスの拘束条件を精度良く近似する方法です。
今回はx(t)を5次の区分的エルミート多項式、u(t)を区分的1次多項式近似します。
準備
ガウス求積法より、任意の連続関数fに対して、
\begin{align*}
\int_{t_k}^{t_{k+1}}f(t)dt \fallingdotseq \sum_{i=1}^{3}w_{ci}f(t_{ci})
\end{align*}
となるようなw_{ci},x_{ci} (i=1,2,3)は、以下の通りです。
\begin{align*}
&w_{c1} = \frac{5}{9} \\
&w_{c2} = \frac{8}{9} \\
&w_{c3} = \frac{5}{9} \\
&t_{c1} = t_k + \frac{1-\sqrt{\frac{3}{5}}}{2}\Delta t \\
&t_{c2} = t_k + \frac{1}{2}\Delta t \\
&t_{c3} = t_k + \frac{1+\sqrt{\frac{3}{5}}}{2}\Delta t
\end{align*}
定式化
予測を行う区間[t_0,t_f]をN等分割して、各区間における区分的多項式を考えます。
ここで、以下のように各記号を定めます。
\begin{gather}
&T = t_f - t_0, \Delta t = T / N \\
&t_k = k\Delta t, x_k = x(t_k), u_k = u(t_k) \quad (k=0,...,N)\\
&f_k = f(t_k,x_k,u_k),g_k = g(t_k,x_k,u_k), L_k = L(t_k,x_k,u_k) \quad (k=0,...,N) \\
&t_{k_{c1}} = t_k + \frac{1-\sqrt{\frac{3}{5}}}{2}\Delta t, t_{k_{c2}} = t_k + \frac{1}{2}\Delta t, t_{k_{c3}} = t_k + \frac{1+\sqrt{\frac{3}{5}}}{2}\Delta t \quad (k=0,...,N) \\
&x_{k_{ci}} = x(t_{k_{ci}}), u_{k_{ci}} = u(t_{k_{ci}}) \quad (k=0,...,N, i=1,2,3) \\
&f_{k_{ci}} = f(t_{k_{ci}},x_{k_{ci}},u_{k_{ci}}), g_{k_{ci}} = g(t_{k_{ci}},x_{k_{ci}},u_{k_{ci}}) \quad (k=0,...,N, i=1,2,3)
\end{gather}
また上記の各変数を総称してt_{\ast},x_{\ast},u_{\ast}と表します。
まず区間[t_k,t_{k+1}]においてu(t)を1次の多項式q(t)を用いて近似を行います。
\begin{align*}
&q(t) = a + b \left(\frac{t-t_k}{t_{k+1}-t_k}\right)
\end{align*}
q(t)の2つの係数は区間の両端t_k,t_{k+1}において、x(t)の値が一致するように決めます。
\begin{align*}
&q(t_k) = u_k \\
&q(t_{k+1}) = u_{k+1} \\
\end{align*}
これを解くとq(t)は、
\begin{align*}
&q(t) = u_k(1-\left(\frac{t-t_k}{t_{k+1}-t_k}\right)) + u_{k+1}\left(\frac{t-t_k}{t_{k+1}-t_k}\right)
\end{align*}
と求まるので、このq(t)を改めて
\begin{align*}
&q(t:u_k,u_{k+1})
\end{align*}
と表します。
q(t:u_k,u_{k+1})を用いることで、コロケーションポイント上での値が次のように求まります。
\begin{align*}
&q(t_{k_{c1}}:x_k,x_{k+1}) = u_{k_{c1}} \\
&q(t_{k_{c2}}:x_k,x_{k+1}) = u_{k_{c2}} \\
&q(t_{k_{c3}}:x_k,x_{k+1}) = u_{k_{c3}} \\
\end{align*}
次に区間[t_k,t_{k+1}]においてx(t)を5次のエルミート多項式p(t)を用いて近似を行います。
\begin{align*}
&p(t) = a + b \left(\frac{t-t_k}{t_{k+1}-t_k}\right) + c \left( \frac{t-t_k}{t_{k+1}-t_k} \right)^2 + d \left( \frac{t-t_k}{t_{k+1}-t_k} \right)^3 + e \left( \frac{t-t_k}{t_{k+1}-t_k} \right)^4 + f \left( \frac{t-t_k}{t_{k+1}-t_k} \right)^5
\end{align*}
p(t)の6つの係数は区間の両端t_k,t_{k+1}とその中点t_{c2}において、x(t)と\dot{x}(t)の値が一致するように決めます。
\begin{align*}
&p(t_k) = x_k \\
&p(t_{k_{c2}}) = x_{k_{c2}} \\
&p(t_{k+1}) = x_{k+1} \\
&\dot{p}(t_k) = f_k \\
&\dot{p}(t_{k_{c2}}) = f_{k_{c2}} \\
&\dot{p}(t_{k+1}) = f_{k+1} \\
\end{align*}
上の式を整理すると、
\begin{align*}
\begin{bmatrix}
x_k & x_{k_{c2}} & x_{k+1} & f_k & f_{k_{c2}} & f_{k+1}
\end{bmatrix}
=
\begin{bmatrix}
a & b & c & d & e & f
\end{bmatrix}
\begin{bmatrix}
1 & 1 & 1 & 0 & 0 & 0 \\
0 & \frac{1}{2} & 1 & \frac{1}{\Delta t} & \frac{1}{\Delta t} & \frac{1}{\Delta t} \\
0 & \frac{1}{2^2} & 1 & 0 & \frac{1}{2}\frac{2}{\Delta t} & \frac{2}{\Delta t} \\
0 & \frac{1}{2^3} & 1 & 0 & \frac{1}{2^2}\frac{3}{\Delta t} & \frac{3}{\Delta t} \\
0 & \frac{1}{2^4} & 1 & 0 & \frac{1}{2^3}\frac{4}{\Delta t} & \frac{4}{\Delta t} \\
0 & \frac{1}{2^5} & 1 & 0 & \frac{1}{2^4}\frac{5}{\Delta t} & \frac{5}{\Delta t} \\
\end{bmatrix}
\end{align*}
となるので、これより解くことにより、p(t)の係数をx_k , x_{k_{c2}} , x_{k+1} , f_k , f_{k_{c2}} , f_{k+1}で記述することができるので、p(t)を改めて、
\begin{align*}
&p(t) = p(t:x_k,x_{k_{c2}},x_{k+1},f_k,f_{k_{c2}},f_{k+1})
\end{align*}
と表します。
これにより、p(t:x_k,x_{k_{c2}},x_{k+1},f_k,f_{k_{c2}},f_{k+1})が可能な限り\dot{x}(t)=f(t,x(t),u(t))を満たすようにすることから、コロケーションポイントでの等式制約条件が次のように導かれます。
\begin{align*}
&p(t_{k_{c1}}:x_k,x_{k_{c2}},x_{k+1},f_k,f_{k_{c2}},f_{k+1}) = x_{k_{c1}} \\
&p(t_{k_{c3}}:x_k,x_{k_{c2}},x_{k+1},f_k,f_{k_{c2}},f_{k+1}) = x_{k_{c3}} \\
&\dot{p}(t_{k_{c1}}:x_k,x_{k_{c2}},x_{k+1},f_k,f_{k_{c2}},f_{k+1}) = f_{k_{c1}} \\
&\dot{p}(t_{k_{c3}}:x_k,x_{k_{c2}},x_{k+1},f_k,f_{k_{c2}},f_{k+1}) = f_{k_{c3}} \\
\end{align*}
以上より、元の連続時間の最適化問題は次のように離散化することが出来ます。
\begin{gather}
\min_{x_{*},u_{*}} J(x_{N}) + \sum_{k=0}^{N}L_k \\
s.t \\
p(t_{k_{c1}}:x_k,x_{k_{c2}},x_{k+1},f_k,f_{k_{c2}},f_{k+1}) = x_{k_{c1}} \\
p(t_{k_{c3}}:x_k,x_{k_{c2}},x_{k+1},f_k,f_{k_{c2}},f_{k+1}) = x_{k_{c3}} \\
\dot{p}(t_{k_{c1}}:x_k,x_{k_{c2}},x_{k+1},f_k,f_{k_{c2}},f_{k+1}) = f_{k_{c1}} \\
\dot{p}(t_{k_{c3}}:x_k,x_{k_{c2}},x_{k+1},f_k,f_{k_{c2}},f_{k+1}) = f_{k_{c3}} \\
q(t_{k_{c1}}:x_k,x_{k+1}) = u_{k_{c1}} \\
q(t_{k_{c2}}:x_k,x_{k+1}) = u_{k_{c2}} \\
q(t_{k_{c3}}:x_k,x_{k+1}) = u_{k_{c3}} \\
x_{min} \le x_{*} \le x_{max} \\
u_{min} \le u_{*} \le u_{max} \\
g_* \le 0 \\
x_0 = x_0 \quad (初期状態) \\
(k=0,...,N) \\
\end{gather}


Discussion