ADMMによる画像圧縮センシング
圧縮センシングとは?
圧縮センシングは少ない観測データから元の信号を復元する方法で、名前の由来は観測(センシング)を間引く(圧縮する)ことから来ています。 MRIを中心に医療技術や宇宙探査など様々な分野で用いられており、この技術はとりわけ1回あたりの観測コストが高いようなタスク、 あるいは観測回数を減らすベネフィットが大きいタスクなどに対してその真価を発揮します。
欠損した信号の復元が可能な理由は、観測される信号には事前にある程度パターンが予測できる場合があるからです。 すなわち、画像には「画像らしさ」が、音声には「音声らしさ」があり、欠損した情報を補うことができるということが知られています。 これは人間を含めた生物の脳が自然に行っていることであり、それを数理的なアルゴリズムに置き換えたものが圧縮センシングです。
画像の持つ性質とスパース性
画像が普遍的に持っている性質として以下のようなものが知られています。
- ある画素の隣の画素は似ていることが多い。つまり画素値の低周波成分が強く、画素間の局所相関が高い。
- 画素値が急に変わる部分、つまりエッジのような部分は1次元的に連続してつながっていることが多い。
- 画素値の変化は写っている物体それぞれの場所とスケールに応じている。
これらの性質は画像の「全変動」と「ウェーブレット変換後の係数」に対するスパース性として現れることが知られています。
最適化問題としての圧縮センシング
圧縮センシングを使えば欠損ありの画像に対して、再構成画像を生成することができます。 この際、再構成画像は「観測された画素値をなるべく再現しながら同時に先ほどのスパース性を満たす」ように選ばれます。
これはL1正則化を用いた最適化問題として定式化することができます。
観測画素を一次元に並べ替えたものを
再構成画像と観測画像の間をつなげる写像(サンプリング行列)を
とします。
拡張ラグランジュ関数
これに補助変数
zをまとめて
と書くと、拡張ラグランジュ関数は
と与えられます。
ADMMによる最適化
更新の式は
で与えられます。
したがって
xの更新
二次関数の最小化なので解析的に解けますが、行列Gのサイズは非常に大きくなるため直接Gを用いない形式が望ましいです。そこで、例えば共役勾配法を用いれば任意のxに対しGxを与える関数が得られれば行列計算を回避して解くことが可能になります。
したがってウェーブレット変換とSobelフィルタ、Gaborフィルタを用いて実装すれば、メモリと計算量をかなり節約できます。
xの損失関数を
より、勾配とヘッセ行列は
となります。ここでPはサンプリング行列であり、インデックスなので、観測値
#obs_image:入力画像
obs = obs_image.reshape(-1)
obs_mask = ( obs != 0 )
#初期値
x = np.copy(np.zeros(obs.shape))
z_W = pywt.wavedec2(x.reshape(256,256),'haar')
z_W = pywt.coeffs_to_array(z_W)[0].reshape(-1)
z = z_W
v_W = np.zeros(z_W.shape)
v = v_W
#観測値
y = obs[obs_mask]
#サンプリング行列の計算
PTy = np.zeros(x.shape)
PTy[obs_mask] = y
Px = x[obs_mask]
PTPx = np.zeros(x.shape)
PTPx[obs_mask] = x[obs_mask]
一方でGは次のように計算されます。
(ただし
微分
zの更新
vの更新
ソースコード全体
import numpy as np
import cv2
from PIL import Image
from IPython.core.display import display
import pywt
from scipy import optimize
def draw_image_via_PIL(image):
buff = np.array(image,dtype=np.float64)
# buff = 255 * image
#buff = (buff - buff.min()) / (buff.max() - buff.min())
buff = np.array(buff , dtype=np.uint8)
display(Image.fromarray(buff))
def calc_Dx(image,reverse=False):
result = np.zeros(image.shape)
if not reverse:
result[:, 1:] = image[:, 1:]
result[:, 1:] -= image[:,:-1]
elif reverse:
result[:, :-1] = image[:, :-1]
result[:, :-1] -= image[:,1:]
return result
def calc_Dy(image,reverse=False):
result = np.zeros(image.shape)
if not reverse:
result[1:, :] = image[1:, :]
result[1:, :] -= image[:-1, :]
elif reverse:
result[:-1, :] = image[:-1, :]
result[:-1, :] -= image[1:, :]
return result
#画像をリサイズ
imsize = 256
image = cv2.resize(pywt.data.camera(),dsize=(imsize,imsize),interpolation=cv2.INTER_AREA) / 255
#間引き
obs_image = np.copy(image)
obs_image[np.random.randint(0,imsize,int(imsize*imsize*0.9)),
np.random.randint(0,imsize,int(imsize*imsize*0.9))] = 0
obs = obs_image.reshape(-1)
obs_mask = obs != 0
gamma = 0.002
alpha_W = 0.001
alpha_TV = 0.001
# wavelet = 'db2'
# wavelet = 'db20'
wavelet = 'bior6.8'
# wavelet = 'rbio6.8'
_, pywt_slices = pywt.coeffs_to_array(pywt.wavedec2(np.zeros((imsize, imsize)),wavelet))
z_W_shape = _.shape
#ADMMの中でxを最適化する時に使う共役勾配法のための関数l, grad_lx, Hx_p
#損失関数lx(x)
def lx(x):
x_2d = x.reshape(imsize, imsize)
Px = x[obs_mask]
f1 = np.sum( ( Px - y) ** 2)
GWx = pywt.coeffs_to_array(pywt.wavedec2(x_2d,wavelet))[0]
GWx = alpha_W * GWx.reshape(-1)
f2_GW = np.sum( ( GWx - z_W + v_W ) ** 2)
GDx = alpha_TV * calc_Dx(x_2d).reshape(-1)
f2_GDx = np.sum((GDx - z_Dx + v_Dx) ** 2)
GDy = alpha_TV * calc_Dy(x_2d).reshape(-1)
f2_GDy = np.sum((GDy - z_Dy + v_Dy) ** 2)
return f1 / 2 + ( f2_GW + f2_GDx + f2_GDy ) / ( 2 * gamma )
#lxの勾配
def grad_lx(x):
x_2d = x.reshape(imsize, imsize)
PTPx = np.zeros(x.shape)
PTPx[obs_mask] = x[obs_mask]
GWTGWx = alpha_W ** 2 * np.copy(x) #waveletのみ
GDxTGDxx = alpha_TV ** 2 * calc_Dx(calc_Dx(x_2d),reverse=True).reshape(-1)
GDyTGDyx = alpha_TV ** 2 * calc_Dy(calc_Dy(x_2d),reverse=True).reshape(-1)
GTGx = GWTGWx + GDxTGDxx + GDyTGDyx
PTy = np.zeros(x.shape)
PTy[obs_mask] = y
z_v_W = z_W - v_W
GWTz_v_W = pywt.array_to_coeffs(z_v_W.reshape(z_W_shape), pywt_slices,"wavedec2")
GWTz_v_W = pywt.waverec2(GWTz_v_W,wavelet)
GWTz_v_W = alpha_W * GWTz_v_W.reshape(-1)
z_v_Dx = z_Dx - v_Dx
GDxTz_v_Dx = calc_Dx(z_v_Dx.reshape(imsize, imsize), reverse=True)
GDxTz_v_Dx = alpha_TV * GDxTz_v_Dx.reshape(-1)
z_v_Dy = z_Dy - v_Dy
GDyTz_v_Dy = calc_Dy(z_v_Dy.reshape(imsize, imsize), reverse=True).reshape(-1)
GDyTz_v_Dy = alpha_TV * GDyTz_v_Dy.reshape(-1)
GTz_v = GWTz_v_W + GDxTz_v_Dx + GDyTz_v_Dy
return PTPx + (GTGx / gamma) - PTy - GTz_v / gamma
#lxのヘシアンと任意のベクトルpの積
def Hx_p(x, p):
p_2d = p.reshape(imsize, imsize)
PTPp = np.zeros(x.shape)
PTPp[obs_mask] = p[obs_mask]
GWTGWp = alpha_W ** 2 * np.copy(p)
GDxTGDxp = alpha_TV ** 2 * calc_Dx(calc_Dx(p_2d),reverse=True).reshape(-1)
GDyTGDyp = alpha_TV ** 2 * calc_Dy(calc_Dy(p_2d),reverse=True).reshape(-1)
GTGp = GWTGWp + GDxTGDxp + GDyTGDyp
return PTPp + GTGp / gamma
gif_images = []
#初期値
# x = np.zeros(obs.shape)
x = np.copy(obs)
# z_W = pywt.wavedec2(x.reshape(256,256),wavelet)
# z_W = pywt.coeffs_to_array(z_W)[0].reshape(-1)
# z_Dx = calc_Dx(x.reshape(imsize,imsize)).reshape(-1)
# z_Dy = calc_Dy(x.reshape(imsize,imsize)).reshape(-1)
z_W = np.zeros(z_W_shape).reshape(-1)
z_Dx = np.zeros(imsize*imsize)
z_Dy = np.zeros(imsize*imsize)
v_W = np.zeros(z_W.shape)
v_Dx = np.zeros(imsize*imsize)
v_Dy = np.zeros(imsize*imsize)
#観測値
y = obs[obs_mask]
for i in range(101):
gif_images.append(Image.fromarray(np.array(x.reshape(imsize,imsize)*255, dtype=np.uint8 )))
if i%10 == 0:
print(i)
# draw_image_via_PIL(x.reshape(imsize,imsize)*255)
#xの更新
res = optimize.minimize(lx, x, method='Newton-CG',
jac=grad_lx, hessp=Hx_p,
options={'xtol': 1e-8, 'disp': False})
# res = optimize.minimize(lx, x, method='L-BFGS-B',
# jac=grad_lx,
# options={'gtol': 1e-8, 'disp': True})
x = res.x
#zの更新
GWx = alpha_W * pywt.coeffs_to_array(pywt.wavedec2(x.reshape(imsize,imsize),wavelet))[0].reshape(-1)
z_W = pywt.threshold(GWx + v_W, gamma, 'soft')
GDxx = alpha_TV * calc_Dx(x.reshape(imsize,imsize)).reshape(-1)
z_Dx = pywt.threshold(GDxx + v_Dx, gamma, 'soft')
GDyx = alpha_TV * calc_Dy(x.reshape(imsize, imsize)).reshape(-1)
z_Dy = pywt.threshold(GDyx + v_Dy, gamma, 'soft')
#vの更新
v_W = v_W + GWx - z_W
v_Dx = v_Dx + GDxx - z_Dx
v_Dy = v_Dy + GDyx - z_Dy
if alpha_W == 0:
gif_images[0].save('TV.gif'.format(wavelet), save_all=True, append_images=gif_images[1::2],loop=0)
elif alpha_TV == 0:
gif_images[0].save('{}.gif'.format(wavelet), save_all=True, append_images=gif_images[1::2],loop=0)
else:
gif_images[0].save('{}_TV.gif'.format(wavelet), save_all=True, append_images=gif_images[1::2],loop=0)
print("end")
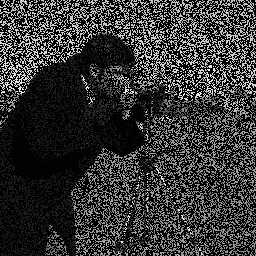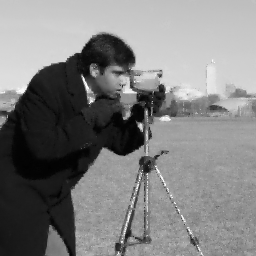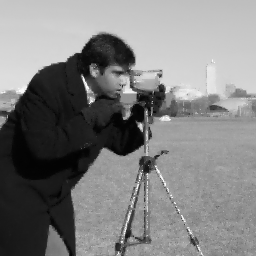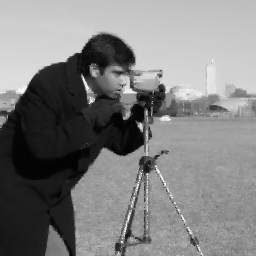

Discussion