🎯
円内部のランダムな3点がつくる三角形面積の期待値【Expected area of random triangle in a circle

2025/05/02に公開
 はじめに前に自作した「円周上のランダムな3点がつくる三角形面積の期待値」が無事に解けたので、1次元とくれば次は2次元、ということで、タイトルの「円内部の～」に取り組んでみることにした──というのが2023年のおはなし。1年半経った今も、ネットで調べても日本語/英語ともに満足な回答が出てこないので、思い切って成果を記事にしてみることにした。タイトルに英語をくっつけているのは、運が良ければお困りの海外ニキにも届くかも？と思ってのこと。解くにあたって助けてくれた見知らぬ海外ニキ（Henry）、ありがとう！
!この問題を解くためには重積分と極座標の知識が必要です、たぶん。
さて、ここからはお気持ち数学（Feeling math）領域を展開する。お気持ち数学（造語）とは、「ああ、確かにそれならそうなりそうだ」という感覚を重視し、数学的厳密性に対しては「こまけぇこたぁいいんだよ！！」を決め込んで行う数学のこと。工学系が得意とする。私はお気持ち数学記事しか書けかない。

 悩んだ経緯と正しい答え■もし自力で解けそうであれば、ここで立ち止まって一度解いてみてほしい。
自分がはじめに出した答えはこれ↓だった（円の半径を R とした）。正しい答えはこの節の最下部。
はじめに出した答え（これは間違っている）E[S]=\frac{2}{3\pi}R^2\simeq 0.21221R^2
（同じ答えになってしまった人はおそらく同じポイントで嵌まっている）
私は、得られた答えが合っているか確かめようと思い、みんな大好きモンテカルロ法でランダム三角形の面積の平均を出してみることにした。

Pythonのコードと実行例を置いておく（円の半径は1としている）。
Pythonのコードと実行例モンテカルロ法で平均値を求めるコード
import numpy as np

rand_gen = np.random.default_rng()
print("How many triangles do you generate to calculate average of area?:")
num = int(input())
area_triangle = []
for i in range(num):
    points = []
    for point in range(3):
        while True:
            x = rand_gen.uniform(-1.0, 1.0)
            y = rand_gen.uniform(-1.0, 1.0)
            if x**2 + y**2 <= 1.0:
                points.append([x, y])
                break
    v1 = [points[1][0] - points[0][0], points[1][1] - points[0][1]]
    v2 = [points[2][0] - points[0][0], points[2][1] - points[0][1]]
    #
    area_triangle.append((1/2)*np.abs(v1[0]*v2[1] - v1[1]*v2[0]))
print("average of area: " + str(np.mean(area_triangle)))
実行例
How many triangles do you generate to calculate average of area?:
10000000
average of area:0.2321864169770789
自分が出した答えとわずかにズレている……！　初めはモンテカルロ法の精度を疑ったが、平均する数を増やしてみて、さすがに10,000,000個の平均が2%もズレるわけがない！ということで見直してみたところ、自分の考え方ではわずかに負の面積を勘定に入れてしまうということが分かった。円周上の3点の場合と違って、3点 P_1(r_1,\phi_1),P_2(r_2,\phi_2),P_3(r_3,\phi_3) が 0=\phi_1<\phi_2<\phi_3<2\pi であっても、\frac{1}{2}(r_1r_2\sin(\phi_2 -\phi_1)+r_2r_3\sin(\phi_3 -\phi_2)+r_3r_1\sin(\phi_1 -\phi_3)) が必ず正とは限らないのだ。つまるところ、角度が \phi_1,\phi_2,\phi_3 で反時計回りになっていても P_1,P_2,P_3 が平面上で時計回りに並んでしまうパターンが存在する、という欠陥を抱えていたわけだ。

 で、正しい答えはこちら正しい答えE[S]=\frac{35}{48\pi}R^2\simeq 0.23210R^2
これを今から求めていく。

 証明・解説はじめに、ここで紹介する解き方の全体的な流れを説明する。
円（半径： R）の内部からランダムに選ばれた3点のうち、最も円の外側に位置するものを p_0 とし、円の中心からの距離を q とする。
半径 q、微小幅 dq の円環領域内に最遠点 p_0 が来る確率 dP を dq を使って表す。
半径 q の円の内部に作られる任意の図形（円と同じスケールで拡大縮小されるものとする）の面積を kq^2 とする。k は図形によって変わる比例定数で、例えば半径 q の円そのものなら k=\pi。（実際には、図形は「円の内部」でなくてもよい）

半径 q の円周上に1点が固定されたので、「半径 R の円内部から3点を選ぶ」問題が「半径 q$ の円内部から2点を選ぶ」問題に帰着される。「半径 q の円周上から1点、内部から2点をランダムに選んで作られる、三角形の面積の期待値 E[S_q]\ (=E[kq^2])」を式で表す。
「2点ランダム下での三角形の面積の期待値 E[kq^2]」、「その状況になる確率 dP」が決まったので、その積を 0\le q<R で積分することで、「円周上のランダムな3点がつくる三角形の面積の期待値」が求まる。
図で書くとこんな感じ。



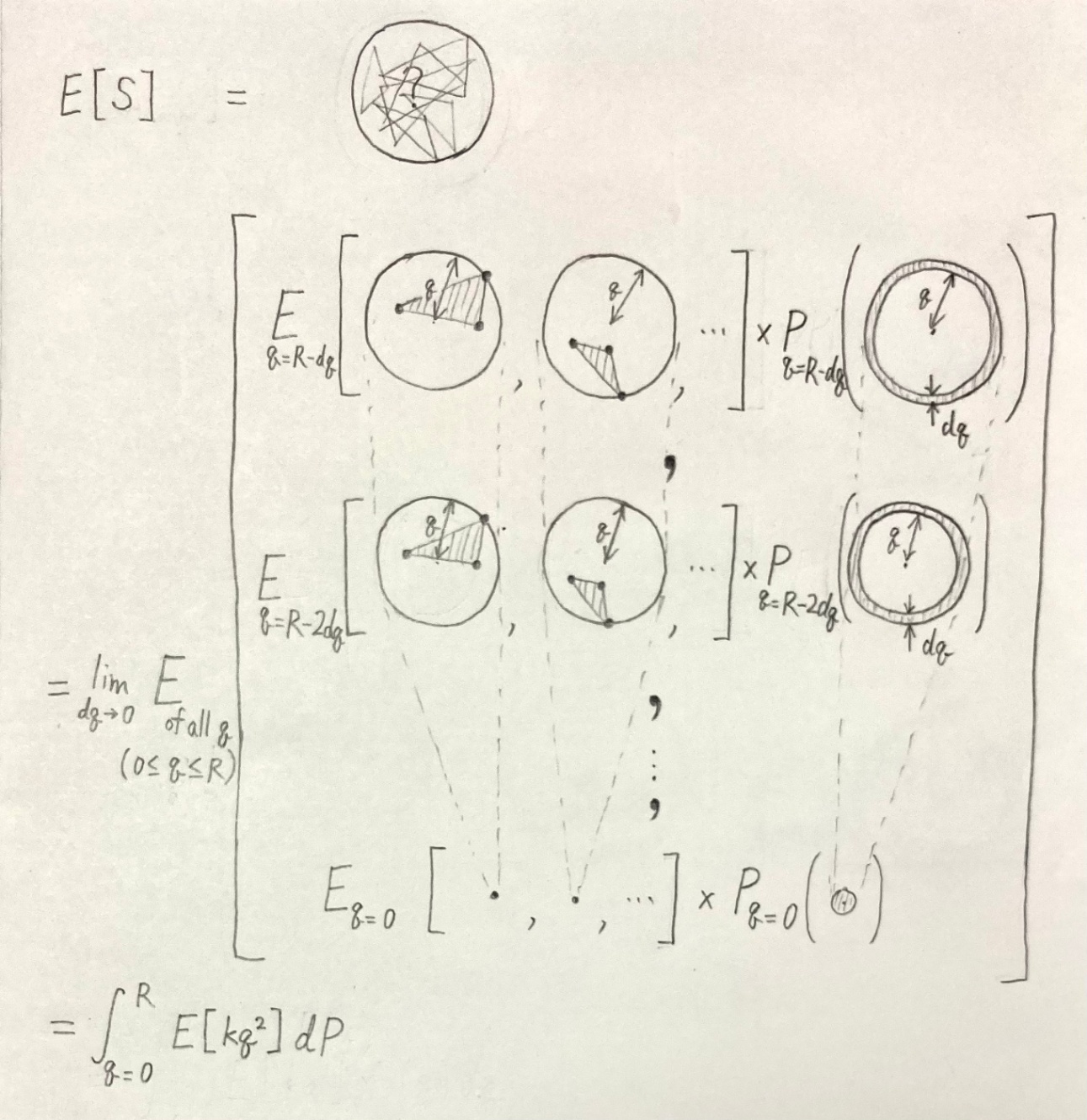
思ったより分かりやすくならなかったな……
ここからは実際に式を立ててこねていく。

半径 q、微小幅 dq の円環領域内に最遠点 p_0 が来る確率 dP：

　円全体の面積 \pi R^2 において、p_0 が微小幅円環の面積 2\pi q\times dq から選ばれ、かつ残りの2点は半径 q の内側面積 \pi q^2 から選ばれ、さらに3点のうちどの点も最遠点になりえるので、この確率はこう書ける。

\begin{split}
dP&=\frac{2\pi q\times dq}{\pi R^2}\frac{\pi q^2}{\pi R^2}\frac{\pi q^2}{\pi R^2}\times 3\\
&=\frac{6}{R^6}q^5dq
\end{split}

半径 q の円周上から1点、内部から2点をランダムに選んで作られる、三角形の面積の期待値 E[kq^2]：

　これには少し工夫が必要。平面上で常に3点が反時計回り（または時計回り）に並んでいないと、式から絶対値が外せず大変なことになる（この工夫のためにわざわざ最遠点を円の端に固定した）。

　そのため、まず（p_0 は円周上のどこにあっても結果は同じになるので）p_0 のある場所を新たに原点とすることを考える。このとき円を、原点を通り、第1象限と第2象限にまたがるように設定する。すると、円の範囲は D_{\mathrm{circle}}(q):\ \{0\le r<2q\sin \phi,\ 0\le \phi <\pi \} と表すことができる。

※以下の図を参照
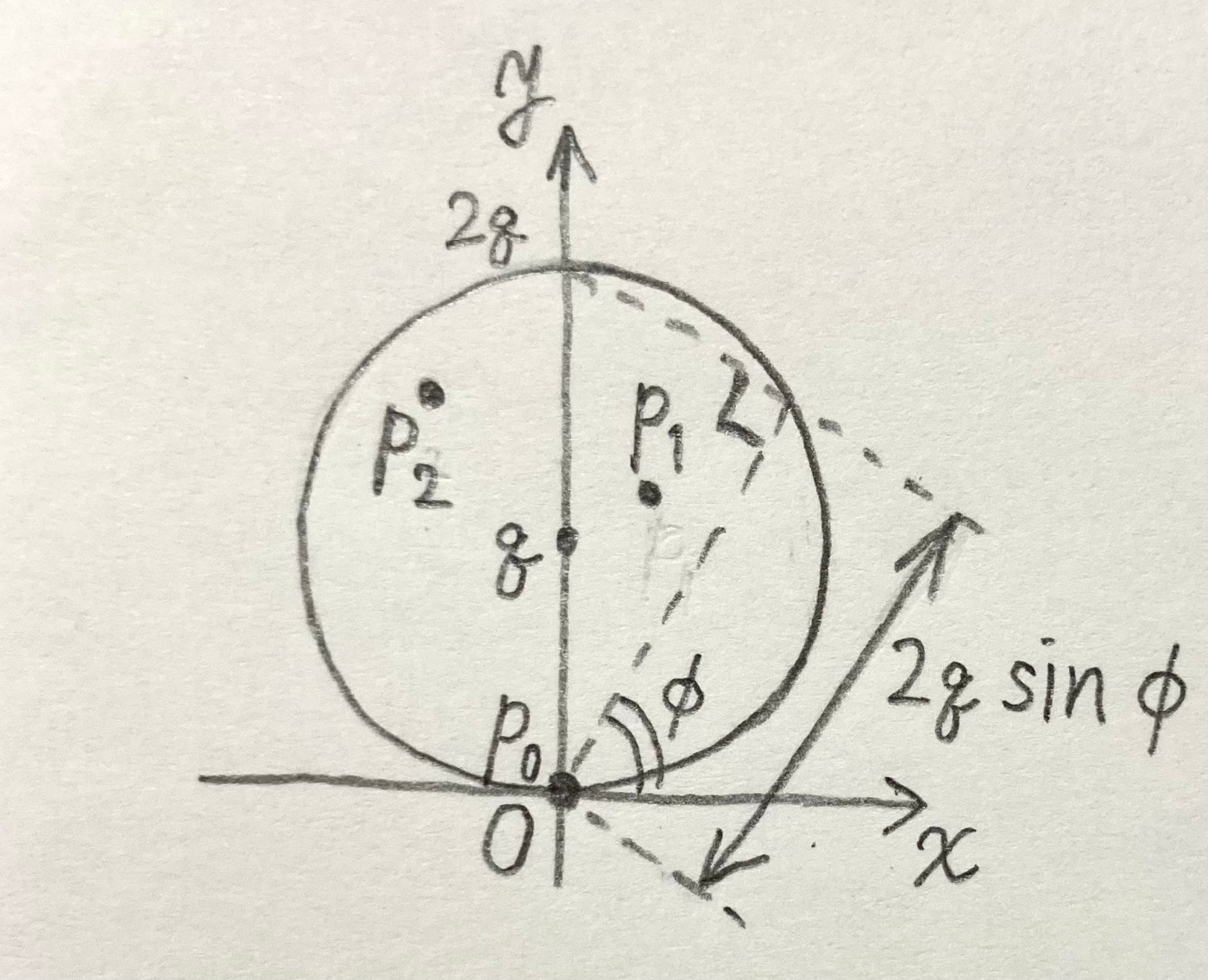
固定されていない2点を p_1(r_1,\phi_1),p_2(r_2,\phi_2) とし、\phi_1<\phi_2 の条件をつけることで、三角形 p_0p_1p_2 の面積 S_q は、絶対値を使わずに \frac{1}{2}r_1r_2\sin(\phi_2-\phi_1) と表せる。これを p_1,p_2 それぞれについて D_{\mathrm{circle}}(q) 全域で積分し、D_{\mathrm{circle}}(q) 全域の面積 \pi q^2 で割り、最後に \phi_1 と \phi_2 が逆である場合を考慮した 2 を掛ければ、1点固定時の面積期待値 E[kq^2] が求まる。

※　\squareで囲った部分は \phi_1 と \phi_2 の積分順序の交換を使っているので注意。

\begin{split}
E[kq^2]&=\frac{1}{(\pi q^2)^2}\int_{p_1\in D_{\mathrm{circle}}}\int_{p_2\in D_{\mathrm{circle}}}
S_q(p_1,p_2)\ dp_1dp_2\ \times 2

\\
&=\frac{1}{\pi^2 q^4}\int_{\phi_2=0}^\pi\int_{\phi_1=0}^{\phi_2}\int_{r_2=0}^{2q\sin\phi_2}\int_{r_1=0}^{2q\sin\phi_1}
\frac{1}{2}r_1r_2\sin(\phi_2-\phi_1)\ r_1dr_1d\phi_1\ r_2dr_2d\phi_2\ \times 2

\\
&=\frac{1}{\pi^2 q^4}\int_{\phi_2=0}^\pi\int_{\phi_1=0}^{\phi_2}\frac{1}{3^2}(2q\sin\phi_1)^3 (2q\sin\phi_2)^3 \sin(\phi_2-\phi_1) d\phi_1d\phi_2

\\
&=\frac{1}{\pi^2 q^4}\int_{\phi_2=0}^\pi\int_{\phi_1=0}^{\phi_2} \frac{64}{9}q^6
\sin^3\phi_1 \sin^3\phi_2\ (\sin\phi_2\cos\phi_1 - \cos\phi_2\sin\phi_1) d\phi_1d\phi_2

\\
&=\frac{64q^2}{9\pi^2}\left[
\int_0^\pi\sin^4\phi_2\left(\int_0^{\phi_2} \sin^3\phi_1 \cos\phi_1 d\phi_1\right)d\phi_2
- \boxed{\int_0^{\pi}} \sin^4\phi_1 \left(\boxed{\int_{\phi_1}^\pi}\sin^3\phi_2\cos\phi_2 \boxed{d\phi_2}\right)\boxed{d\phi_1}
\right]

\\
&=\frac{64q^2}{9\pi^2}\left[
\int_0^\pi\sin^4\phi_2\left[\frac{1}{4}\sin^4\phi_1\right]_0^{\phi_2}d\phi_2
- \int_0^\pi \sin^4\phi_1 \left[-\frac{1}{4}\sin^4\phi_2\right]_{\phi_1}^\pi d\phi_1
\right]
\\
&=\frac{64q^2}{9\pi^2}\cdot\frac{1}{4}\left(
\int_0^\pi\sin^8\phi_2d\phi_2
+ \int_0^\pi \sin^8\phi_1 d\phi_1
\right)
\\
&=\frac{64q^2}{9\pi^2}\cdot\frac{1}{4}\left(
2\int_0^{\frac{\pi}{2}}\sin^8\phi_2d\phi_2
+ 2\int_0^{\frac{\pi}{2}} \sin^8\phi_1 d\phi_1
\right)

\\
&=\frac{64q^2}{9\pi^2}\cdot\frac{1}{4}\cdot
2\left(\frac{1\cdot 3\cdot 5\cdot 7}{2\cdot 4\cdot 6\cdot 8}\cdot\frac{\pi}{2}
+\frac{1\cdot 3\cdot 5\cdot 7}{2\cdot 4\cdot 6\cdot 8}\cdot\frac{\pi}{2}\right)
\ \ \mathrm{(← Wallis'\ integrals)}

\\
&=\frac{64q^2}{9\pi^2}\cdot\frac{1}{4}\cdot
2\left(\frac{35\pi}{256}+\frac{35\pi}{256}\right)

\\
&=\frac{35}{36\pi}q^2
\end{split}
そして最後に、E[kq^2] と dP の積を 0\le q<R で積分して得られる、円周上のランダムな3点がつくる三角形の面積の期待値 E[S]：

\begin{split}
E[S]&=\int_{q=0}^R E[kq^2]dP

\\
&=\int_0^R \frac{35}{36\pi}q^2\ \frac{6}{R^6}q^5dq

\\
&=\frac{35}{36\pi}\cdot \frac{6}{R^6}\cdot \frac{1}{8}R^8

\\
&=\frac{35}{48\pi}R^2
\end{split}

 さいごに普通に気が狂う！　こんなん自分一人で思いつけるわけない！！

あ、もっと🌹elegant✨️な解き方あるよ～って人はぜひ教えてください（私に理解できるか分かりませんが）。
てかはじめてZennで書いてみたけど使い心地最高じゃんね

技術寄りだから数学記事の扱いがどうなのか知らないけど

ルビ振りと中央寄せが実装されたらさらに良い
はじめに

悩んだ経緯と正しい答え

で、正しい答えはこちら

証明・解説

さいごに

Discussion
