概要
画像の品質を測定する手法BRISQUEを提案している論文。
BRISQUEはOpenCVでも実装されているような画像品質測定の標準的な手法のひとつで、DCTやウェーブレットによる別空間への変換を行わずに計算できることもあり、高速かつ高精度な品質測定手法である。
BRISQUEでは、歪み(画質の劣化)の大きさや種類を分類できる特徴量を提案し、それを用いたSVMモデルを訓練する。
書誌情報
- Mittal, Anish, Anush Krishna Moorthy, and Alan Conrad Bovik. "No-reference image quality assessment in the spatial domain." IEEE Transactions on image processing 21.12 (2012): 4695-4708.
ポイント
BRISQUEが使用するのは、以下に示す18次元の特徴量である。最初の2つはMSCNと呼ばれるウィンドウを用いて局所的に正規化された輝度の分布を、一般化ガウス分布(GGM)に当てはめたときのパラメータである。
残りの16個は、MSCNの水平、垂直、対角方向(右上方向と右下方向)の相関(ペアワイズ積)の分布を非対称一般化ガウス分布(AGGM)と捉えた時のパラメータである。各ペアワイズ積ごとに4次元の特徴量であるため、16次元となる。
さらに、これらの特徴量をオリジナルの解像度と半分の解像度とで抽出し、全体としては36次元の特徴量としている。
MSCN
MSCN(mean subtracted contrast normalized)は、以下の式で求められる\hat{I}の分布である。MSCNは文字通り、平均を差し引いて標準偏差で割ることでコントラストを正規化したものである。C=1はゼロ割回避のための定数である。
\hat{I}(i, j)=\frac{I(i, j)-\mu(i, j)}{\sigma(i, j)+C}
MSCNは(2K+1)\times(2L+1)のサイズのウィンドウによって区切られた範囲で算出される\mu(i, j), \sigma(i, j)を使用して求められる。ウィンドウw_{k,l}は、ガウシアンフィルターである。ウィンドウの大きさを決めるK, Lは、K=L=3が使用される。
\begin{aligned} &\mu(i, j)=\sum_{k=-K}^{K} \sum_{l=-L}^{L} w_{k, l} I_{k, l}(i, j) \\ &\sigma(i, j)=\sqrt{\sum_{k=-K}^{K} \sum_{l=-L}^{L} w_{k, l}\left(I_{k, l}(i, j)-\mu(i, j)\right)^{2}} \end{aligned}
w=\left\{w_{k, l} \mid k=-K, \ldots, K, l=-L, \ldots L\right\}
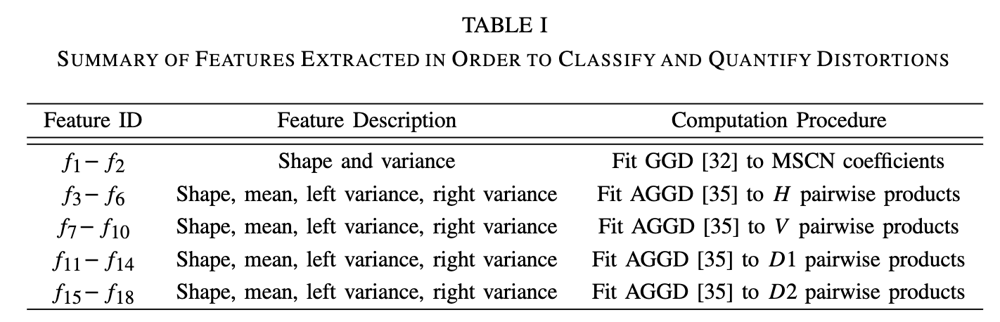
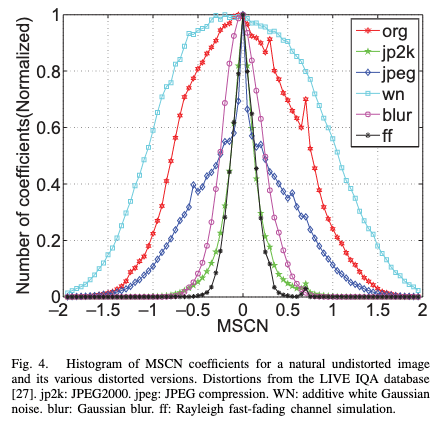
下図に示すように、MSCNは自然な画像であればガウス分布に近くなる。しかし、人工的な画像(CGやノイズの乗った画像)ではガウス分布からかけ離れた形になる。
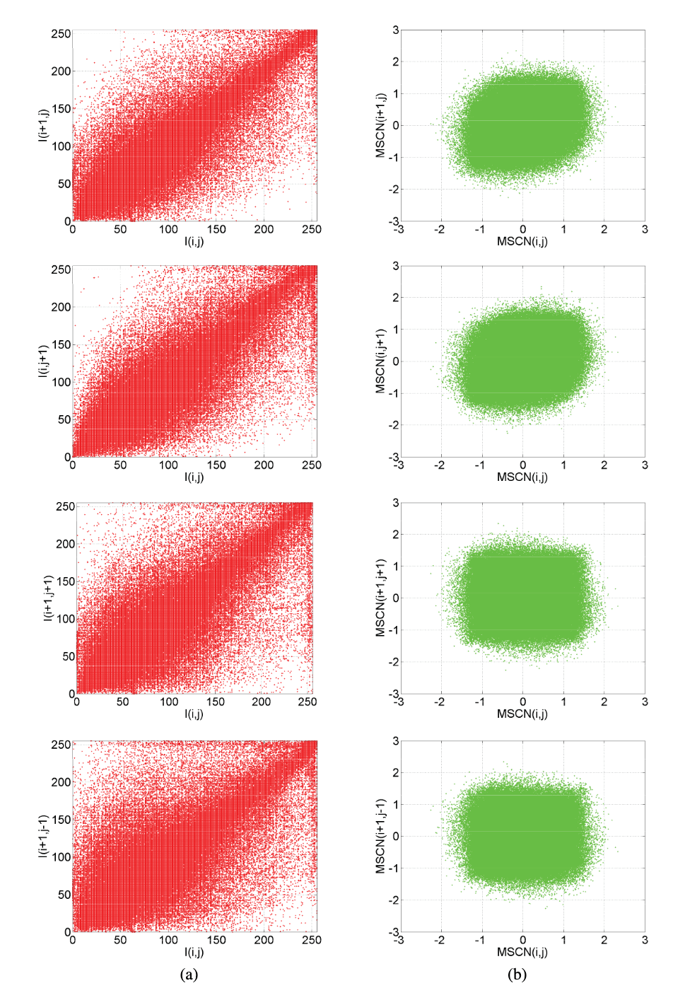
下図は、自然な画像における輝度IとMSCNについて、座標(i, j)と右(i+1,j)・下(i,j+1)・右下(i+1,j+1)・右上(i+1,j-1)との相関を表す散布図である。輝度は当然局所的な相関が高いので対角線上に多くの点が分布しているが、MSCNは局所的な相関がうまく取り除けていることがわかる。
歪みを定量的に表現するために、MSCNの分布を一般化ガウス分布(GGM)と捉え、そのパラメータを特徴量とすることを考える。一般化ガウス分布はガウス分布とラプラス分布を一般化したもので、平均が0であるという前提を置くと、shapeパラメータ\alphaと分散\sigma^2を用いて、以下のように表現できる。\Gamma(\cdot)はガンマ関数である。
f\left(x ; \alpha, \sigma^{2}\right)=\frac{\alpha}{2 \beta \Gamma(1 / \alpha)} \exp \left(-\left(\frac{|x|}{\beta}\right)^{\alpha}\right)
\beta=\sigma \sqrt{\frac{\Gamma(1 / \alpha)}{\Gamma(3 / \alpha)}}
このようなshapeパラメータ\alphaと分散\sigma^2を特徴量として使用できる。
ペアワイズ積
先に示した、4つの方向(右、下、右下、右上)のMSCN間の積H, V, D1, D2をペアワイズ積と呼ぶことにする。
\begin{aligned} H(i, j) &=\hat{I}(i, j) \hat{I}(i, j+1) \\ V(i, j) &=\hat{I}(i, j) \hat{I}(i+1, j) \\ D 1(i, j) &=\hat{I}(i, j) \hat{I}(i+1, j+1) \\ D 2(i, j) &=\hat{I}(i, j) \hat{I}(i+1, j-1) \end{aligned}
一般的な画像のテクスチャにおけるペアワイズ積は、歪んだ裾の重い分布に従うことが知られており、以下に示すような非対称一般化ガウス分布(AGGM)に当てはめることが適切であるということが既存の研究によって知られている。なお、ここで最頻値は0であるという前提を置いている。
f\left(x ; \nu, \sigma_{l}^{2}, \sigma_{r}^{2}\right)= \begin{cases}\frac{\nu}{\left(\beta_{l}+\beta_{r}\right) \Gamma\left(\frac{1}{\nu}\right)} \exp \left(-\left(\frac{-x}{\beta_{l}}\right)^{\nu}\right) & x<0 \\ \frac{\nu}{\left(\beta_{l}+\beta_{r}\right) \Gamma\left(\frac{1}{\nu}\right)} \exp \left(-\left(\frac{x}{\beta_{r}}\right)^{\nu}\right) & x \geq 0\end{cases}
\begin{aligned} &\beta_{l}=\sigma_{l} \sqrt{\frac{\Gamma\left(\frac{1}{\nu}\right)}{\Gamma\left(\frac{3}{\nu}\right)}} \\ &\beta_{r}=\sigma_{r} \sqrt{\frac{\Gamma\left(\frac{1}{\nu}\right)}{\Gamma\left(\frac{3}{\nu}\right)}} \end{aligned}
ここで、\nu, \sigma_l, \sigma_rは以下のような意味を持つ。
- 分布の尖度を表すshapeパラメータ\nu
- 左右それぞれの裾の広さを表すscaleパラメータ\sigma_l^2, \sigma_r^2
また、\etaを1次のモーメント(つまり平均)とし、以下のように計算する。
\eta=\left(\beta_{r}-\beta_{l}\right) \frac{\Gamma\left(\frac{2}{v}\right)}{\Gamma\left(\frac{1}{v}\right)}
以上の4つのパラメータ\left(\eta, \nu, \sigma_{l}^{2}, \sigma_{r}^{2}\right)をH, B, D1, D2に関して求め、特徴量に加える。
実験
以上のようにして得られる特徴量を用いて、品質の推定や劣化の種類を分類できることが示されている。
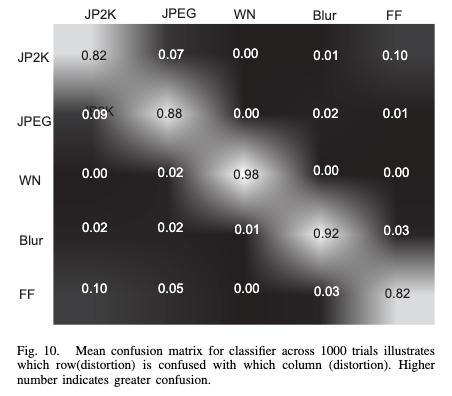
劣化の種類を推定する分類モデル
下図は、劣化の種類ごとのGGMのパラメータおよびAGGMのパラメータの散布図である。パッと見てわかるとおり、この時点で、さまざまな劣化の種類が比較的分離できていることがわかる。
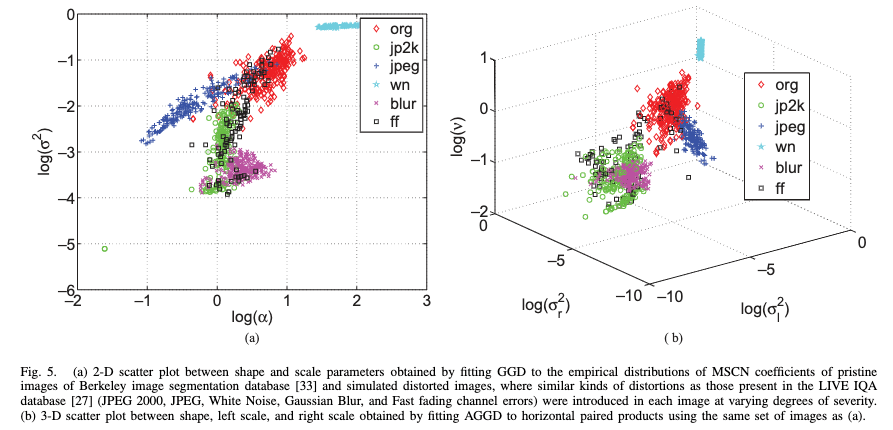
実際、この特徴量を用いてSVMを訓練し、劣化の種類をある程度分類できるモデルを構築できる。
品質を推定する回帰モデル
Live IQAデータベースでは、各画像について人間が評価したDMOS(differential mean opinion score)というスコアが付与されている。
このDMOSを直接推定するような回帰モデルをSVMによって構築し、BRISQUEのスコアとしている。
テストデータのDMOSと各種画像品質測定手法の出力とを比較し、スピアマンの順位相関係数(SROCC)および相関係数で、各手法を評価している。劣化の種類によって得意不得意はあるものの、全体(all列)としてはBRISQUEは比較的良い結果が得られている。
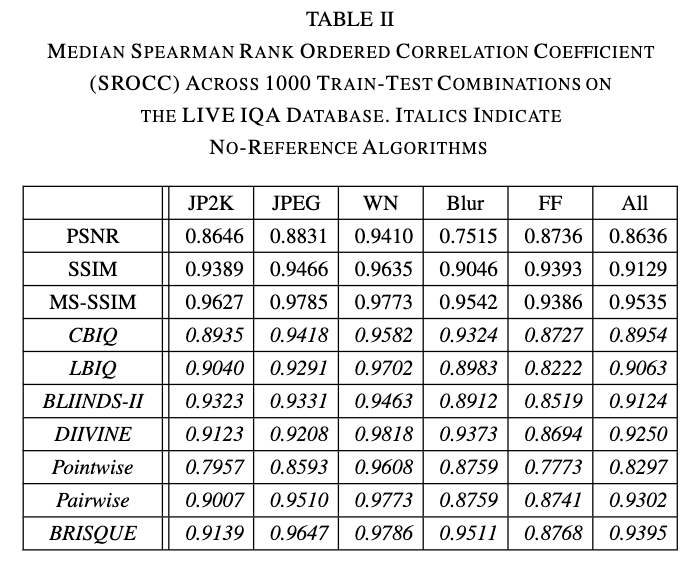
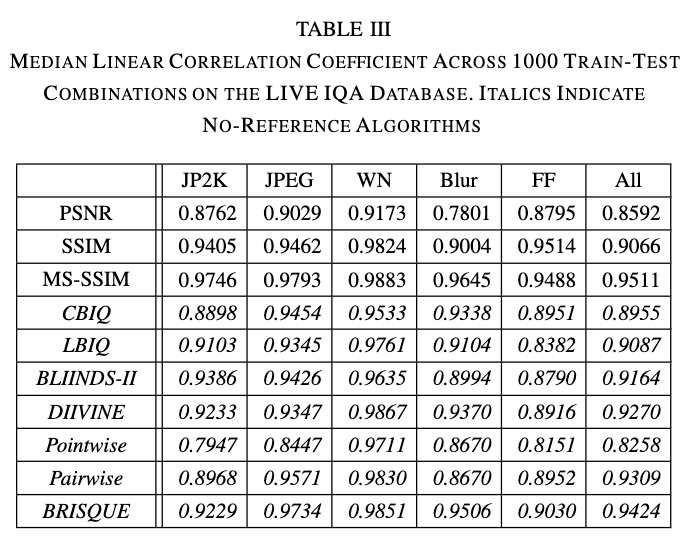
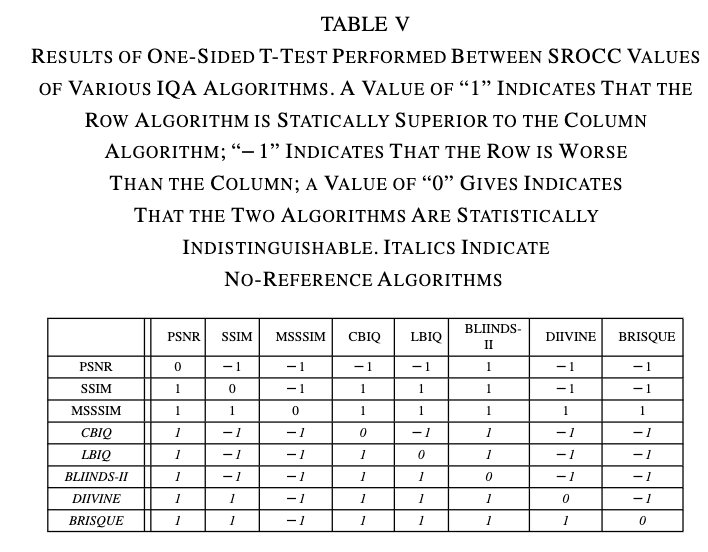
SROCCについては、t検定を用いて各種手法との比較をしたのが下の表である。Multi Scale SSIM(MSSSIM)以外の手法に対して、BRISQUEは有意に高い性能を得られている、ということが示されている。









Discussion