概要
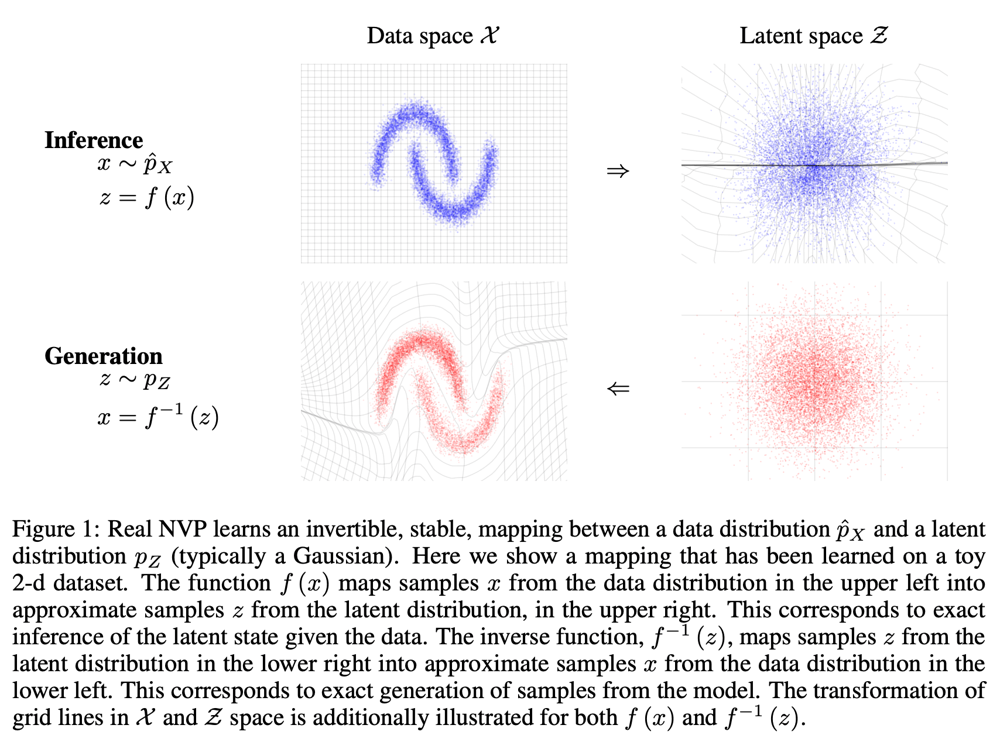
Real NVPは、データ分布\hat{p}_{X}と潜在変数分布p_{Z}(典型的にはガウス分布)の間を逆変換可能な全単射関数モデルを構築する手法。
書誌情報
- Dinh, Laurent, Jascha Sohl-Dickstein, and Samy Bengio. "Density estimation using real nvp." arXiv preprint arXiv:1605.08803 (2016).
- https://arxiv.org/abs/1605.08803
ポイント
全単射関数とヤコビアンの行列式
gがz \sim p_{Z}からx \sim p_{X}へのマッピングを行う関数であるとして、gが全単射であるとすれば、以下のような変数変換が成り立つ。
p_{X}(x)=p_{Z}(z)\left|\operatorname{det}\left(\frac{\partial g(z)}{\partial z^{T}}\right)\right|^{-1} = p_{Z}(f(x))\left|\operatorname{det}\left(\frac{\partial f(x)}{\partial x^{T}}\right)\right|
対数をとり、以下が成り立つ。通常、ヤコビアンの行列式は計算が大変だが、fの構造として特殊なネットワークを採用することで、簡単に計算ができるようになる。本研究ではそのためのCoupling Layerと呼ばれるネットワーク構造を提案している。
\log \left(p_{X}(x)\right)=\log \left(p_{Z}(f(x))\right)+\log \left(\left|\operatorname{det}\left(\frac{\partial f(x)}{\partial x^{T}}\right)\right|\right)
Coupling Layer
入力xの最初のdチャネルと残りのD- dチャネルを分割し、x_{1: d}, x_{d+1: D}を作る。分割された入力を用いて、同様に分割された出力を行う以下のような計算を考える。
\begin{gathered}
\begin{cases}
y_{1: d} & =x_{1: d} \\
y_{d+1: D} & =x_{d+1: D} \odot \exp \left(s\left(x_{1: d}\right)\right)+t\left(x_{1: d}\right)
\end{cases} \\
\Leftrightarrow
\begin{cases}
x_{1: d} &=y_{1: d} \\
x_{d+1: D}&=\left(y_{d+1: D}-t\left(y_{1: d}\right)\right) \odot \exp \left(-s\left(y_{1: d}\right)\right)
\end{cases}
\end{gathered}
上式の1つ目は順方向の計算で、2つ目は逆方向の計算である(入出力が入れ替わっている)。これは下図のような計算グラフで表せる。scale sとtransform tは共にR^{d} \mapsto R^{D-d}であり、順方向・逆方向で同じように使用され、複雑な逆関数の計算などを必要としない。にもかかわらず、全体としては逆関数が簡単に使えるという点が重要である。
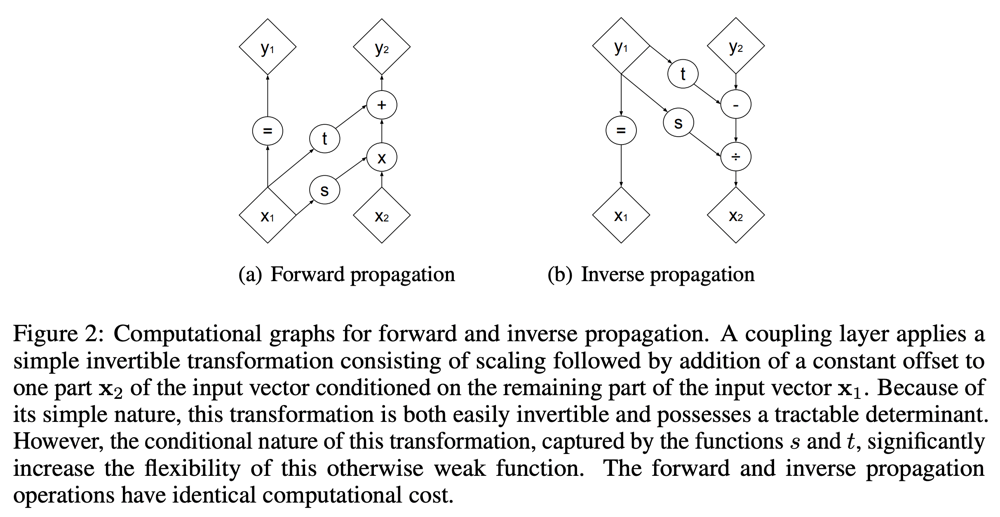
このような関数のヤコビアンは以下のようになる。
\frac{\partial y}{\partial x^{T}}=\left[\begin{array}{cc} \mathbb{I}_{d} & 0 \\ \frac{\partial y_{d+1: D}}{\partial x_{1: d}^{T}} & \operatorname{diag}\left(\exp \left[s\left(x_{1: d}\right)\right]\right) \end{array}\right]
このヤコビアンは下三角行列になっているため、行列式は対角成分の積\exp \left[\sum_{j} s\left(x_{1: d}\right)_{j}\right]であり、簡単に計算できる。
マスクによる実装
実装上は、以下のようなマスクbを使用し、{1:d}, {d+1:D}のチャネル分離を実現する。
y=b \odot x+(1-b) \odot(x \odot \exp (s(b \odot x))+t(b \odot x))
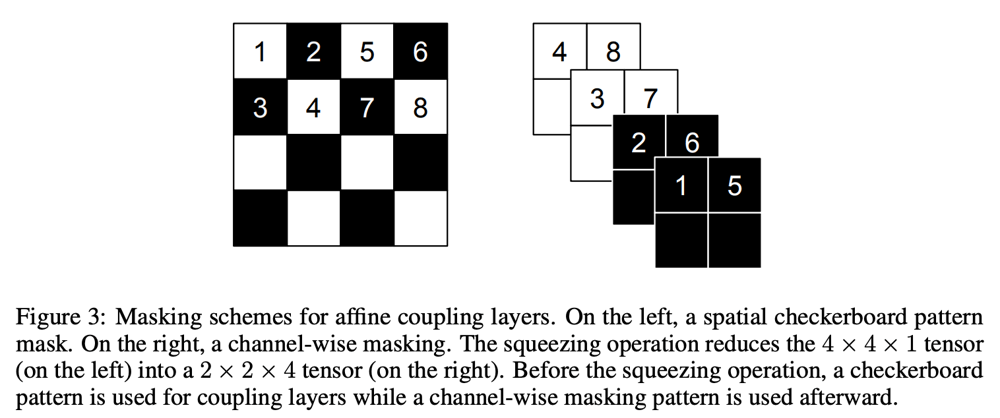
マスクbの0,1は、基本的にはチャネル方向の分割を表すが、画像特徴量においては画像の局所的な相関を利用し、下図左のようなチェッカーボードパターンでマスクを表現することもできる。その場合、下図左のような入力(H, W, C)を下図右のように(H/2, W/2, 4C)の形に並べ替え、Coupling Layerで演算したのち左の配置に戻す、ということを行える。なお、画像や特徴マップを対象とする場合は、s, tはConv層+活性化関数となる。
交互のマスク適用
マスクの形状が同一のまま、Coupling Layerを複数層重ねて適用すると、最初のdチャネルは入力の値のまま不変になってしまう。これは特徴抽出の効率上よくないので、下図のようにマスクを交互に反転させたCoupling Layerを適用する。
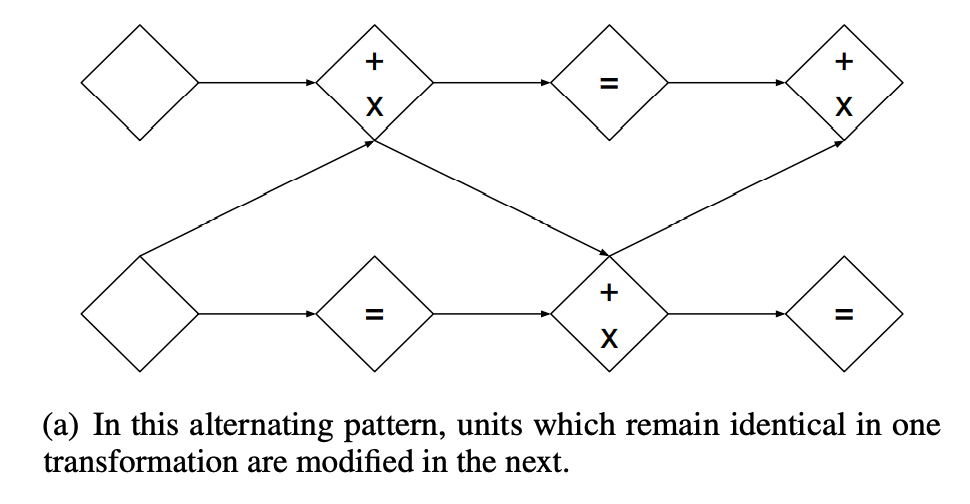
この合成関数のヤコビアンの行列式も、それぞれの関数のヤコビアンの行列式の積となり、簡単に求められる。
\begin{aligned} \frac{\partial\left(f_{b} \circ f_{a}\right)}{\partial x_{a}^{T}}\left(x_{a}\right) &=\frac{\partial f_{a}}{\partial x_{a}^{T}}\left(x_{a}\right) \cdot \frac{\partial f_{b}}{\partial x_{b}^{T}}\left(x_{b}=f_{a}\left(x_{a}\right)\right) \\ \operatorname{det}(A \cdot B) &=\operatorname{det}(A) \operatorname{det}(B) . \end{aligned}
マルチスケールアーキテクチャ
画像や特徴マップを入力とする時に、CNNでは、Poolingのような処理を挟み、サイズを縮小しつつ処理するのが一般的である。Real NVPでは、関数の可逆性を確保するために、2\times2\times Cの領域を1\times1\times 4Cへ変換するSqueezing操作を採用する。
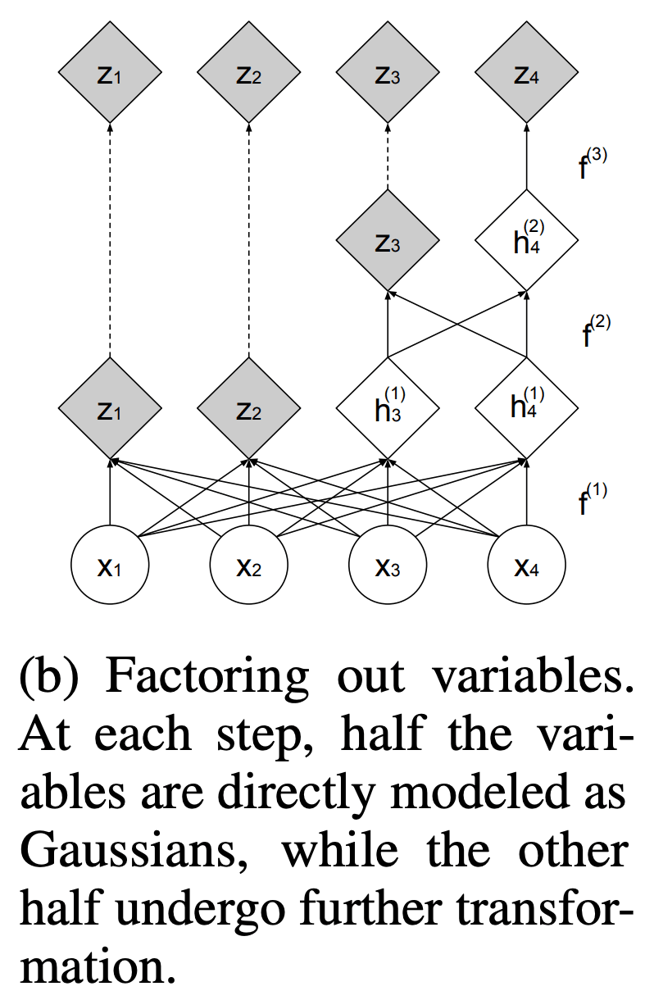
しかし、この操作は何度も適用するとその度にチャネルの次元数が大きくなっていくため、どこかでチャネル数を削減したほうが良い。そこで、一定の間隔で、出力の半分のチャネルを切り捨ててそのまま最終出力にもっていき、残りの半分を後続の層への入力に使用するfactoring outという方法を採用している。下式のように、最終的な出力は、途中切り捨てた出力z^iを結合し、z=\left(z^{(1)}, \ldots, z^{(L)}\right)となる。途中で切り出された出力も含め、ガウス事前分布が適用されることになる。
\begin{aligned} h^{(0)} &=x \\ \left(z^{(i+1)}, h^{(i+1)}\right) &=f^{(i+1)}\left(h^{(i)}\right) \\ z^{(L)} &=f^{(L)}\left(h^{(L-1)}\right) \\ z &=\left(z^{(1)}, \ldots, z^{(L)}\right) \end{aligned}
BatchNormalizationの利用
Batch Normalizationのような入力された特徴マップの統計量を利用するモジュールを可逆にするのは非常に難しいが、統計量としてrunning averageで代替することで可能になる。例えば、Batch Normalizationにおける平均\muと分散\sigma^2を処理中のバッチ内で計算するのではなく、running average\tilde{\mu}, \tilde{\sigma}^{2}に置き換えることで、可逆なモジュールとして利用できる。
x \mapsto \frac{x-\tilde{\mu}}{\sqrt{\tilde{\sigma}^{2}+\epsilon}}
ヤコビアンの行列式は以下のようになる。
\left(\prod_{i}\left(\tilde{\sigma}_{i}^{2}+\epsilon\right)\right)^{-\frac{1}{2}}






Discussion