🐶

【論文5分まとめ】Multiresolution Hash Encoding

2022/02/26に公開

概要

低コストなNeural Graphics PrimitiveであるMultiresolution Hash Encodingを提案。階層的なハッシュテーブル構造により、効率的な位置エンコーディングを実現。CUDAレベルでの最適化も組み合わせて行うことで、わずか数十秒でNeRFモデルを訓練できるなど、さまざまなアプリケーションでの訓練を高速化できる。

書誌情報

Müller, Thomas, et al. "Instant Neural Graphics Primitives with a Multiresolution Hash Encoding." arXiv preprint arXiv:2201.05989 (2022).
https://arxiv.org/abs/2201.05989
https://github.com/NVlabs/instant-ngp

ポイント

Neural Graphics Primitive

Neural GraphicsにおけるPrimitiveとは、位置情報から得られるコードであり、例えば、スカラー位置 $x \in \mathbb{R}$ に対して、以下のようなcosine表現があり得る。

\begin{aligned} \operatorname{enc}(x)=&\left(\sin \left(2^{0} x\right), \sin \left(2^{1} x\right), \ldots, \sin \left(2^{L-1} x\right)\right.\\ &\left.\cos \left(2^{0} x\right), \cos \left(2^{1} x\right), \ldots, \cos \left(2^{L-1} x\right)\right) \end{aligned}

Multiresolution Hash Encoding

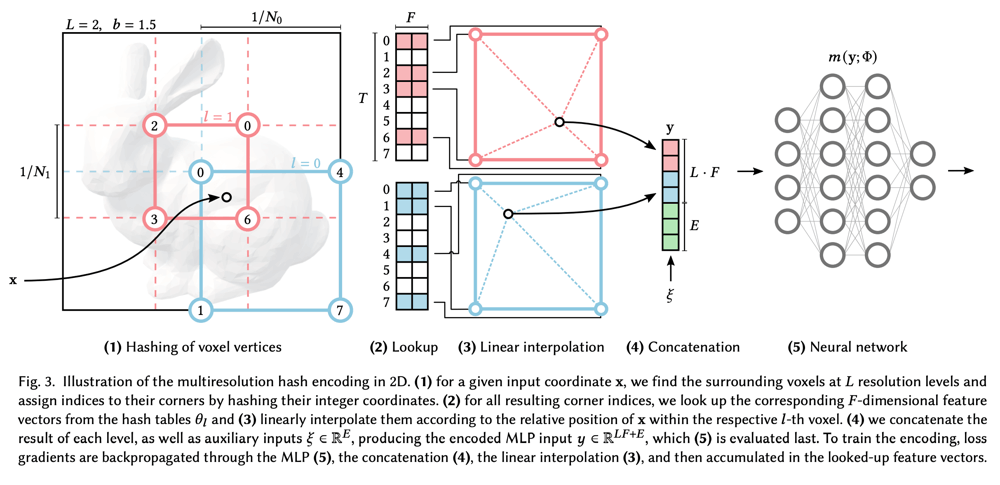
入力座標 $\mathbf{x} \in \mathbb{R}^d$ とする。下の図では、 $d=2$ の時を表している。

各階層の格子の数（解像度）は以下のように定義する。上図の例では、 $N_\text{min}=2, N_\text{max}=3$ であり、 $L=2, b=1.5$ となる。

N_{l}:=\left\lfloor N_{\min } \cdot b^{l}\right\rfloor

b:=\exp \left(\frac{\ln N_{\max }-\ln N_{\min }}{L-1}\right)

各階層では、 $\mathbf{x}$ の近傍にある格子点を参照する。上図の $l=0$ における近傍は青の四角の頂点であり、 $l=1$ における近傍は赤い四角の頂点である。

各格子点には、疑似乱数的なハッシュキーが下式によって与えられる。

h(\mathbf{x})=\left(\bigoplus_{i=1}^{d} x_{i} \pi_{i}\right) \quad \bmod T

$\pi_i$ は $i=1$ の時を除き、十分に大きな素数が使用され、具体的には、 $\pi_1=1, \pi_2=2654435761, \pi_3=805459861$ を用いている。 $\bigoplus$ は、bit-wise XORである。また、 $T$ はハッシュテーブルの大きさで、上図の例では $T=8$ であり、全階層で同じ大きさを採用する。

近傍の格子点のハッシュキーからハッシュテーブルを参照し、ハッシュ値（上図では $F=2$ 次元）を得て、 $\mathbf{x}$ の位置に応じた補間を行う。各階層で $F$ 次元のベクトルが得られるので、全体としては $L$ 階層の場合は $LF$ 次元のベクトルが得られることになる。

モデルによっては、位置情報のエンコード以外の入力が存在する。例えば、NeRFでは、視線の方向や材質を表す反射特性などが挙げられる。このような $E$ 次元の入力も組み合わせ、最終的な $LF+E$ 次元の入力が得られる。

上図は極めて単純な例ではあるが、実際には下の表のような値が使用されている。

以上のような仕組みによって得られる入力 $\mathbf{y} = \operatorname{enc}(\mathbf{x} ; \theta)$ を用いて、各種タスクのMLP $m(\mathbf{y} ; \Phi)$ への入力とする。

いくつかの論点

パフォーマンスとクオリティ

$T$ によって、メモリ消費量・クオリティとパフォーマンスのトレードオフをコントロールできる。また、 $F$ や $L$ も同様のトレードオフがあり、 $(F=2, L=16)$ が本研究では安定して各種モデルに適用できるパラメータであるとしている。

ハッシュの衝突

ハッシュテーブルは全階層で同じ大きさ $T$ であるため、本手法のハッシュテーブルに関する学習対象パラメータの大きさは、必ず $T \cdot L \cdot F$ になる。これはコンパクトなパラメータを可能にする。

低解像度の階層ではハッシュ衝突が起きず、単射的にハッシュ値が決まる一方で、高解像度の階層では $T$ の値によってハッシュ衝突の頻度が多くなってくる。例えば、最初の図で示した階層 $l=1$ では頂点の数は $9>T=8$ であるため、ハッシュキーの衝突が必ず生じることになる。

幸い、ハッシュキーは空間上にランダムに散らばっているため、全階層の同一点で同時に生じることはまず無い。また、各種タスクの再構成において重要な点（NeRFで言えば密度が高い点）と重要でない点（NeRFで言えば密度が低い点）があり、ハッシュ衝突を起こしている全ての点がいずれも重要な点であるということはほとんどない。

仮に、同程度に重要な点同士がある階層でハッシュ衝突を起こしていたとしても、その階層のハッシュテーブルは片方の点を重視して訓練が進み、近隣の別の階層のハッシュテーブルでもう片方の点を重視した訓練が進むだけであり、全体としてはとしてはいずれの重要な点に関しても訓練が進むことになる。

オンライン適応

本手法は、訓練中に $\mathbf{x}$ の分布が変化しても柔軟に訓練を進めることができる。例えば、訓練中のある時点で $\mathbf{x}$ がある特定の領域に集中してしまった場合でも、高解像度の階層におけるハッシュ衝突が少なくなり、むしろテーブルが正確に訓練されるだけで、何の不利益も生じない。

このような特性は、継続的に新しいデータが与えられるneural radiance cachingのようなモデルで有効に働く。

d-linear補間

補間なしでは、格子状の不連続な領域が生じてしまうので、格子点からの距離に応じた補間を行う必要がある。その場合の補間の重み（ $d-\text{linear}$ ）は、 $\mathbf{w}_{l}:=\mathbf{x}_{l}-\left\lfloor\mathbf{x}_{l}\right\rfloor$ とする。

このような標準的な線形補間以上に滑らかな補間（2次補間、3次補間）が必要な場合がある（例：法線ベクトルも再構成したい時）。その場合は、低コストの代替手段として、 $d-\text{linear}$ の重みに対して、以下のようなSmooth step関数を適用することで、高次の補間を代替することを提案している（より高次の補間については別途Smooth step関数 $S_n$ を設計する必要がある）。

S_{1}(x)=x^{2}(3-2 x)

S_{1}^{\prime}(x)=6 x(1-x)

実装

実装状の工夫を箇条書きでまとめておく。

実装は、tiny-cuda-nn frameworkを使用している。
ハッシュテーブルをGPUのL2キャッシュ（RTX 3090で6MB）に格納することで、高速な演算を可能にしている。そのため、 $T$ のサイズがキャッシュに収まる範囲内であれば、訓練時間はほとんど変化しない。
OptimizerはAdamを使用し、 $\beta_1=0.9, \beta_2=0.99, \epsilon=10^{-15}$ を採用している。 $\beta_1, \beta_2$ はそれほど敏感ではなかったが、 $\epsilon$ を十分に小さくすることで高速な収束が確認されたという。これは、ハッシュテーブルにかかる勾配がスパースで小さいことと関係がある。
長期の訓練による発散を抑制するため、ある程度訓練が進んでから、MLPに対してのみ弱いL2正則化（重みは $10^{-6}$ ）を適用する。ハッシュテーブルに対してはL2正則化は適用しない。
$T$ がバッチサイズよりも十分に大きい時、ハッシュテーブルに対する勾配が0になることがある。その場合はAdamのステップをスキップすることで、10%以内のパフォーマンス改善が見られる。