概要
Self-Attentionを置き換えるFocal-Modulationを提案。これを利用したFocalNetにより、各種タスクでSwin-TransformerやConvNeXtを凌駕する性能を達成。
書誌情報
ポイント
Window-wise Self-Attentionの復習
Self-Attentionの処理の流れを図示すると下図のように表される。
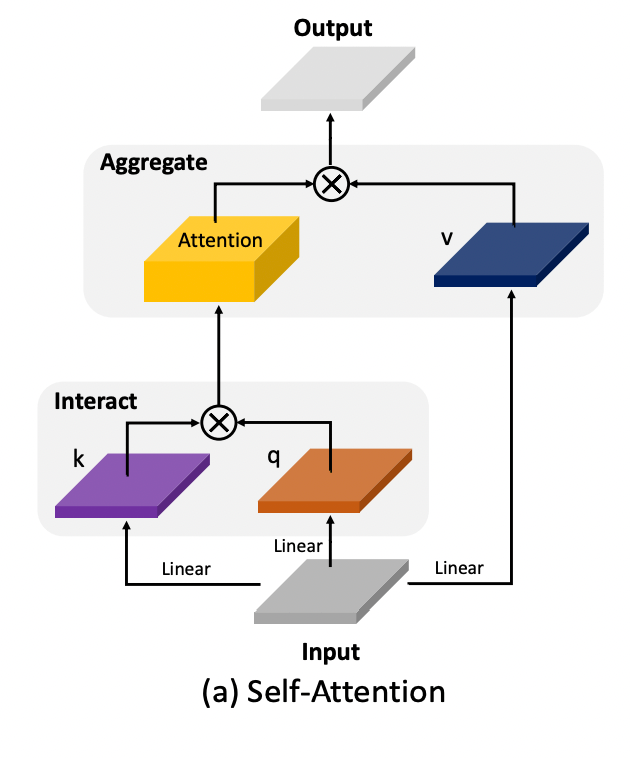
通常のSelf-Attentionでは、Q, Kの相互作用を計算する時に、トークン長の2次の計算量が発生する。これを抑制するために、Swin-Transformerなどでは、Window-wiseなSelf-Attentionが使用される。
数式的には、以下のように表される。
\boldsymbol{y}_{i}=\sum_{j \in \mathcal{N}(i)} \operatorname{Softmax}\left(\frac{q\left(\boldsymbol{x}_{i}\right) k(\mathbf{X})^{\top}}{\sqrt{C}}\right)_{j} v\left(\boldsymbol{x}_{j}\right)
ここで、q, k, vは線形変換である。X \in \mathbb{R}^{H \times W \times C}であり、\mathcal{N(i)} はWindowによって限定されるiの近隣インデックス集合である。Windowのサイズwを用いると、この計算の複雑さは、\mathcal{O}(HW\times(3C^2+2Cw^2))となる。何の工夫も行っていない標準的なSelf-Attentionでは、w=HWであるため、計算量が非常に大きくなるところを、Windowの導入によって抑えている。
抽象化すれば、Self-Attentionのような操作は以下のように書くことができる。\mathcal{T}はあるトークンと周囲のトークンとの相互作用による重みの計算を表し、\mathcal{M}は重みを用いた周辺の情報の集約操作と言える。
\boldsymbol{y}_{i}=\mathcal{M}_{1}\left(\mathcal{T}_{1}\left(\boldsymbol{x}_{i}, \mathbf{X}\right), \mathbf{X}\right)
Focal-Modulation
提案手法であるFocal-Modulationでは、この操作の順番を入れ替える。すなわち、まず先に\mathcal{M}を用いた周辺情報の集約操作を行い、\mathcal{T}を用いて周辺情報とトークンとの相互作用を働かせる、という順番である。
\boldsymbol{y}_{i}=\mathcal{T}_{2}\left(\mathcal{M}_{2}\left(\boldsymbol{x}_{i}, \mathbf{X}\right), \boldsymbol{x}_{i}\right)
具体的には、以下のような計算を行う。\mathcal{T}はもはや線形変換(q,h)と単純な要素積として表される。他方、\mathcal{M}はやや複雑な機構になっている。
\boldsymbol{y}_{i}=q\left(\boldsymbol{x}_{i}\right) \odot h\left(\sum_{\ell=1}^{L+1} \boldsymbol{g}_{i}^{\ell} \cdot \boldsymbol{z}_{i}^{\ell}\right)
Focal-Modulationの構造
Focal-Modulationは以下のような構造になっている。(c)のContext Aggregationが、上式の\mathcal{M}に対応する。
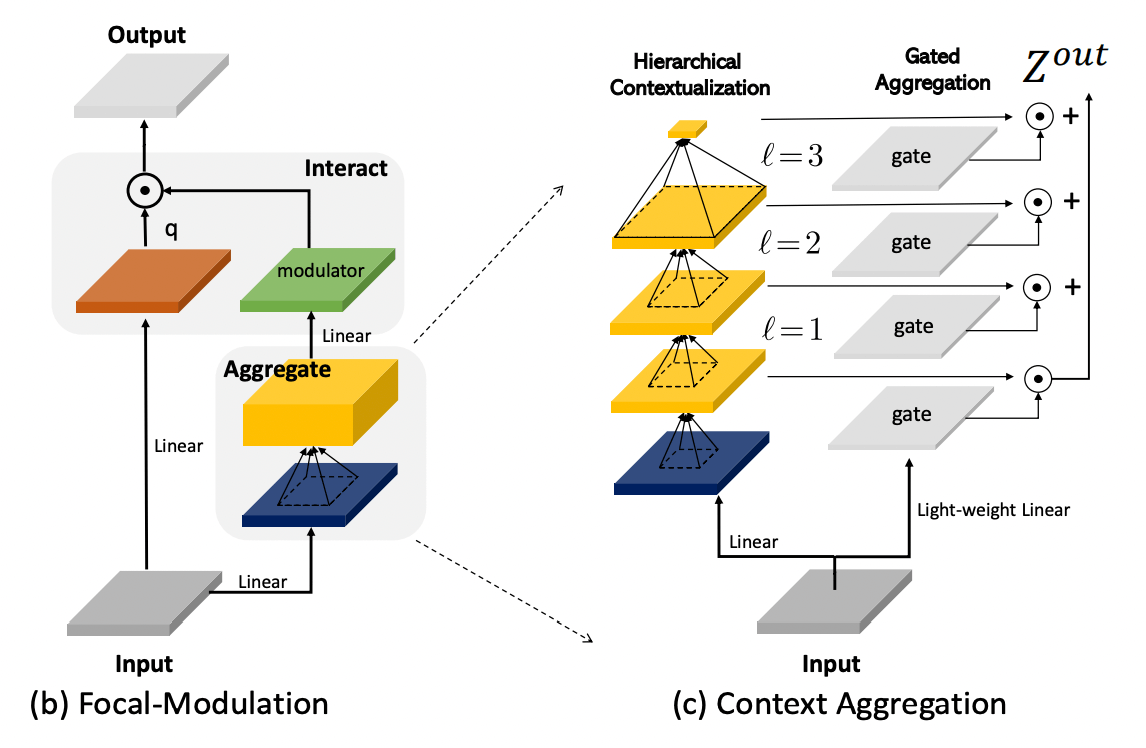
Context Aggregationは、徐々に大きくなるカーネルサイズのDepth-wise Conv層を重ねたHierachcal Contextualizationと、空間的な重みづけを行うGate Aggregationからなる。以下、それぞれについて詳しく見ていく。
Hierachcal Contextualization
まず、入力を新しい空間へと投影する線形変換f_zを適用する。これによって、上図(c)の青い特徴マップが得られる。
\mathbf{Z}^{0}=f_{z}(\mathbf{X}) \in \mathbb{R}^{H \times W \times C}
次に、L個の2次元 Conv層f_{a}^{\ell}を適用する。ここで、Conv層はDepth-wiseであり、そのカーネルサイズk^{\ell}は3, 5, 7と2ずつ大きくなる。実際のFocalNetにおいては、Lは2または3が採用され、そこまで極端な階層数ではない。
\mathbf{Z}^{\ell}=f_{a}^{\ell}\left(\mathbf{Z}^{\ell-1}\right) \triangleq \operatorname{GeLU}\left(\operatorname{Conv}_{d w}\left(\mathbf{Z}^{\ell-1}\right)\right)
このような多段階のConv層によって得られる特徴マップは、局所的な特徴から大域的な特徴へと徐々に担当する範囲が変わることが期待されている。各段階での実質的な受容野のサイズr^{\ell}は、r^{\ell}=1+\sum_{i=1}^{\ell}\left(k^{\ell}-1\right)と書ける。例えば、\ell=3の時の受容野のサイズはr^{\ell=3} = 1 + (3-1) + (5-1) + (7-1)=13となる。
さらに、最後の出力\mathbf{Z}^{L}に対してGlobal Average Poolingを適用し、大域的な特徴量\mathbf{Z}^{L+1}を得る。
\mathbf{Z}^{L+1}=\text { Avg-Pool }\left(\mathbf{Z}^{L}\right)
Gated Aggregation
このようにして得られた\mathbf{Z}^{1}, \mathbf{Z}^{2}, ..., \mathbf{Z}^{L+1}に対して、空間的な重みづけを行い、足し合わせることで最終的な出力\mathbf{Z}^{\text{out}}を得る。このようなGate機構の目的は、各クエリに対し、異なる階層ごとの重みづけを行うことにある。
\mathbf{Z}^{o u t}=\sum_{\ell=1}^{L+1} \mathbf{G}^{\ell} \odot \mathbf{Z}^{\ell}
Gate\mathbf{G}のサイズは\mathbb{R}^{H \times W \times (L+1)}であり、入力\mathbf{X}に対する線形変換f_{g}によって得られる。
\mathbf{G}=f_{g}(\mathbf{X}) \in \mathbb{R}^{H \times W \times(L+1)}
FocalNet
以下に、Focal-Modulationを用いたネットワーク構造FocalNetのパラメータを示す。SRFとLRFの違いは受容野の大きさの違いを表すが、実態としてはL=2かL=3かの違いのみである。LRFの方が一貫して精度は向上するが、やや速度は劣化する。
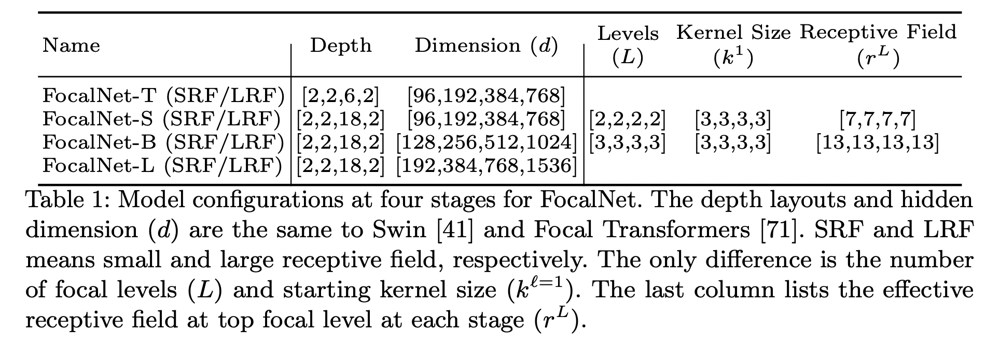
Focal-Modulationの効果
Focal0Modulationの利点
まず、Focal-Modulationの利点をまとめると、以下のようになる。
- 普通の2次元Conv層で実装できる
- Swin-TransformerのようなWindowによる分割操作を必要としない
- 2, 3個スタックするだけで、大きい受容野を実現できる
ModularとGateの可視化
FocalNetの最終レイヤーのModular(h\left(\sum_{\ell=1}^{L+1} \boldsymbol{g}_{i}^{\ell} \cdot \boldsymbol{z}_{i}^{\ell}\right))の全チャネルを平均して可視化すると、下図のように、前景領域を強調するようなマップが得られる。

また、Gateの方を可視化してみると、各レベルで比較的異なる領域に注意が向いているということが確認できる。このことから、各レベルで異なる特徴を強調する役割を担っていると考えられる。
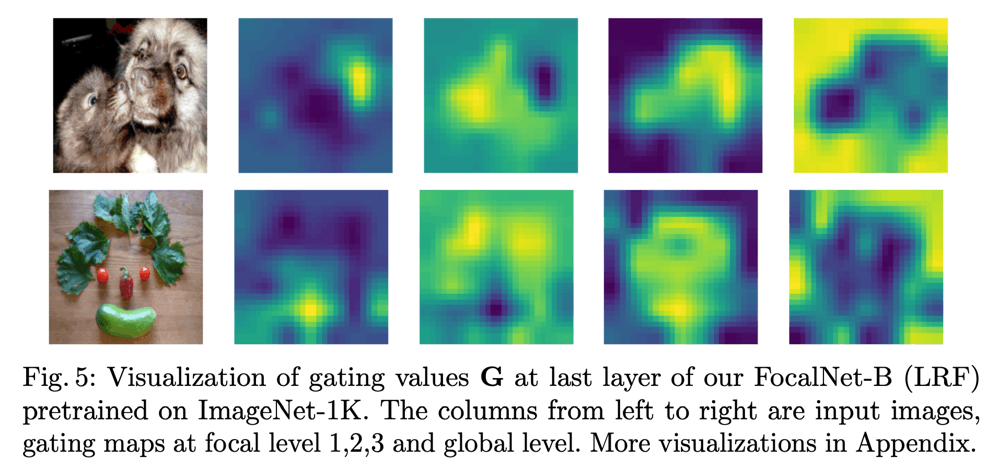
計算量
計算量としては、\mathcal{O} ( H W \times (3C^{2}+C(2 L+3)+C \sum_{\ell}(k^{\ell})^{2} ) )となり、L, (k^\ell)^2はCよりも十分小さいので、Windown-wise Self-Attentionと同程度のオーダーとなることがわかる。
実験
詳細は省略する。
- 画像分類においては、同程度のパラメータ数・受容野のSwin-Transformer, Focal-Transformerを速度・精度の両面で上回っていることを確認している。また、ViTにおけるSelf-Attentionを置換したバージョンでも、通常のViTを凌駕する性能を得ている。
- 物体検出、セグメンテーションタスクにおいても現在のSoTAをおおむね凌駕する性能を達成している。






Discussion