概要
Normalization Flowベースのリアルタイムで実行可能な軽量な異常検出手法CLFOW-ADを提案。
書誌情報
ポイント
理論的背景
特徴抽出とガウス事前分布
分類タスクに使用するようなCNN h(\boldsymbol{\lambda})を考える。このCNNを訓練するということは、以下のKL Divergenceと正則化項からなる損失関数を最小化するようなパラメータ\boldsymbol{\lambda}を求めることである。
\underset{\boldsymbol{\lambda}}{\arg \min } D_{K L}\left[Q_{\boldsymbol{x}, \boldsymbol{y}} \| P_{\boldsymbol{x}, \boldsymbol{y}}(\boldsymbol{\lambda})\right]+\alpha R(\boldsymbol{\lambda})
-
P_{\boldsymbol{x}, \boldsymbol{y}}(\boldsymbol{\lambda})はモデルの分布
-
Q_{\boldsymbol{x}, \boldsymbol{y}}は教師データの分布
- L2正則化を\boldsymbol{\lambda}だけでなく、CNNによって抽出された特徴量\boldsymbol{z}に対しても適用することがある。これは、\boldsymbol{z}の事前分布として多次元ガウス分布が適用されていることと等価である。
マハラノビス距離による異常検出
データが正規分布に従っていると仮定する時によく利用される異常の度合いの指標として、マハラノビス距離がある。特徴量\boldsymbol{z}が\mathcal{N}(\mu, \boldsymbol{\Sigma})に従っているとする。その時の確率密度関数は以下のように書くことができる。
p_{Z}(\boldsymbol{z})=(2 \pi)^{-D / 2} \operatorname{det} \boldsymbol{\Sigma}^{-1 / 2} e^{-\frac{1}{2}(\boldsymbol{z}-\boldsymbol{\mu})^{T} \boldsymbol{\Sigma}^{-1}(\boldsymbol{z}-\boldsymbol{\mu})}
これに対するマハラノビス距離は以下のように定義される。
M(\boldsymbol{z})=\sqrt{(\boldsymbol{z}-\boldsymbol{\mu})^{T} \boldsymbol{\Sigma}^{-1}(\boldsymbol{z}-\boldsymbol{\mu})}
真のパラメータ\boldsymbol{\mu}, \boldsymbol{\Sigma}は不明なので、実際には\mathcal{D}_{\text {train }}から推定された値\hat{\boldsymbol{\mu}}, \hat{\boldsymbol{\Sigma}}を用いる。
異常データからサンプルされた\boldsymbol{z}はM(\boldsymbol{z})が大きくなり、これを利用して適当な閾値を決めることで、異常検知を行える。
Flowフレームワーク
Normalization Flowでは、任意の密度関数p_{Z}(\boldsymbol{z})と多次元標準正規分布p_{U}(\boldsymbol{u})とを対応づける可逆な関数g^{-1}: Z \rightarrow Uを得ることを目標とする。f, gについて、以下の関係が成り立ち、共通のパラメータ\boldsymbol{\theta}を使用する。
\boldsymbol{z}=g(\boldsymbol{u}, \boldsymbol{\theta}), \boldsymbol{u}=g^{-1}(\boldsymbol{z}, \boldsymbol{\theta})
ここから、対数尤度\log \hat{p}_{Z}(\boldsymbol{z}, \boldsymbol{\theta})が以下のように得られる。
\log \hat{p}_{Z}(\boldsymbol{z}, \boldsymbol{\theta})=\log p_{U}(\boldsymbol{u})+\log |\operatorname{det} \boldsymbol{J}|
\boldsymbol{u} \sim \mathcal{N}(\mathbf{0}, \boldsymbol{I}), \boldsymbol{J}=\nabla_{\boldsymbol{z}} g^{-1}(\boldsymbol{z}, \boldsymbol{\theta})であり、ヤコビアン\boldsymbol{J}の計算は本来はそれなりに複雑だが、Real NVPのようにCoupling Layerで構成されている場合は簡単に求めることができる。
ここで、真の分布p_{Z}(\boldsymbol{z})に\hat{p}_{Z}(\boldsymbol{z}, \boldsymbol{\theta})に近づけられるような\boldsymbol{{\theta}}は、以下のようなReversed KL Divergenceを最小化することで得られる。
D_{K L}\left[\hat{p}_{Z}(\boldsymbol{z}, \boldsymbol{\theta}) \| p_{Z}(\boldsymbol{z})\right]
これは、以下の損失関数をSGDによって最小化することで実現できる。
\mathcal{L}(\boldsymbol{\theta})=\mathbb{E}_{\hat{p}_{Z}(\boldsymbol{z}, \boldsymbol{\theta})}\left[\log \hat{p}_{Z}(\boldsymbol{z}, \boldsymbol{\theta})-\log p_{Z}(\boldsymbol{z})\right]
一例として、この損失関数は、p_{Z}(\boldsymbol{z})が多次元正規分布の場合はマハラノビス距離M(\boldsymbol{z})を用いて以下のように書ける。E^{2}(\boldsymbol{u})=\|\boldsymbol{u}\|_{2}^{2}はユークリッド距離の自乗である。
\mathcal{L}(\boldsymbol{\theta})=\mathbb{E}_{\hat{p}_{Z}(\boldsymbol{z}, \boldsymbol{\theta})}\left[\frac{M^{2}(\boldsymbol{z})-E^{2}(\boldsymbol{u})}{2}+\log \frac{|\operatorname{det} \boldsymbol{J}|}{\operatorname{det} \boldsymbol{\Sigma}^{-1 / 2}}\right]
Normalization Flowでは、多次元正規分布ではない任意の密度関数p_{Z}(\boldsymbol{z})を推定でき、特徴抽出にしようするEncoderの特性によらない、より自然な異常検出モデルを構築できると考えられる。
CFLOW
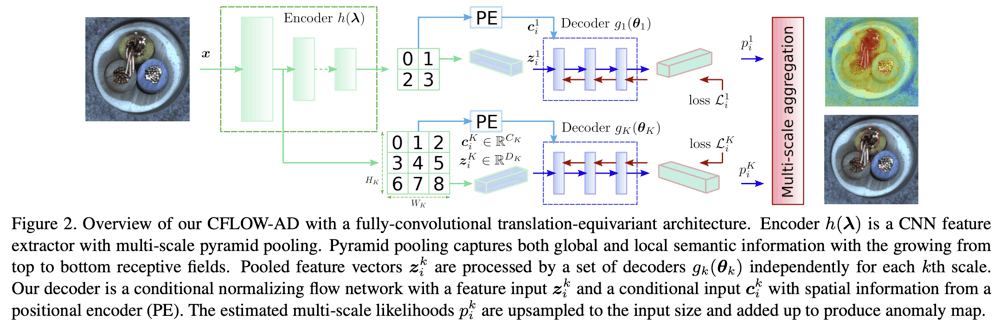
CFLOWの構造
本研究が提案するモデルであるCFLOWは、Encoderh(\boldsymbol{\lambda})とスケールに応じたK個の独立したDecoderg_k(\boldsymbol{\theta_k})からなる。
Encoderは、複数のスケールからなる特徴ピラミッドを出力する。画像中の異常は、さまざまな見た目、大きさ、形で現れるので、特徴抽出の多様性を確保する必要があるため、特徴ピラミッド構造を採用している。Encoderそのものの訓練はImageNetや各種自己教師あり学習によって訓練される。
Decoderは、Encoderの各スケールでの出力\boldsymbol{z}を多次元標準正規分布に従う点\boldsymbol{u}へとマッピングできるようなモデルが求められる。Decoderは一連のCoupling Layerから構成されるが、効率的な表現のために、位置情報を用いた条件付きモデルを採用する。これは、下図のような構造を持ち、特徴マップ上の特定の位置をもとに得られるPositional Encodingを条件\boldsymbol{c}として使用する。
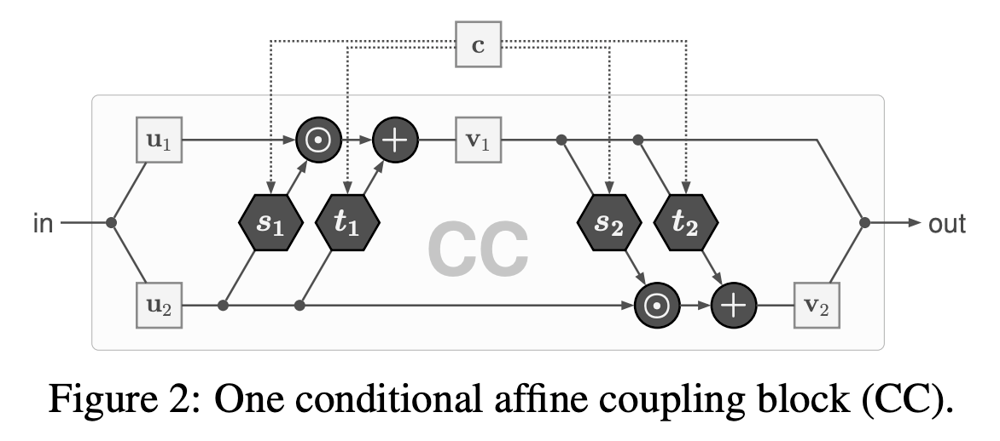
"Guided Image Generation with Conditional Invertible Neural Networks"より抜粋
特徴量の次元D_kとPositionalEncodingの次元C_kを組み合わせるので、Coupling Layerに含まれる全結合層のカーネルのサイズは\left(D_{k}+C_{k}\right) \times\left(D_{k}+C_{k}\right)となる。
損失関数
CFLOWのDecoderは、以下の損失関数を最小化することによって訓練される。Nは訓練データセットのサイズを表す。
\mathcal{L}(\boldsymbol{\theta}) =D_{K L}\left[p_{Z}(\boldsymbol{z}) \| \hat{p}*{Z}(\boldsymbol{z}, \boldsymbol{c}, \boldsymbol{\theta})\right] \approx \frac{1}{N} \sum_{i=1}^{N}\left[\frac{\left\|\boldsymbol{u}_{i}\right\|_{2}^{2}}{2}-\log \left|\operatorname{det} \boldsymbol{J}_{i}\right|\right]+\text { const }
\boldsymbol{u}_{i}=g^{-1}\left(\boldsymbol{z}_{i}, \boldsymbol{c}_{i}, \boldsymbol{\theta}\right)であり、\boldsymbol{J}_{i}=\nabla_{\boldsymbol{z}} g^{-1}\left(\boldsymbol{z}_{i}, \boldsymbol{c}_{i}, \boldsymbol{\theta}\right)である。前述の通り、\operatorname{det} \boldsymbol{J}_{i}は簡単に計算できる。
推論処理
訓練済みの各スケールのDecoderg_{k}\left(\hat{\boldsymbol{\theta}}_{k}\right)を用いて、テストデータに対して以下のように対数尤度を計算することができる。
\log \hat{p}_{Z}\left(\boldsymbol{z}_{i}, \boldsymbol{c}_{i}, \hat{\boldsymbol{\theta}}\right)=-\frac{\left\|\boldsymbol{u}_{i}\right\|_{2}^{2}+D \log (2 \pi)}{2}+\log \left|\operatorname{det} \boldsymbol{J}_{i}\right|
これを用いて、スケールkの位置iでの予測正常確率\hat{p}_i^kは以下のように書ける。
\hat{p}_i^k = e^{\log \hat{p}_{Z}\left(\boldsymbol{z}_{i}^{k}, \boldsymbol{c}_{i}^{k}, \hat{\boldsymbol{\theta}}_{k}\right)}
各スケールでの結果をbilinear補間し、入力画像のサイズまで拡大した\boldsymbol{P}_{k}をもとに、以下のように集約することで、異常度を表すマップを算出できる。
\boldsymbol{S}=\max \left({\sum_{k=1}^{K} \boldsymbol{P}_{k}}\right)-\sum_{k=1}^{K} \boldsymbol{P}_{k}
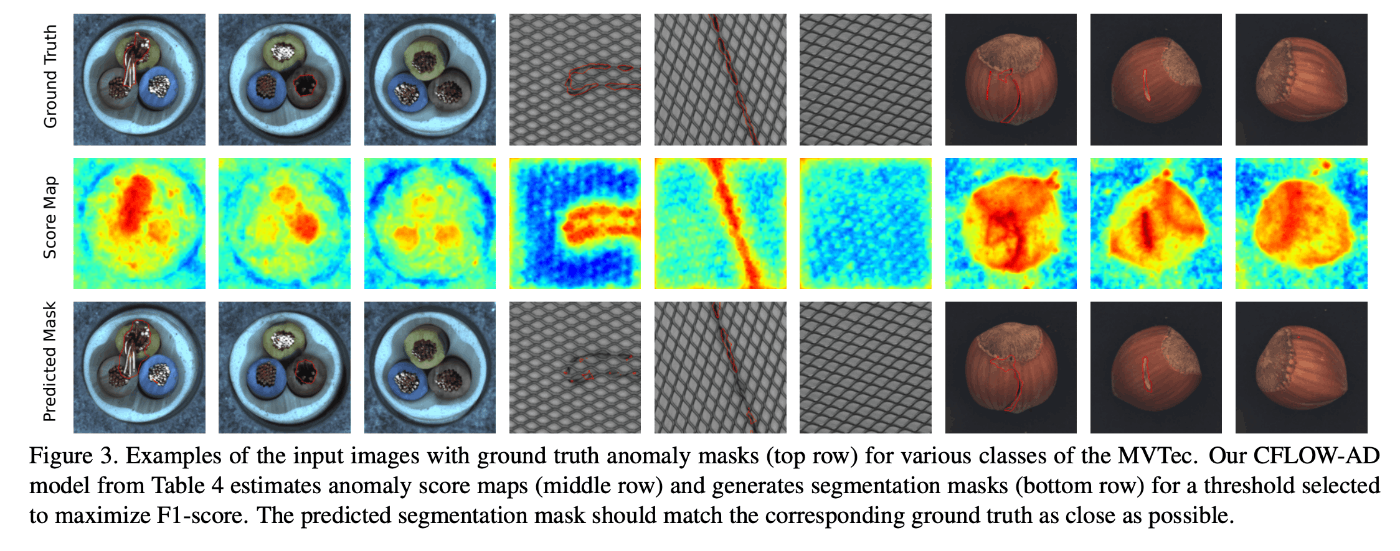
以下の図は、出力される異常度マップの例である。
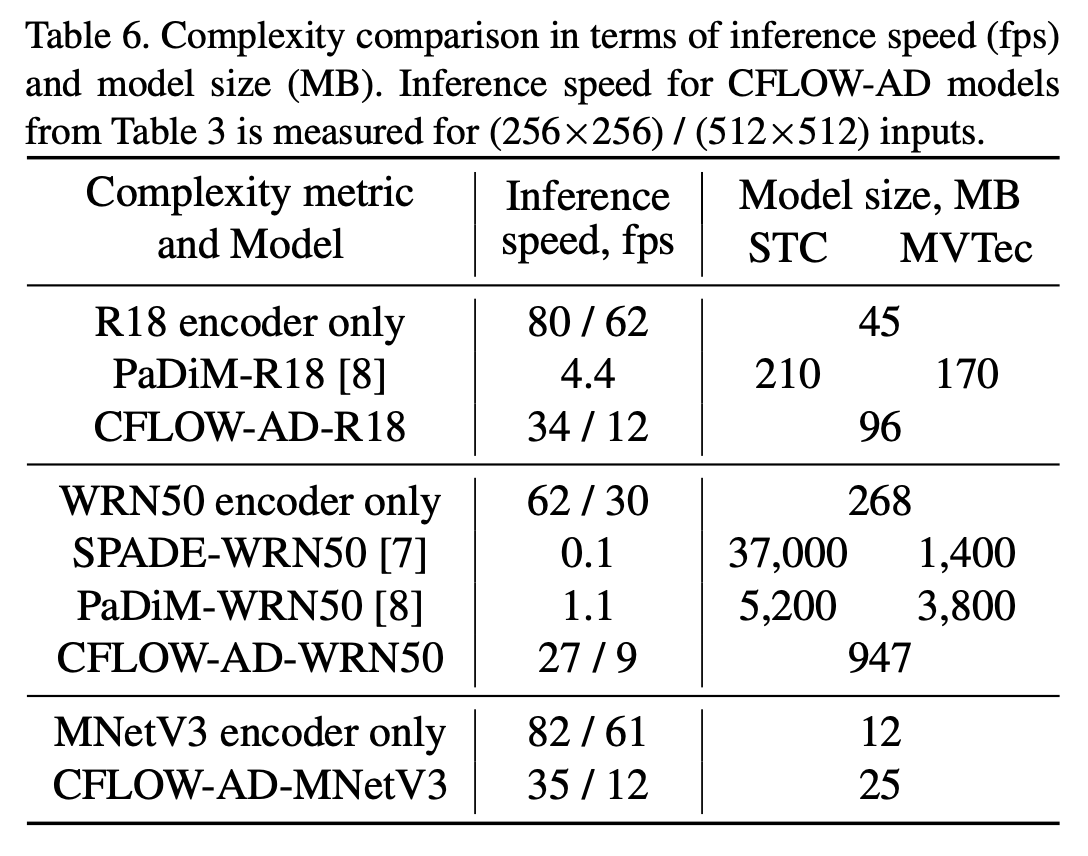
推論速度
CFLOWのDecoderは複数の全結合層からなるだけであり、以下の表に示すように、既存手法と比べて非常に高速に推論できる。
実験
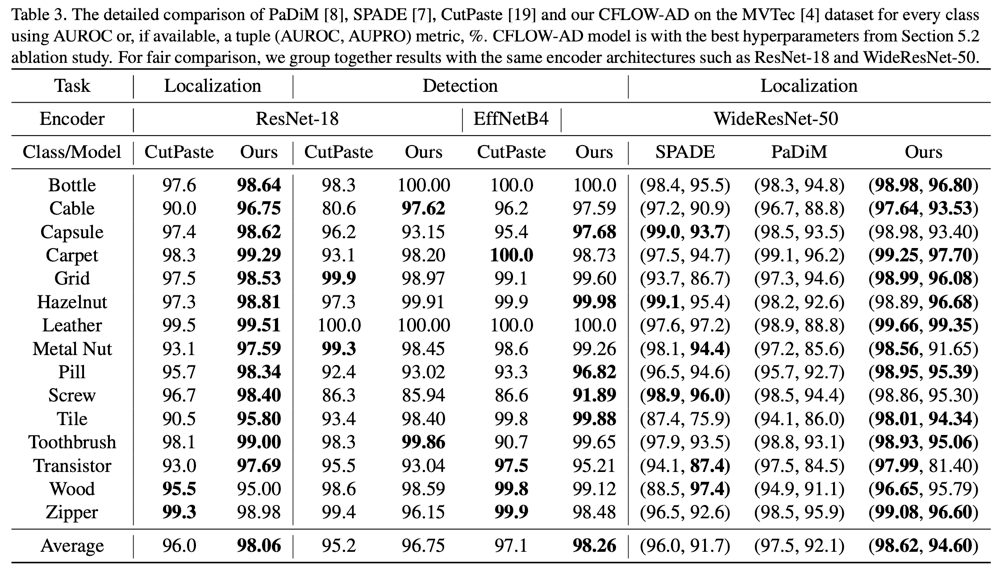
以下に示すのは、MVTecデータセットの各カテゴリーでの精度を、既存手法と比べたものである。既存手法と条件を揃えるために、使用するEncoderの構造を変えつつ、検出やLocalizationの精度を測定し、概ね既存手法を凌駕する精度を得ている。





Discussion