概要
物体検出の損失関数であるIoU損失およびGeneralized IoU(GIoU)損失の欠点を分析し、その欠点を克服することにより、早期の収束と性能向上を実現したDistance-IoU(DIoU)損失および Complete IoU(CIoU)損失を提案している。また、DIoU損失はNMSのスコアとしても適切であることを示している。
書誌情報
- Zheng, Zhaohui, et al. "Distance-IoU loss: Faster and better learning for bounding box regression." Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 34. No. 07. 2020.
- 公式実装
ポイント
IoU損失とGIoU損失の分析
IoU損失
IoUの定義は、予測矩形Bと 真の矩形領域B^{gt}を用いて以下のように与えられる。
I o U=\frac{\left|B \cap B^{g t}\right|}{\left|B \cup B^{g t}\right|}
IoUを用いて、IoU損失は、以下のように与えられる。
\mathcal{L}_{I o U}=1-IoU
予測が真の矩形に等しい時\mathcal{L}_{I o U}=0となり、予測が真の矩形と一切重なっていない場合は\mathcal{L}_{I o U}=1となる。
IoU損失の問題点は、予測と真の矩形の間に重なりがない場合、それらがすぐ近くにあるか遠くにあるかにかかわらず、IoU損失に変化が無いということにある。そのため、予測矩形を真の矩形に近づけるために必要な勾配が発生せず、適切に訓練が進まないという問題が生じてしまう。
GIoU損失
GIoU損失は、上記のIoU損失の欠点を克服した損失関数である。
IoU損失の問題を避けるために、GIoU損失では、2つの矩形を囲む最小の矩形Cを使用し、以下のように損失を定義する。
\mathcal{L}_{G I o U}=1-I o U+\frac{\left|C-B \cup B^{g t}\right|}{|C|}
GIoU損失では、予測と真の矩形の間に重なりが生じていない場合であっても、予測が真の矩形から遠く離れるほど損失が大きくなるため、適切に訓練が進む。
しかし、\left|C-B \cup B^{g t}\right|が0または小さい時、ほとんどIoU損失と変わらなくなってしまう。つまり、2つの矩形のいずれかが片方を含んでしまう場合、小さい方がどこに位置していても損失は変化しない。
GIoU損失を用いると、長い訓練によって収束はするが、まず最初に真の矩形と重なるように予測矩形を大きめに取る方向へ訓練が進み、その後矩形の大きさが調整されるように訓練が進むということが実験的に示されており、非効率であるといえる。
DIoU損失とCIoU損失
DIoU損失
GIoU損失の欠点を克服するために、DIoU損失では、予測と真の矩形の中心間の距離d=\rho\left(\mathbf{b}, \mathbf{b}^{g t}\right)をペナルティとして導入する。スケール不変性を持たせるために、2つの矩形を囲む矩形の対角線の長さcも用いた正規化された距離をペナルティにし、DIoU損失を以下のように定義している。
\mathcal{L}_{D I o U}=1-I o U+\frac{\rho^{2}\left(\mathbf{b}, \mathbf{b}^{g t}\right)}{c^{2}}
以下の図は、dとcの関係を図示したものである。

DIoU損失を用いると、\left|C-B \cup B^{g t}\right|=0の場合でも予測矩形の中心を真の矩形の中心へと近づける方向へと訓練が進む。以下の図はそのような場合のIoU損失, GIoU損失, DIoU損失を比較したものである。IoU損失とGIoU損失は予測矩形がどこにあっても同じ値だが、DIoU損失は予測矩形と真の矩形の中心位置が近いほど損失が小さくなることがわかる。そのため、DIoU損失はGIoU損失よりも素早い収束を実現できる。

CIoU損失
著者らは、2つの矩形の同一性は以下の3点によって得られるとしている。
- 矩形間の重なりが大きい
- 矩形(の中心)間の距離が近い
- 矩形のアスペクト比の近さ
DIoUは最初の2つは満たしているが、最後のアスペクト比に関しては無頓着である。よって、アスペクト比も損失に盛り込むことでより早い収束が見込まれる。この損失をCIoUとして提案している。
CIoU損失は以下のように定義される。vはアスペクト比の差異を表す指標で、\alphaはDIoUとのバランスを取るための係数である。
\mathcal{L}_{C I o U}=1-I o U+\frac{\rho^{2}\left(\mathbf{b}, \mathbf{b}^{g t}\right)}{c^{2}}+\alpha v
また、v, \alphaは以下のように定義される。
v=\frac{4}{\pi^{2}}\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right)^{2}
\alpha=\frac{v}{(1-I o U)+v}
なお、vの勾配は以下のように書ける。w,hは矩形回帰の場面では[0, 1]であり\frac{1}{w^2+h^2}は非常に大きな値になりがちなので、収束のための安定性のために、\frac{1}{w^2+h^2}は1に置換したほうが良いとのことである。
\begin{aligned} \frac{\partial v}{\partial w} &=\frac{8}{\pi^{2}}\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right) \times \frac{h}{w^{2}+h^{2}} \\ \frac{\partial v}{\partial h} &=-\frac{8}{\pi^{2}}\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right) \times \frac{w}{w^{2}+h^{2}} \end{aligned}
DIoU損失を用いたNMS
DIoUは、損失関数としてではなく、NMSのためのスコアとしても使用できる。通常IoUがスコアとして使用されるところを、2つの矩形の中心間の正規化された距離である\mathcal{R}_{D I o U}=\frac{\rho^{2}\left(\mathbf{b}, \mathbf{b}^{g t}\right)}{c^{2}}を用いて、スコアは以下のように定義できる。
s_{i}= \begin{cases}s_{i}, & \operatorname{IoU}-\mathcal{R}_{D \operatorname{IoU}}\left(\mathcal{M}, B_{i}\right)<\varepsilon \\ 0, & \operatorname{IoU}-\mathcal{R}_{D I o U}\left(\mathcal{M}, B_{i}\right) \geq \varepsilon\end{cases}
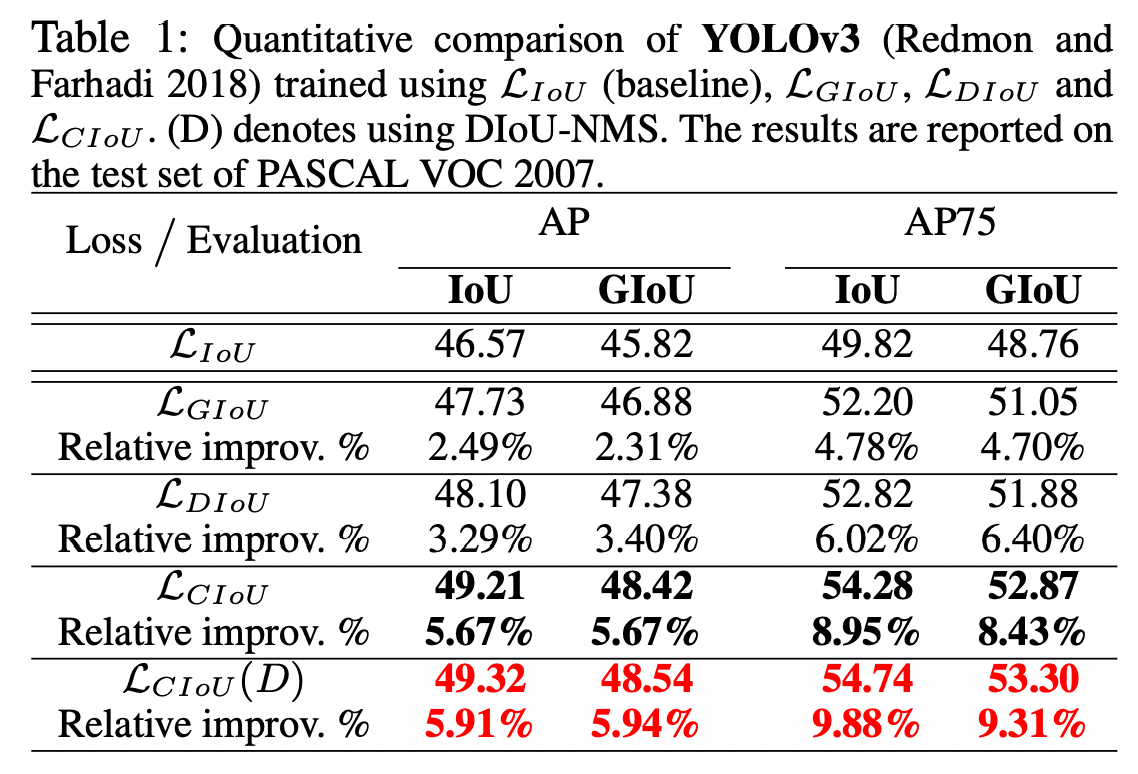
このDIoU-NMSは、実験では一貫して最終的な精度を向上させている。




Discussion