【論文5分まとめ】conditional invertible neural networks

概要

双方向の可逆な関数を表すInvertible Neural Network(INN)を条件付きにするConditional INN(cINN)を提案。以下は、本手法をColorizationに適用した例で、Conditionとしてモノクロ画像を使用し、さまざまなありそうな色合いの画像を生成している。

書誌情報

• Ardizzone, Lynton, et al. "Guided image generation with conditional invertible neural networks." arXiv preprint arXiv:1907.02392 (2019).
• https://arxiv.org/abs/1907.02392

ポイント

affine coupling blockの基礎

INNの代表格であるaffine coupling blockでは、入力をチャネル方向に分割し、分割された出力を算出する順方向の計算を以下のように行う。

$$v1=u1⊙exp⁡(s1(u2))+t1(u2)v2=u2⊙exp⁡(s2(v1))+t2(v1) \begin{aligned} &\mathbf{v}_{1}=\mathbf{u}_{1} \odot \exp \left(s_{1}\left(\mathbf{u}_{2}\right)\right)+t_{1}\left(\mathbf{u}_{2}\right) \\ &\mathbf{v}_{2}=\mathbf{u}_{2} \odot \exp \left(s_{2}\left(\mathbf{v}_{1}\right)\right)+t_{2}\left(\mathbf{v}_{1}\right) \end{aligned}$$

同じ$s1,s2,t1,t2s_1, s_2, t_1, t_2$を用いて、逆方向の計算は以下のように行える。逆関数が、複雑な計算なしに行えることがポイントである。

$$u2=(v2−t2(v1))⊘exp⁡(s2(v1))u1=(v1−t1(u2))⊘exp⁡(s1(u2)). \begin{aligned} &\mathbf{u}_{2}=\left(\mathbf{v}_{2}-t_{2}\left(\mathbf{v}_{1}\right)\right) \oslash \exp \left(s_{2}\left(\mathbf{v}_{1}\right)\right) \\ &\mathbf{u}_{1}=\left(\mathbf{v}_{1}-t_{1}\left(\mathbf{u}_{2}\right)\right) \oslash \exp \left(s_{1}\left(\mathbf{u}_{2}\right)\right) . \end{aligned}$$

conditional affine coupling block

affine coupling blockを$f(x;θ)f(\mathbf{x} ; \theta)$で表すとき、特定の条件に応じて変化するConditional Affine Coupling Block(CC)を関数$f(x;c,θ)f(\mathbf{x} ; \mathbf{c}, \theta)$で表す。CCでは、$s,ts, t$を条件付きの関数にすることでこれを実現する。例えば、$s1(u2)s_{1}\left(\mathbf{u}_{2}\right)$を$s1(u2,c)s_{1}\left(\mathbf{u}_{2}, \mathbf{c}\right)$に置き換える。CCは以下のような構造になる。

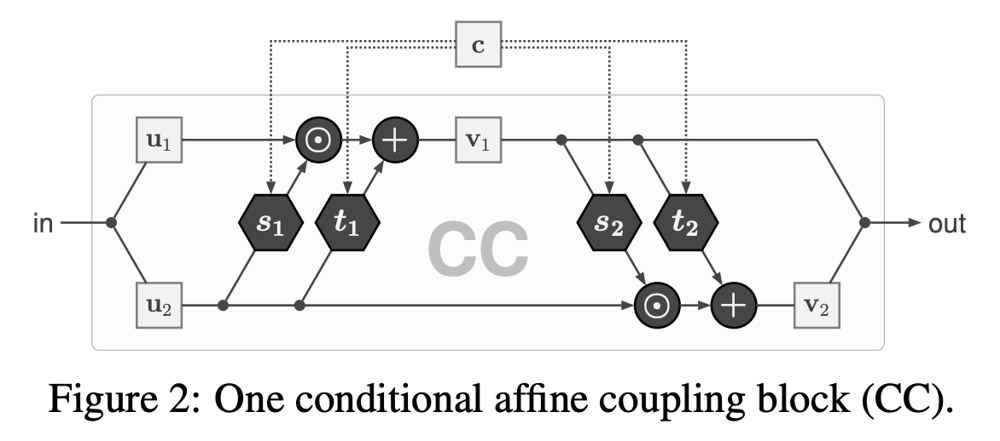
$ff$の逆関数$gg$は、以下のようになる。条件$c\mathbf{c}$は順方向でも逆方向でも同じように使用される。

$$f−1(⋅;c,θ)=g(⋅;c,θ) f^{-1}(\cdot ; \mathbf{c}, \theta)=g(\cdot ; \mathbf{c}, \theta)$$

最尤損失によるcINNの訓練

cINNは、最尤損失を用いて簡単に訓練できることを示す。

$pZ(z)p_{Z}(\mathbf{z})$を潜在空間$ZZ$における確率密度分布とする。$θ\theta$をパラメータ、$c\mathbf{c}$を条件とする関数$f(x;c,θ)f(\mathbf{x} ; \mathbf{c}, \theta)$を考える。この関数は全単射であり、以下のような変数変換が成り立つ。

$$pX(x;c,θ)=pZ(f(x;c,θ))∣det⁡(∂f∂x)∣ p_{X}(\mathbf{x} ; \mathbf{c}, \theta)=p_{Z}(f(\mathbf{x} ; \mathbf{c}, \theta))\left|\operatorname{det}\left(\frac{\partial f}{\partial \mathbf{x}}\right)\right|$$

$∂f∂x\frac{\partial f}{\partial \mathbf{x}}$はヤコビアンであり、そのサンプル$xi\mathbf{x}_i$における行列式を$Ji≡det⁡(∂f/∂x∣xi)J_{i} \equiv \operatorname{det}\left(\partial f /\left.\partial \mathbf{x}\right|_{\mathbf{x}_{i}}\right)$とする。

ベイズの定理により、$p(θ;x,c)∝pX(x;c,θ)⋅pθ(θ)p(\theta ; \mathbf{x}, \mathbf{c}) \propto p_{X}(\mathbf{x} ; \mathbf{c}, \theta) \cdot p_{\theta}(\theta)$が成り立つ。そのため、事後確率$p(θ;x,c)p(\theta ; \mathbf{x}, \mathbf{c})$を最大化したい時の損失関数は、以下のようになる。

$$L=Ei[−log⁡(pX(xi;ci,θ))]−log⁡(pθ(θ)) \mathcal{L}=\mathbb{E}_{i}\left[-\log \left(p_{X}\left(\mathbf{x}_{i} ; \mathbf{c}_{i}, \theta\right)\right)\right]-\log \left(p_{\theta}(\theta)\right)$$

ここで、$pX(x;c,θ)p_{X}(\mathbf{x} ; \mathbf{c}, \theta)$を先の式の右辺で置き換えると、以下のように書ける。

$$L=Ei[−log⁡(pZ(f(x;c,θ))−log⁡∣Ji∣]−log⁡(pθ(θ)) \mathcal{L}=\mathbb{E}_{i}\left[-\log \left( p_{Z}(f(\mathbf{x} ; \mathbf{c}, \theta)\right) -\log \left|J_i\right| \right]-\log \left(p_{\theta}(\theta)\right)$$

通常、$pZ(z)p_{Z}(\mathbf{z})$は標準ガウス分布を考え、$pθ(θ)p_{\theta}(\theta)$にもガウス分布が事前分布として与えられる。$1/2σθ2≡τ1 / 2 \sigma_{\theta}^{2} \equiv \tau$として、以下のように全体を書き直せる。

$$L=Ei[∥f(xi;ci,θ)∥222−log⁡∣Ji∣]+τ∥θ∥22 \mathcal{L}=\mathbb{E}_{i}\left[\frac{\left\|f\left(\mathbf{x}_{i} ; \mathbf{c}_{i}, \theta\right)\right\|_{2}^{2}}{2}-\log \left|J_{i}\right|\right]+\tau\|\theta\|_{2}^{2}$$

この式は、第1項は最大尤度損失で、第2項はL2正則化である。つまり、一般的に知られる通り、事後確率最大化は、正則化項付きの最尤法とも言える。

このような損失関数によって訓練されたネットワークのパラメータ$θ^ML\hat{\theta}_{\mathrm{ML}}$があれば、$z∼pZ(z)\mathbf{z} \sim p_{Z}(\mathbf{z})$と、ある$c\mathbf{c}$を用いて、条件付きの逆関数$g:xgen =g(z;c,θ^ML)g: \mathbf{x}_{\text {gen }}=g\left(\mathbf{z} ; \mathbf{c}, \hat{\theta}_{\mathrm{ML}}\right)$が得られる。

Conditioning Network

条件付き画像生成モデルでは、条件がone-hotベクトルのような単純な形になることもあるが、画像が条件となることもある。その場合は、分類タスクなどで学習されたネットワーク$hh$を用いて、$c~=h(c)\tilde{\mathbf{c}}=h(\mathbf{c})$をcINNへの入力とする。

その他の工夫

• $x\mathbf{x}$へのノイズ追加とデータ拡張が必要。特に、MNISTのような画像中の大部分がフラットな領域の場合はスパースな勾配になることが多いため。

• scaleを担当する$ss$に、以下のような非線形関数を追加する。これによって、$∣s∣≪α|s| \ll \alpha$のとき$sclamp ≈ss_{\text {clamp }} \approx s$になり、$∣s∣≫α|s| \gg \alpha$のとき$sclamp ≈±αs_{\text {clamp }} \approx \pm \alpha$になるため、$exp⁡α\exp{\alpha}$が爆発するのを防ぐ。

$$sclamp =2απarctan⁡(sα) s_{\text {clamp }}=\frac{2 \alpha}{\pi} \arctan \left(\frac{s}{\alpha}\right)$$

• Xavier Initializationで初期化することで、訓練が安定することを確認した。
• チャネル間の情報を交換するためのランダムに作られた直行行列を適用する。この行列は、訓練対象ではなく、一度作成したら固定する。これにより、$u1,u2\mathbf{u}_{1}, \mathbf{u}_{2}$の間の情報交換を効率的に行える。
• 以下のようなHaar waveletパターンを用いて、効率的に可逆なサイズ縮小を行う。Real NVPではチェッカーボードパターンを用いてこれをおこなっていたが、Haar waveletパターンを用いることで、average poolingと3方向への勾配情報も抽出しつつ、可逆性も確保することができる。

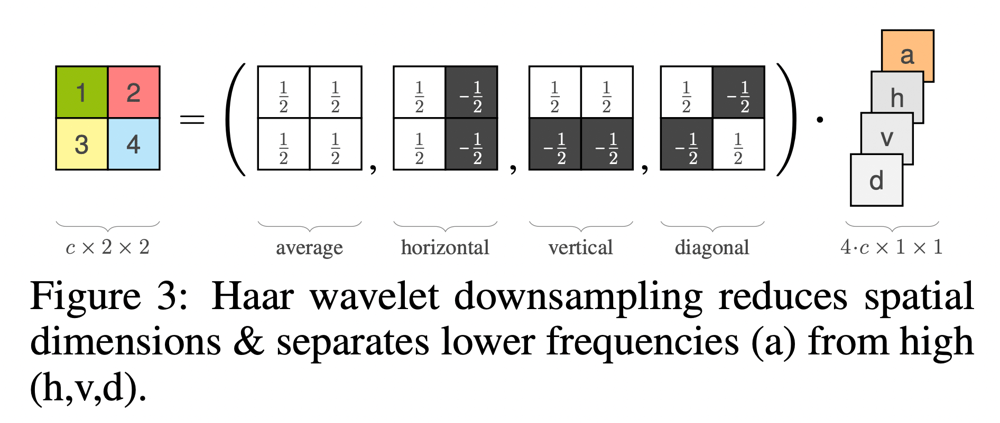
実験

省略