概要
深層学習モデルの量子化手法の一つ。量子化手法は、量子化の対象として重み、活性化、勾配を量子化する手法に大別されるが、本研究で提案しているPACTは活性化(Activation)を対象としている。大きな精度劣化なく活性化を量子化することに成功している。
書誌情報
- Choi, Jungwook, et al. "Pact: Parameterized clipping activation for quantized neural networks." arXiv preprint arXiv:1805.06085 (2018).
- https://arxiv.org/abs/1805.06085
ポイント
PACT
手法の肝となる部分は、非線形活性化関数ReLUを以下のような活性化関数で置き換えることである。この活性化関数は、ReLUの上限を\alphaでクリップしている形になる。\alphaは学習可能なパラメータであり、\ell_2正則化によって極端に大きな値を取らないように最適化される。
y=\operatorname{PACT}(x)=0.5(|x|-|x-\alpha|+\alpha)= \begin{cases}0, & x \in(-\infty, 0) \\ x, & x \in[0, \alpha) \\ \alpha, & x \in[\alpha,+\infty)\end{cases}
PACTによって、活性化のダイナミックレンジがある程度に抑えられることが期待され、量子化の際に妥当なスケールを選択できる。以下は、kbit量子化の場合に、PACTの出力である活性化が2^k-1以下のkbit整数値とスケール\frac{\alpha}{2^{k}-1}に分解できることを示している。
y_{q}=\operatorname{round}\left(y \cdot \frac{2^{k}-1}{\alpha}\right) \cdot \frac{\alpha}{2^{k}-1}
勾配は以下のように求めることができ、\alphaは通常のbackpropagationによって最適化できる。
\frac{\partial y_{q}}{\partial \alpha}=\frac{\partial y_{q}}{\partial y} \frac{\partial y}{\partial \alpha}= \begin{cases}0, & x \in(-\infty, \alpha) \\ 1, & x \in[\alpha,+\infty)\end{cases}
\alphaのメカニズム
PACTにおける\alphaは学習可能なパラメータであるが、ネットワーク全体で同じものを使うべきか、各レイヤーで独立させた方が良いのかを実験によって決めている。
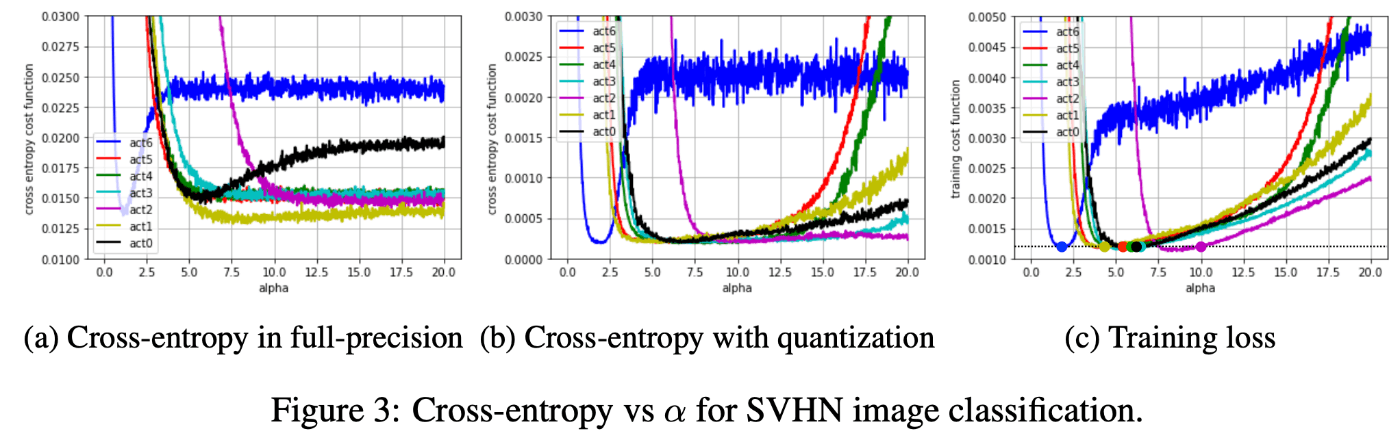
下図は各レイヤーに関して、それ以外の重みと\alphaを固定したときに、該当レイヤーの\alphaを変化させたときに損失がどのように変化するのかを示したグラフである。(a)は活性化を量子化しない場合のCE損失、(b)は活性化を量子化した場合のCE損失、(c)は活性化を量子化した時のCE損失+正則化損失を表している。
注目すべき点は2つある。1つ目は、量子化をしない場合は\alphaが大きくなっても損失が平坦になっていくのに対し、量子化をする場合は損失が平坦にならず、どんどん大きくなっていっているということである。このことは、量子化においてはスケールをコントロールするパラメータ(ここでは\alpha)がモデルの精度を大きく左右することを表している。2つ目は、各レイヤーによって損失が最も小さくなる位置が異なる、つまり最適な\alphaは異なっているという点である。
以上の実験から、PACTでは各レイヤーに独立した\alphaを設けている。
実験
実験については詳細は省く。以下の3つの実験をおこなっている。
- 活性化を量子化した場合の各種データセット、ネットワークに関する精度の比較をおこなっている。PACTはいずれのケースでも精度の劣化を小さくできることを示す実験をおこなっている
- 続けて、重みもDoReFaによって量子化し、PACTと組み合わせても問題ないことを示す実験をおこなっている
- 最後に、重みと活性化を量子化することで、固定小数点数のmultiply-and-accumulate unit(MAC unit)上でをResNet50を高速化できる例を示している



Discussion