Zenn
🐶

【論文5分まとめ】DAFNe

2022/02/01に公開
回転物体検出
tech

概要

1stageのアンカーフリー回転物体検出手法であるDAFNeを提案している。

書誌情報

ポイント

ネットワーク構造

DAFNeのネットワーク構造を下図に示す。Backbone, Feature Pyramid, Headの3部分からなる。BackboneはResNet50のような標準的なCNNを採用し、Feature Pyramidでは、さまざまな解像度の特徴マップを構築し、各解像度で共通の重みを持つHeadが接続される。

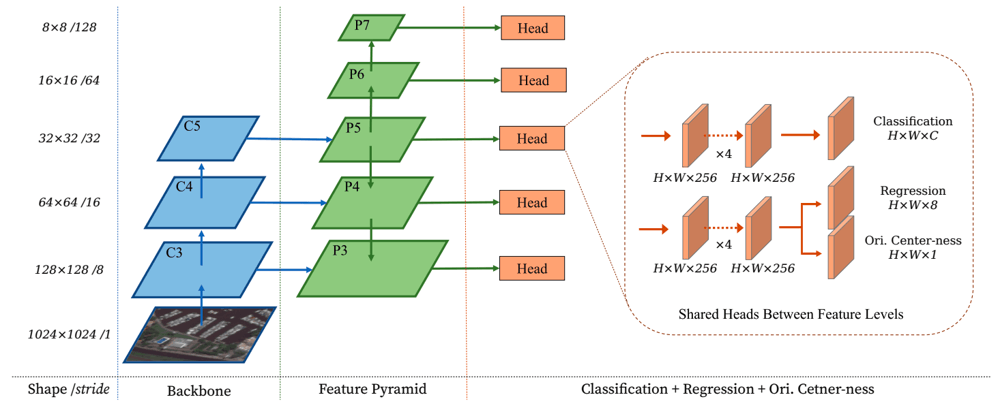
Headは特徴マップのピクセルごとに3つの予測を行う。

  • クラス分類
  • Box回帰
  • Oriented Center-ness

Oriented Center-ness

Center-nessは物体の中央らしさを表す数値で、アンカーフリーの物体検出手法として著名なFCOSで導入された。

DAFNeでは、訓練時のターゲットとなるCenter-nessを下図の(b)のようにすることで、Center-nessを回転物体検出でも使えるように一般化する。

回転矩形の4辺までの距離をa, b, c, dとすると、center-nessは以下のように定義される。\alphaは減衰率を表し、データセットによって最適な値が変わるので、チューニングが必要なハイパーパラメータである。実験では2~4までの値が使用されている。

\text { center-ness }(a, b, c, d)=\left(\frac{\min (a, c)}{\max (a, c)} \cdot \frac{\min (b, d)}{\max (b, d)}\right)^{\frac{1}{\alpha}}

推論時には、Center-ness o_{x, y}は、クラス分類の出力p_{x,y}と組み合わせて、最終的なスコアs_{x,y}を得るために使用される。

s_{x, y}=\sqrt{p_{x, y} \cdot o_{x, y}}

頂点の求め方

Regressionのターゲットは自明ではなく、以下の4つのパターンを検討している（下図）。

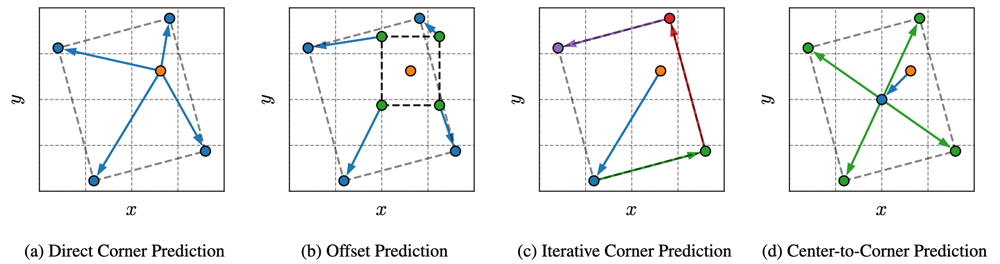
結論としては、(d)の矩形の中心までのベクトルと、中心から各頂点までのベクトルを求めるという戦略が最も安定して良い結果が得られたとしている。
この場合、中心までのベクトルを求める追加のチャネルが必要になる。

\begin{aligned} \tilde{\boldsymbol{c}} &=\text { center-branch }_{256 \rightarrow 2}(\boldsymbol{X}) \\ \boldsymbol{c}_{0}, \boldsymbol{c}_{1}, \boldsymbol{c}_{2}, \boldsymbol{c}_{3} &=\text { corner-branch }_{256 \rightarrow(4 \times 2)}(\boldsymbol{X})+\tilde{\boldsymbol{c}} \end{aligned}

損失関数

クラス分類はFocal Loss、Center-nessにはBinary cross-entropy Loss、RegressionにはSmoothed L1 Lossが用いられる。
特に、Regressionに関しては、訓練を安定化させるために、以下のようなeight point Lossが使用される。

\ell_{m r}^{8 p}=\min \left\{\begin{array}{l} \sum_{i=0}^{3}\left(\left|x_{(i+3) \% 4}-x_{i}^{*}\right|+\left|y_{(i+3) \% 4}-y_{i}^{*}\right|\right) \\ \sum_{i=0}^{3}\left(\left|x_{i}-x_{i}^{*}\right|+\left|y_{i}-y_{i}^{*}\right|\right) \\ \sum_{i=0}^{3}\left(\left|x_{(i+1) \% 4}-x_{i}^{*}\right|+\left|y_{(i+1) \% 4}-y_{i}^{*}\right|\right) \end{array}\right.

実験

3つのデータセットHRSC2016、DOTA 1.0/1.5について実験をおこなっている。
DOTAではSOTAを更新し、HRSCについては特化した手法であるPIoUに匹敵する精度を実現している。

Discussion