【論文5分まとめ】Deep Hough-Transform Line Priors

この記事は、論文の内容を5分くらいで読めるようにまとめた記事です。そのため、前提となる知識や関連研究に関する説明は大幅に省略しています。
基本的には筆者の備忘録ですが、面白そうと思ったら是非ご自身でも読んでみてください。

概要

微分可能なHough変換と逆Hough変換を実現するモジュールHT-IHT Blockを提案している。本研究がメインとしているタスクはワイヤーフレームの推定であり、とくに教師データが少ない時のPriorとして機能することが具体的な実験によって示されているが、本稿では特定のタスク向けの詳細は省略する。

書誌情報

• Lin, Yancong, Silvia L. Pintea, and Jan C. van Gemert. "Deep hough-transform line priors." European Conference on Computer Vision. Springer, Cham, 2020.
• ECCV2020
• https://arxiv.org/abs/2007.09493
• 公式実装

ポイント

Recap: Hough変換の流れ

画像中のある直線は、Houghドメインの特定の$(\rho, \theta)$と対応づけられる。この直線上の点$(x, y)$は、パラメータ$i$を用いて、以下のように表される。

$$(x(i), y(i))=(\rho \cos \theta-i \sin \theta, \rho \sin \theta+i \cos \theta)$$

• $\rho$は画像座標系の原点から直線までの最短距離（垂線の長さ）であり、0から画像の対角線の長さまでの値をとりうる。
• $\theta$は画像座標系の原点から直線までの垂線の角度であり、$0$以上$\pi$未満の値をとりうる。
• $\rho, \theta$のとりうる値は離散値で、本手法では$\rho$は183分割、$\theta$は60分割（3度おき）される。

画像中の座標$(x, y)$が属するHoughドメインでの座標$(\rho, \theta)$は、画像サイズが一定であれば常に同じで、この対応関係はサイズが$\left[W, H, N_{\rho}, N_{\theta}\right]$のバイナリマップ$\mathbf{B}$で表される。

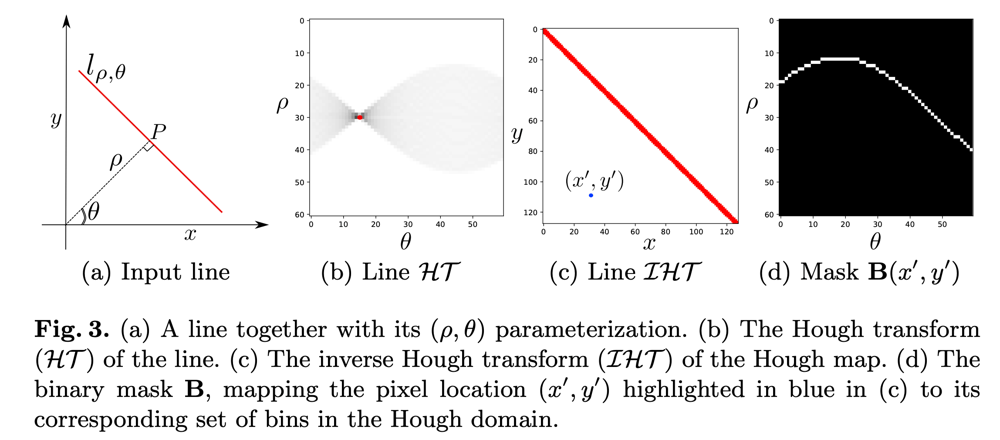
以上のような対応づけによるHoufh変換の流れを図示すると以下のようになる。

• (a)は入力画像中の線分を表し、この直線上の点$(x, y)$の数が$(\rho, \theta)$に投票される
• (b)はHoughドメインにおける投票数を表し、投票数が非常に多い点以外を抑制すると、赤い1点が得られる。
• (c)はHoughドメインにおいて支配的だった点に対応する直線を表す。
• (d)は、(c)におけるある点$(x', y')$のバイナリマップを表し、$(x', y')$を通る直線に対応する$(\rho, \theta)$のみが1その他が0というマップになっている。

HT-IHT Block

本研究では、$\mathcal{HT, IHT}$を特徴マップのそれぞれのチャネルに対して適用する、HT-IHT Blockを提案している。
本手法では、投票の重みとして入力された特徴マップ$\mathbf{F}$のactivationを用いる。

$$\mathcal{H} \mathcal{T}(\rho, \theta)=\sum_{i} \mathbf{F}_{\rho, \theta}(x(i), y(i))$$

バイナリマップ$\mathbf{B}$を用いると、Houghドメインの出力$\mathcal{HT}$は以下のように、簡潔に表現できる。

$$\mathcal{H T}=\mathbf{F B}$$

一方、逆Hough変換は、下式によって行われる。ここで、$N_{\theta}$はアングル$\theta$の数（60）である。

$$\mathcal{I} \mathcal{H T}(x, y)=\frac{1}{N_{\theta}} \sum_{\theta} \mathcal{H} \mathcal{T}(x \cos \theta+y \sin \theta, \theta)$$

Hough変換と同様に、$\mathbf{B}$を用いて完結に表現できる。

$$\mathcal{I} \mathcal{H} \mathcal{T}=\mathbf{B}\left(\frac{1}{N_{\theta}} \mathcal{H} \mathcal{T}\right)$$

論文中で使われている$N_{\theta}$のような正規化に使用している値は、公式実装を見てみると、HT・IHTともにやや異なるので、実装する際は安定する方法を試行錯誤した方がよさそうです。

一般的なHough変換では、Houghドメインで支配的な点のみを抽出することが多い。似たようなフィルタリング機能を、本手法では1次元Conv層によって実現する。

$\mathcal{HT}$に対して、カーネルサイズ9の1次元Conv層を適用しており、最初にdepthl-wise conv, その後通常のカーネルサイズ9の1次元Conv層が続き、活性化関数としてReLUを使用している。

実験

HT-IHT Blockが標準的な2次元Conv層よりも優れていることを確認するため、簡単なダミーデータによる実験を行っている。
この実験の目的は、ダミーデータに対する高精度なモデルを構築することではない。出力が直線のみから構成されるというPriorを、HT-IHTによって表現できることを確認することを目的としている。

下図の一番左の画像が入力された時に、直線の要素である2列目の画像を出力できるかを、3種類の非常に薄いネットワークで比較している

• Local-only：3x3Conv -> ReLUのみ
• Global-only：$\mathcal{HT}$-> 3x1Conv -> ReLU -> $\mathcal{IHT}$
• Local+Global：Global-onlyの出力を元の入力画像に対して掛ける。これにより無限に続く直線ではなく、線分に限定できる。

Local+Globalがもっとも良いAverage Precisionを達成でき、HT-IHT Blockによって3x3Convよりも直線要素を綺麗に抽出できることが確認できている。