概要
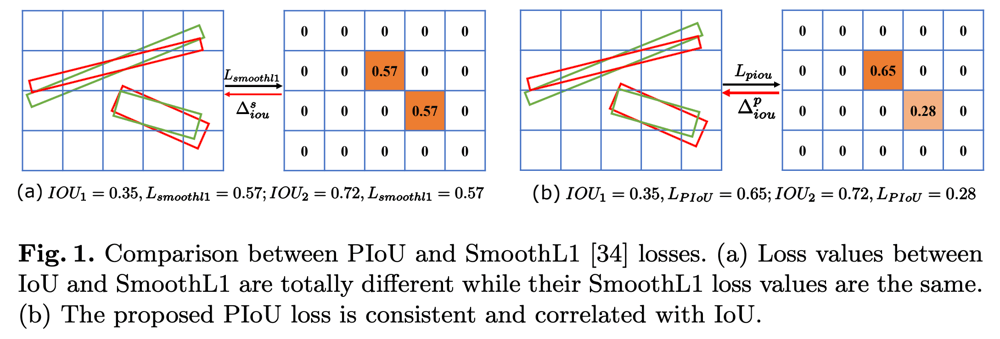
以下の図の(a)に示すように、回転矩形を予測するモデルの損失関数として使用される、Smooth L1損失が同じであっても、IoUは大きく異なるということがあり得る。これは、矩形のアスペクト比が大きい時に大きな問題となる。本研究では、(b)に示す、回転矩形同士のIoUを近似的に計算するPIoU(Pixel IoU)と、それを元にした微分可能な損失関数を提案している。
書誌情報
- Chen, Zhiming, et al. "Piou loss: Towards accurate oriented object detection in complex environments." European Conference on Computer Vision. Springer, Cham, 2020.
- https://arxiv.org/abs/2007.09584
ポイント
PIoUの定義
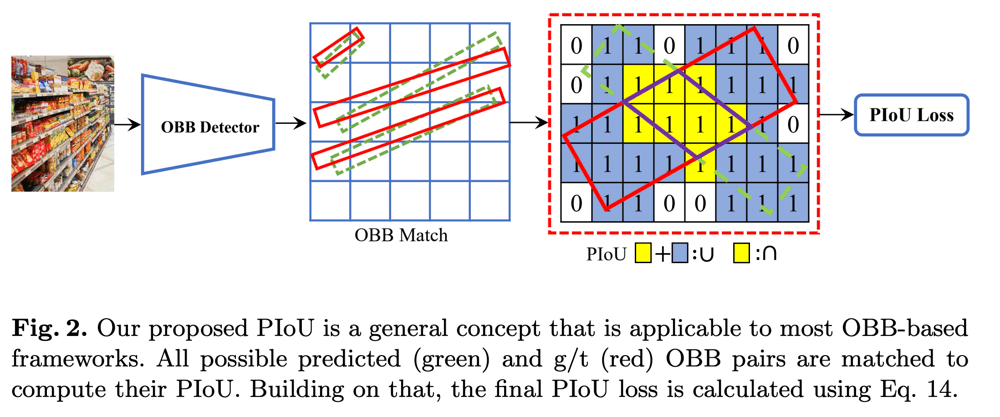
2つの回転矩形間のIoUは、通常やや複雑な計算が必要である。PIoUは、矩形内に含まれているピクセルの数を元にIoUを計算する方法である。下図の例では、PIoUの分子は黄色いピクセルの数で、分母は黄色と青のピクセルの総数である。
ピクセル\boldsymbol{p}_{i, j}が回転矩形\boldsymbol{b}に含まれているかを判定する\delta\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}\right)を以下のように定義する。ここで、d_{i,j}^w, d_{i,j}^hやw, hは以下の図のように定義される。
\delta\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}\right)= \begin{cases}1, & d_{i, j}^{w} \leq \frac{w}{2}, d_{i, j}^{h} \leq \frac{h}{2} \\ 0, & \text { otherwise }\end{cases}
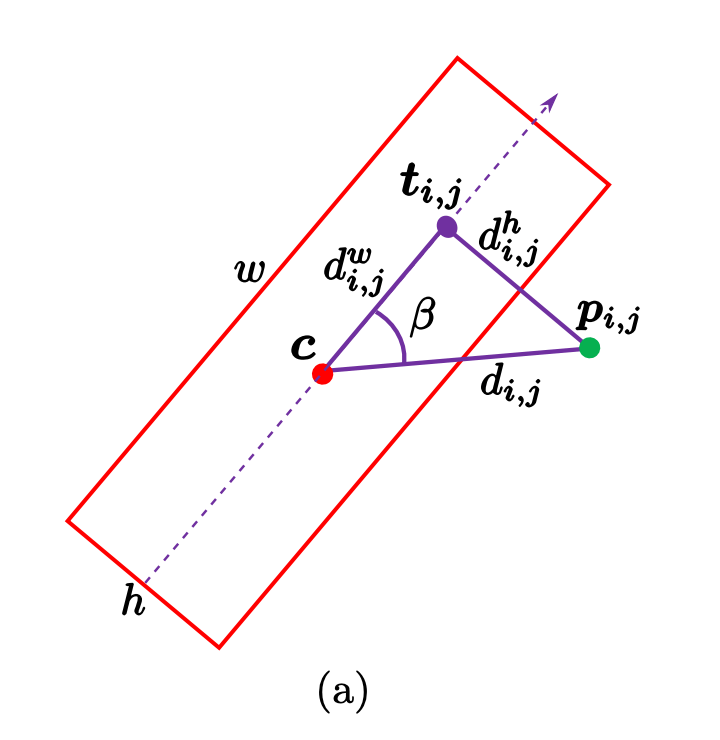
\begin{aligned} d_{i j} &=d(i, j)=\sqrt{\left(c_{x}-i\right)^{2}+\left(c_{y}-j\right)^{2}} \\ d_{i j}^{w} &=\left|d_{i j} \cos \beta\right| \\ d_{i j}^{h} &=\left|d_{i j} \sin \beta\right| \\ \beta &= \begin{cases}\theta+\arccos \frac{c_{x}-i}{d_{i j}}, & c_{y}-j \geq 0 \\ \theta-\arccos \frac{c_{x}-i}{d_{i j}}, & c_{y}-j<0\end{cases} \end{aligned}
予測回転矩形\boldsymbol{b}と真の回転矩形\boldsymbol{b}^{\prime}を囲む最小の水平矩形をB_{\boldsymbol{b}, \boldsymbol{b}^{\prime}}とおくと、2つの回転矩形に共に含まれるピクセルの数S_{\boldsymbol{b} \cap \boldsymbol{b}^{\prime}}といずれかに含まれるピクセルの数S_{\boldsymbol{b} \cup \boldsymbol{b}^{\prime}}は以下のように書ける。
\begin{gathered} S_{b \cap b^{\prime}}=\sum_{\boldsymbol{p}_{i, j} \in B_{b, b^{\prime}}} \delta\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}\right) \delta\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}^{\prime}\right) \\ S_{\boldsymbol{b} \cup \boldsymbol{b}^{\prime}}=\sum_{\boldsymbol{p}_{i, j} \in B_{b, b^{\prime}}} \delta\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}\right)+\delta\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}^{\prime}\right)-\delta\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}\right) \delta\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}^{\prime}\right) \end{gathered}
以上からPIoUは、\text{PIoU}_{\boldsymbol{b}, \boldsymbol{b}^{\prime}}=\frac{S_{\boldsymbol{b} \cap \boldsymbol{b}^{\prime}}}{S_{\boldsymbol{b} \cup \boldsymbol{b}^{\prime}}}と求めることができる。しかし、このように求めたPIoUは微分不可であり、直接損失関数として使用するのは望ましくない。
微分可能なPIoU
PIoUを微分可能にするために、非連続な関数\delta\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}\right)を近似する微分可能な関数を以下のように考える。
F\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}\right)=K\left(d_{i, j}^{w}, w\right) K\left(d_{i, j}^{h}, h\right)
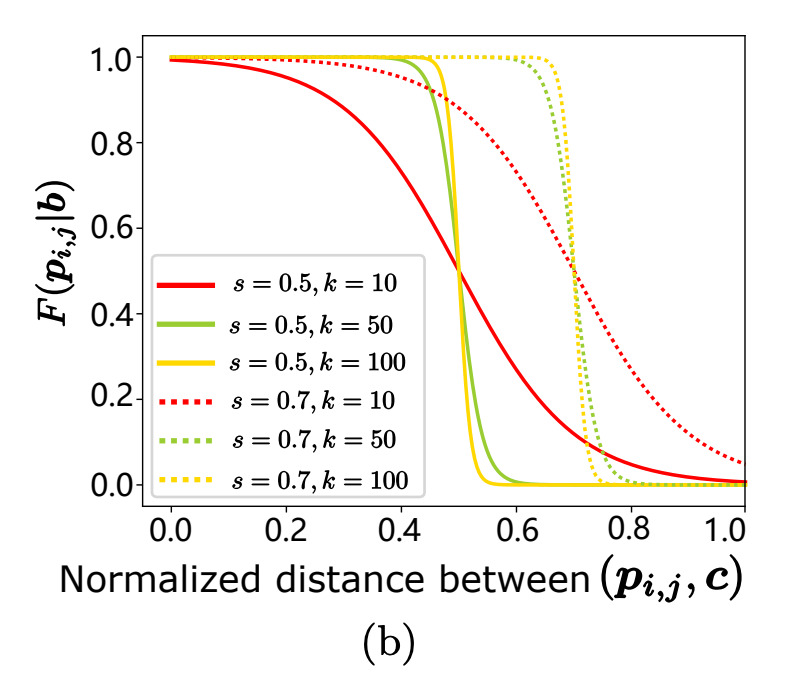
ここで、カーネル関数K(d, s)=1-\frac{1}{1+e^{-k(d-s)}}を用いることで、F\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}\right)は微分可能になる。kは下図のように、大きくすることでよりステップ関数\delta\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}\right)に近づけることができるパラメータであり、実験の結果k=10付近が適当であるとされている。
このような近似を用いることで、S_{\boldsymbol{b} \cap \boldsymbol{b}^{\prime}}とS_{\boldsymbol{b} \cup \boldsymbol{b}^{\prime}}の微分可能な近似が以下のように得られる。
\begin{gathered} S_{b \cap b^{\prime}} \approx \sum_{\boldsymbol{p}_{i, j} \in B_{b, b^{\prime}}} F\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}\right) F\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}^{\prime}\right) \\ S_{b \cup \boldsymbol{b}^{\prime}} \approx \sum_{\boldsymbol{p}_{i, j} \in B_{b, b^{\prime}}} F\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}\right)+F\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}^{\prime}\right)-F\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}\right) F\left(\boldsymbol{p}_{i, j} \mid \boldsymbol{b}^{\prime}\right) \end{gathered}
なお、S_{b \cup b^{\prime}}は上式のように律儀に求めることもできるが、以下のように簡略化したバージョンも考えられる。この場合はやや精度は劣化するが、訓練時間が若干短縮されることが実験によって示されている。
S_{b \cup b^{\prime}}=w \times h+w^{\prime} \times h^{\prime}-S_{b \cap b^{\prime}}
以上のようなPIoUを用いて、PIoU損失は以下のように定義できる。Mは(\boldsymbol{b}, \boldsymbol{b}^{\prime})のペアの数で、アンカーベースの手法だと、事前に定義されているアンカーのうち、真の回転矩形とのIoUが一定値以上あるものの数である。
L_{\text {piou }}=\frac{-\sum_{\left(\boldsymbol{b}, \boldsymbol{b}^{\prime}\right) \in M} \ln \operatorname{PIoU}\left(\boldsymbol{b}, \boldsymbol{b}^{\prime}\right)}{|M|}
PIoU損失は、通常の水平矩形間の損失関数としても使用でき、2つの矩形間に重なりがなくても微分可能な損失が発生するという点でGIoU損失のような特性を持っている。
実験
本研究では、回転物体検出のための特殊なデータセットとして、Retail50K Datasetも提案している。これは、小売店舗の棚を検出するという1クラスの回転物体検出データセットになっている。下の図のような棚を検出することが目標となる。アスペクト比が非常に大きいことがわかる。

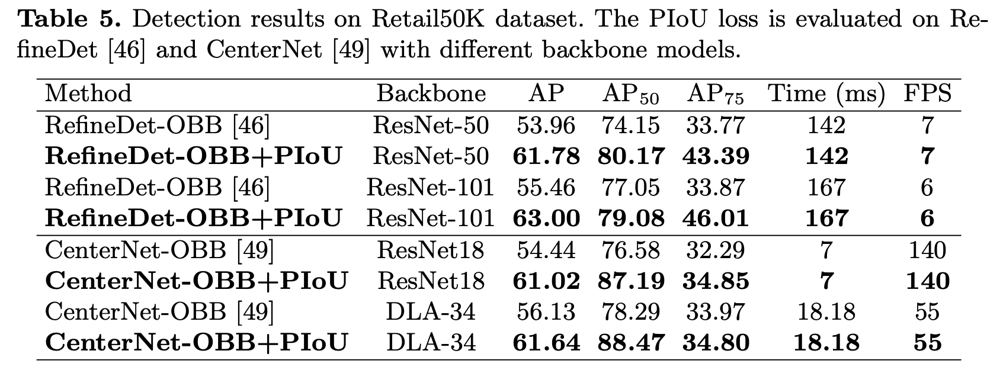
以下の表は、Retail50Kに関する評価を表しており、既存の回転物体検出手法にSmooth L1損失の代わりにPIoU損失を導入することで精度が大きく向上することを示している。







Discussion