Zenn
🐶

【論文5分まとめ】Deep Supervised Hashing Based on Stable Distribution

2021/12/21に公開
#
画像検索
tech

概要

画像検索のために画像特徴量をバイナリ化するDeepHashの一手法であるDSHSDを提案。既存の手法を大きく上回る性能を達成。

書誌情報

ポイント

前提となるネットワーク構造を以下に示す。このネットワーク構造である理由は、既存手法との比較のためであり、特徴抽出を行うネットワーク構造は何でも良い。

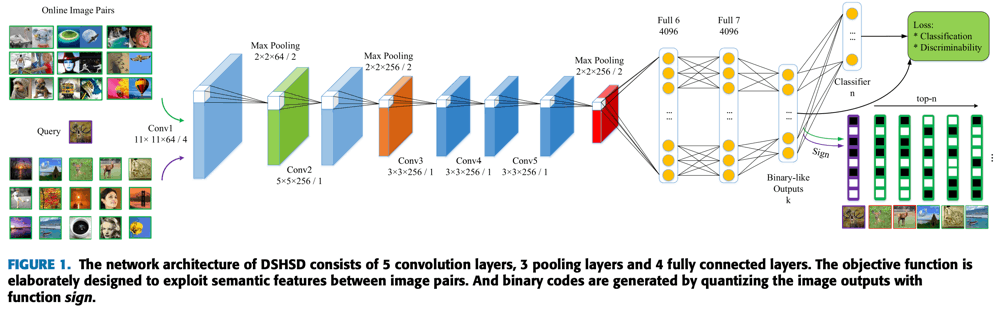
重要なのは、出力付近にあるLinear層とSign操作によるバイナリ化、および損失である。

処理の流れ

入力画像\boldsymbol{I}_{i}から画像特徴\boldsymbol{x}_{i} \in \mathbf{R}^kを抽出する。kはハッシュの長さを表すビット数である。

\boldsymbol{x}_{i}=\boldsymbol{W}_{d}^{T} \Phi\left(\boldsymbol{I}_{i} ; \theta\right)+\boldsymbol{v}_{d}

訓練時は\boldsymbol{x}_iにさらに線形変換が施され、分類損失が計算される。
推論時は\boldsymbol{x}_iの符号である\boldsymbol{b}_{i}=\operatorname{sign}\left(\boldsymbol{x}_{i}\right)\in\{+1,-1\}^{k}を得られる。これにより、得られたハッシュを用いることで、ハミング距離が近い画像を探索することで画像検索が実現できる。

損失関数

訓練時に使用する損失関数は、理想的には以下のような形で考えられる。

\begin{aligned} L_{d}(\mathcal{B}, \mathcal{S})=\sum_{s_{i j} \in \mathcal{S}}\left\{\frac { 1 } { 2 } \left(1-s_{i j}\right)\left\|\boldsymbol{b}_{i}-\boldsymbol{b}_{j}\right\|_{2}^{2} + \frac{1}{2} s_{i j} \max \left(0, m-\left\|\boldsymbol{b}_{i} - \boldsymbol{b}_{j}\right\|_{2}^{2}\right)\right\} \end{aligned}
  • \mathcal{S}は画像\boldsymbol{I}_{i}と\boldsymbol{I}_{j}が類似（画像同士が同じクラスに属する）していれば0, そうでなければ1となるように対応づけられた行列である。
  • mはマージンを表し、十分にバイナリコードが離れていないと損失が発生するようにしている。マージンmはビット数kの2倍の値が採用されている。

しかし、この損失関数は、離散化操作が途中にあることにより最小化が難しい。そこで、既存の手法では、\mathcal{X}に量子化正則化\left\|\boldsymbol{x}_{i}-\operatorname{sign}\left(\boldsymbol{x}_{i}\right)\right\|_{2}^{2}を施すことで最適化の問題を回避している。

量子化正則化は一見よさそうに思えるが、画像特徴量\mathcal{X}の分布形状を大きく変える方向に作用してしまう。下図の(a)は分類損失のみで訓練した時の\mathcal{X}の分布、(b)は量子化正則化を加えた時の分布を表す。きれいな単峰が崩れてしまい、訓練に悪影響を及ぼすことが知られている。

このような問題を回避するために、本研究ではStable分布という概念を導入している。厳密な定義は論文中に記載されているが、要するに、単峰の分布を保てるように、\boldsymbol{b}_{i}=\operatorname{sign}\left(\boldsymbol{x}_{i}\right)の代わりに\boldsymbol{h}_{i}=\tanh \left(\boldsymbol{x}_{i}\right)を使用して、最初に示した損失関数を最小化しよう、というものである。

\begin{aligned} L_{d}(\mathcal{H}, \mathcal{S})=\sum_{s_{i j} \in \mathcal{S}}\left\{\frac { 1 } { 2 } \left(1-s_{i j}\right)\left\|\boldsymbol{h}_{i}-\boldsymbol{h}_{j}\right\|_{2}^{2} +\frac{1}{2} s_{i j} \max \left(0, m-\left\|\boldsymbol{h}_{i}-\boldsymbol{h}_{j}\right\|_{2}^{2}\right)\right\}\end{aligned}

実際、このような損失関数に変更することで、\mathcal{X}の分布は上図の(c)のように保たれることが確認できている。なお、(d)は\mathop{tanh}{X}の分布を表している。

最終的な損失関数は以下のようになる。分類損失L_cは\mathcal{H}=\mathop{tanh}(\mathcal{X})をLinear層に入力し、その出力を用いて計算される。\alphaは2つの損失のバランスを取るための係数。

L(\mathcal{Y}, \mathcal{S}, \mathcal{H})=L_{c}+\alpha L_{d}

実装は簡単

非公式実装を見てみるとわかるが、DSHSDは以下のとおり非常にシンプルに実装できる。

DSHSD
class DSHSDLoss(torch.nn.Module):
    def __init__(self, config, bit):
        super(DSHSDLoss, self).__init__()
        self.m = 2 * bit
        self.fc = torch.nn.Linear(bit, config["n_class"], bias=False).to(config["device"])

    def forward(self, u, y, ind, config):
        u = torch.tanh(u)

        dist = (u.unsqueeze(1) - u.unsqueeze(0)).pow(2).sum(dim=2)
        s = (y @ y.t() == 0).float()

        Ld = (1 - s) / 2 * dist + s / 2 * (self.m - dist).clamp(min=0)
        Ld = config["alpha"] * Ld.mean()
        o = self.fc(u)
        if "nuswide" in config["dataset"]:
            # formula 8, multiple labels classification loss
            Lc = (o - y * o + ((1 + (-o).exp()).log())).sum(dim=1).mean()
        else:
            # formula 7, single labels classification loss
            Lc = (-o.softmax(dim=1).log() * y).sum(dim=1).mean()

        return Lc + Ld

実験

詳細は省く。

  • CIFAR-10, NUS-WIDE, ImageNetで検索し、TopNのPrecisionの平均値であるMAPで評価している。
  • CIFAR-10での実験から\alphaは0.1程度が良いという結果が得られている。
  • ビット数kは、12, 24, 32, 48-bitで評価している。
  • 既存の手法と比較し、安定して高いMAPが得られることを確認している。

Discussion