[Package] Optim.jlを使って最尤推定 | コイン・多項ロジット

まえがき

最尤推定法 (maximum likelihood method) は機械学習における基本的なアプローチとして頻出します．細かい話は置いておくとして，観測したデータから尤度関数 $L(\theta)$ やその対数 $\log L(\theta)$ を最大化するような $\theta^\star_\mathrm{MLE}=\arg\max \log L(\theta; \text{observed data }\mathcal{D})$ を推定値とするアプローチです．そのため対数尤度関数 $\log L(\theta)$ の微分などの情報を利用して推定を行います．

最尤推定 | コインの例

例題

よくある例題です．コインを振って表が出る確率を$\theta$，裏が出る確率を$1 - \theta$とします．全部で$N$回コインを適当に投げ，そのうち$r$回表が出た場合を考えると，$\theta$に対してこの事象が起きた確率を計算すると

$$L(\theta) := {}_{N}\mathrm{C}_{r} \theta^r (1 - \theta)^{N - r}$$

となります．最尤推定法ではこれを最大化する $\theta$ を推定値とします．ここでは $L(\theta)$ もしくは $\log L(\theta)$ を直接微分して $=0$ とすることで，推定値は $\hat{\theta} = \frac{r}{N}$ となります．

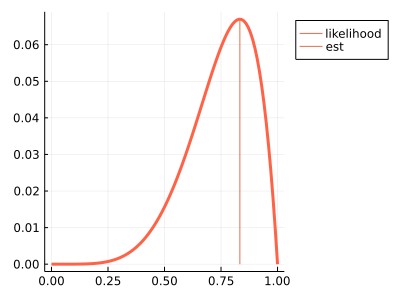
Julia Plots.jlを用いた確認

ここでは$L(\theta)$が平易な形をしているので，実際に$\theta$の関数としてプロットして確かめましょう．ここで ${}_{N}\mathrm{C}_{r}$ は定数部分なので省略しています．

using Plots
gr()

Lterm(x; N=6, r=5) = x ^ r * (1 - x) ^ (N - r);

N, r = 6, 5
xseq = 0:0.01:1.0;
yseq = Lterm.(xseq);
f = plot(size=(400, 300), legend=:outertopright)
plot!(f, xseq, yseq, color=:tomato, lw=3, label="likelihood")
plot!(f, [r/N, r/N], [0, Lterm(r/N)], label="est")
f

Julia Optim.jlを利用した推定

今回は閉じた式 $\hat{\theta} = \frac{r}{N}$ で推定できますが，ここで最適化用のライブラリOptim.jlを利用してみます．Optim.jlは最適化する関数$f$を受け取り様々な最適化手法で関数を最小化する $x^\star=\arg\min f(x)$ を計算します．そこで上の対数尤度関数 $\log L(\theta)$ を最大化する $\theta$ を求めてみます．最大化問題に対応するために符号を反転させることと，Optim.jlで与える関数はベクトルを引数につけとる関数にする必要があるので (不正確な日本語かもしれません)，1変数関数の場合でも x ではなく x[1] のように数値を与えます．

以下が実装です．対数尤度の計算で $\log(\cdot)$ の引数に負の値が入ると死亡するため，ここでは探索範囲を $[0.0001, 1.0]$ とし，初期値は$0.5$です．求まった値は $x_m = 0.8333333$ で，$N=6, r=5$の場合の推定値とほぼ一致しました．

using Optim
using Plots
gr()

# 対数尤度関数 Optim.jl 用
LL(q; N=6, r=5) = -(log(N) + r * log(q[1]) + (N - r) *log(1 - q[1]))

# Optim.jlで最適値を求める
res = optimize(LL, [0.0001], [1.0], [0.5])
xm = Optim.minimizer(res)[1];

# 描画
xseq = 0:0.01:1.0;
yseq = LL.(xseq);
f = plot(size=(400, 300), legend=:outertopright)
plot!(f, xseq, yseq, color="tomato", lw=3, label="log-likelihood")
plot!(f, [xm, xm], [0.0, LL(xm)], lw=5, label="min")
f

最尤推定 | 意思決定における多項ロジットの例

離散選択モデル (いくつかの候補が離散的に与えられ，そのうち1つを選ぶ) は意思決定の基本的なモデルとして経済学 (計量経済学) などを中心に広く使われています． 理論的な背景は書籍やインターネット上の文書にお願いするとし，ここでは簡単な例だけを考えます．数式の詳細は置いておくとして，$J$個の選択肢から$j$を選択する確率はパラメータ$\{\beta_j\}$と，入力特徴$\{x_j\}$が同じく$J$次元で与えられるとして

$$P(j\text{を選択}; \{x_j\}_{j=1}^{J}) = \frac{\exp(\beta_j x_i)}{\sum_{k} \exp(\beta_k x_k)}$$

で計算するというもので，ニューラルネットワークなどを日々扱っている人には馴染みの深い計算かと思います．この場合の観測データとしては，$x_j$という特徴量の人は$y_j$を選択した，というデータになります．パラメータ$\beta_j$の部分が未知になっていて，データが推定することで与えられた選択データセットのユーザの選択嗜好を推定するというのがやりたいことです．

例題

ここで例題を用いて具体的な例を使って計算をしてみます．例題は参考文献から取ってきています．ユーザが適当にいたとして選択肢として$J=\{1,2\}$を考えます (例題では「1がバスを選択する行為」「2が自家用車を選択する行為」です)．それぞれの選択肢をとったときの効用 (これは意思決定問題における嬉しさを定量化したものだと思ってください) として，入力属性値 $\{t_1, t_2, c_1, c_2\}$ の式として決定的に

$$V_1(t_1, t_2, c_1, c_2) = \alpha t_1 + \beta c_1$$

$$V_2(t_1, t_2, c_1, c_2) = \alpha t_2 + \beta c_2 + \gamma$$

の式で書かれていると仮定します．このときいろんな人の選好が混じっており，同じ$(t_1, t_2, c_1, c_2)$ の値であっても$1$を選択する場合と，$2$を選択する場合が確率的に発生するとします．そのため，観測したデータから入力属性毎に$1$と$2$を選択した回数をカウントし (コインの表が出た回数を $N$回中$r$回とカウントしたように)，データとしておきます．この確率的な選択モデルにおいて，データからパラメータ $\alpha, \beta, \gamma$を推定したいというのが最尤推定法のやりたいことです．

参考文献から拝借してきたデータは次の表です．

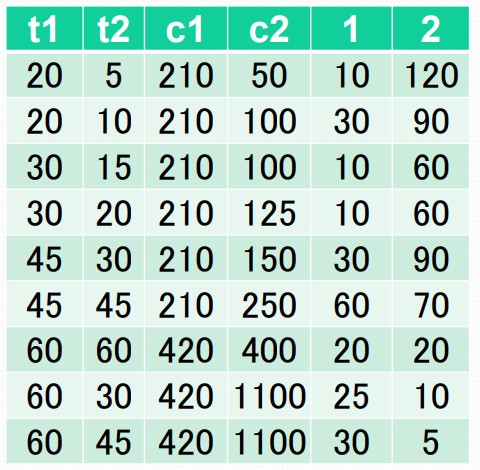
計算

上のモデルにおいて$J=2$のため，確率$P_1$と$P_2$は次の式で計算されます．

$$P_1(t_1, t_2, c_1, c_2; \alpha, \beta, \gamma) = \frac{\exp(\alpha t_1 + \beta c_1)}{\exp(\alpha t_1 + \beta c_1) + \exp(\alpha t_2 + \beta c_2 + \gamma)}$$

$$P_2(t_1, t_2, c_1, c_2; \alpha, \beta, \gamma) = 1 - P_1(t_1, t_2, c_1, c_2; \alpha, \beta, \gamma)$$

今データに値 $(t_1, t_2, c_1, c_2)$ とそれぞれの洗濯回数 $n_{1}, n_{2}$ が記録されているので，対数尤度関数はそれをすべて足し合わせたものです．これを最尤推定すると，参考文献のExcelを用いた結果によると，

$$\hat\alpha=-0.06449, \hat\beta=-0.00454, \hat\gamma=0.231912$$

になるとのことです．

Julia Optim.jlを利用した推定

雑に実装します (真似しないでください)．今回は$\alpha, \beta, \gamma$の3次元関数なのでそのまま実装してOKです．

using Optim
using Plots
gr()

# データ
data = [
    20 5 210 50 10 120;
    20 10 210 100 30 90;
    30 15 210 100 10 60;
    30 20 210 125 10 60;
    45 30 210 150 30 90;
    45 45 210 250 60 70;
    60 60 420 420 20 20;
    60 30 420 1100 25 10;
    60 45 420 1100 30 5
]

# 効用と確率
V1n(x, α, β) = α * x[1] + β * x[2];
V2n(x, α, β, γ) = α * x[1] + β * x[2] + γ;
P1n(x, α, β, γ) = exp(α * x[1] + β * x[2]) / (exp(α * x[1] + β * x[2]) + exp(α * x[3] + β * x[4] + γ));

# 対数尤度 (最小化問題にするために-符号)
function LL(param)
    α, β, γ = param
    ll = 0.0
    for row in eachrow(data)
        p1n = P1n([row[1] row[3] row[2] row[4]], α, β, γ)
        p2n = 1 - p1n
        l1 = row[5] * log(p1n)
        l2 = row[6] * log(p2n)
        ll += l1 + l2
    end
    -ll
end

# Optim.jlで最小化
res = optimize(eval, [0.0, 0.0, 0.0], autodiff=:forward, LBFGS())

# 出力
α, β, γ = Optim.minimizer(res)
println(α)
println(β)
println(γ)
println(LL(Optim.minimizer(res)))

特に終了条件などをいじらず適当に使ったOptim.jlの計算によれば

$$\tilde\alpha=-0.063433, \tilde\beta=-0.00454, \tilde\gamma=0.24903$$

となりました．Excelの結果と少し異なりますが，だいたいうまく動いたと思って良さそうですね．

参考文献

• Optim.jlについては公式のドキュメントを参照しました: https://julianlsolvers.github.io/Optim.jl/stable/#
• 多項ロジットの数値例についてはこちらのスライドから拝借しました: http://bin.t.u-tokyo.ac.jp/startup14/file/2-1.pdf
• 他には世の中の説明などを参考しました: https://h-memo.com/logit-model/