Zenn
👋

[Package] Turing.jlでベイズモデリング

2021/12/15に公開
Julia
#
ベイズ
tech

Twitter芸人名@cocomoffです．

この記事はJulia Advent Calendar 2021の15日目の記事です．18日目にも別ネタで書く予定です．この記事ではTuring.jlと呼ばれるパッケージを利用したベイズモデリングを簡単に説明して，Stanと比較をしてみたいと思います．ベイズモデリング自体は朝倉書店から出版されている豊田さんの「実践ベイズモデリング―解析技法と認知モデル―」の例題を使っています．

ベイズモデリングとは何か

本を読みましょう (!?)．

もしくは適当なスライドを見ましょう．

簡単な例題 | ゆがんだコインを振る

もしベイズモデリングとゆがんだコインの関係が知りたい場合には，例えばQiitaの記事を見てください．

理想的なコインを投げる場合，表と裏が出る確率がそれぞれ\frac{1}{2}というのは良い(?)と思います．ここでは歪んだコイン (もしくは表を出すのがすごいうまい人など)を考え，なんとなく表が出やすいコインを考えましょう (表の出る確率 p^\star=0.65，裏の出る確率 $1-p^\star=0.55%とします)．一般的な話は書籍などに譲るとして，Turing.jlを利用したアプローチを見ていきます．

歪んだコインを投げたデータを作る

歪んだコインは p^\star=0.65 となるベルヌーイ分布なので，JuliaではDistributions.jlを利用して簡単に100回振ることが出来ます．

using Distributions
using Turing
using StatsPlots

pstar = 0.65
coin = Bernoulli(pstar)
trial = 100 # 100回数振る
data = rand(coin, trial)

println("# of 表: $(sum(data))") # => 例えば57回
println("# of 裏: $(trial - sum(data))") # => 例えば43回

Turing.jlを使ったモデルの表現

Turing.jlを利用してモデルを考えていきます．パラメータp (真の値はp^\star=0.65) について，どういう気持ちを入れたいかと考えます．特に何も知らないという振りをしてコインの表が出る確率は \mathrm{Uniform}(0, 1) であると考えてもいいでしょう．一方ベイズ本を読んだことがある人がいれば，「ベルヌーイ分布の共役事前分布はベータ分布だ！」といった呪文 (もしくは真面目な式典解) を知っているかもしれません．ここではそれを入れ込んでTuring.jlのモデルを作ってみましょう．

@model function coin_model(data)
    p ~ Beta(1, 1) # pの事前分布はベータ分布
    N = length(data)
    for n in 1:N
        data[n] ~ Bernoulli(p) # データはgiven pのときのベルヌーイ分布に従う
    end
end

ちなみにこのコインの例はTuring.jlのQuick Startでも使われている話になります: https://turing.ml/dev/docs/using-turing/quick-start

Turing.jlを使った推論と結果

後はTuring.jlのサンプラさんを利用して，サンプル取得や描画をやってみます．

# サンプラの設定とサンプリング
iterations = 1000
ϵ = 0.05
τ = 10
chain = sample(coin_model(data), HMC(ϵ, τ), iterations)

#  描画
histogram(chain[:p])

描画を見てみます．

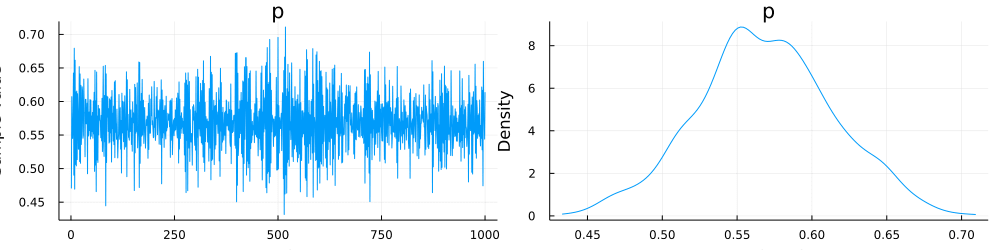
pの事後分布

100回降ったデータからpについて推測してみると0.55ぐらいと推測されている様子ですね．もう少しデータを増やして，2000回のコイン結果と，iterationsを10000ぐらいまで適当に大きくしてやってみます．

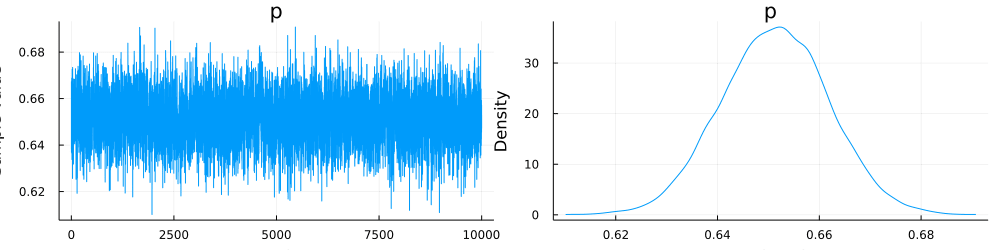
pの事後分布その2

このようにサンプラとデータをグッとしてあげると，なんとなく「p^\star=0.65あたりっぽいよね～」という推論が完成しました．詳しい使い方やサンプラの調整などについては，ドキュメントを見たり試行錯誤したりすると良いでしょう．

例題 (書籍§1.2) StanとTuring.jlの比較

極値データの扱いとして，ガンベル分布を用いたベイズモデリングを考えます．

走り幅跳びの記録として1991年から2015年の記録が与えられます (表1.2．後ほどJuliaのコードで出てきます) ．このとき，次のような研究上の問いを考えました (以下は書籍例題の一部引用です)．

  • RQ.1 男子走り幅跳びの各年の最長記録として最も出やすい記録 (最頻値) は何m何cmでしょうか．また最長記録の最頻値について，95%の革新で，どの程度の幅といえるでしょうか．

Stanの利用

このような例題に対するStanのモデル表現として，次のような計算がされています．

code11.stan
data { 
  int<lower=0> N;
  real<lower=0> x[N];
}
parameters {
  real<lower=0> mu;
  real<lower=0> sigma;
}

model {
  for (i in 1:N)
    x[i] ~ gumbel(mu, sigma);
}

generated quantities{
  real	s;          #SD
  real	p_w;        #世界記録は何パーセント点か
  real	x_99;       #99パーセント点
  real	u_rover100; #再現期間が100年より長い確率
  real	r_w;        #世界記録の再現レベル(1/再現期間)
  real	xpred;      #xの予測値
  real	p_new;      #予測値>8.95の確率
  s = sqrt(pow(pi(),2)*pow(sigma,2)/6);
  p_w = exp(-exp((mu-8.95)/sigma));
  x_99 = mu-sigma*(log(-log(0.99)));
  u_rover100 = 8.95>x_99 ? 1 : 0;
  r_w = 1/(1-exp(-exp((mu-8.95)/sigma)));
  xpred = gumbel_rng(mu,sigma);
  p_new = xpred>8.95 ? 1: 0;
}

簡単に解説します（Rは詳しくないので適当です）．詳しくは関連ドキュメントなどを読んで頂ければと思います (参考: Stanのブロック)

  • 1番目のブロックは，Rから入力されるデータに関する宣言部です．走り幅跳びの記録がN年分あり，それぞれのデータが配列x[0], x[1], \dotsに格納されるイメージです．
  • 2番目のブロックは分布のパラメータに関する部分です．今回の例ではガンベル分布を使うので，パラメータは，Wikipediaのページに従えば\muと\etaです (本では．\etaを\sigmaで書いているので，コードも\sigmaです)．
  • 3番目のブロックはベイズモデリングのモデルです．今回はデータx[i]がガンベル分布に従うという気持ちが書かれています．
  • 4番目のブロックがデータ解析で計算したい様々な数値です．サンプリングで推定したパラメータを利用して計算したい量を書きます．

Turing.jlの利用

ここでは書籍のデータをJuliaに持ってきて，そこからデータを読み込んで同じ推論を行います．Stanの方で，データやパラメータの_lower_などがありますが，これをTuring.jlに持ってくる方法があまりよく分からなかったので，適当に設定しています．

using Turing
using Distributions
using StatsPlots
using Plots
gr()

data = [] # ここに書籍のデータを入れる
N = length(data)

# モデルを書く
@model function jump(data)
    # ガンベル分布
    μ ~ Uniform(0.0, 10.0)
    σ ~ Uniform(0.0, 2.0)

    N = length(data)
    for n in 1:N
        data[n] ~ Gumbel(μ, σ)
    end
end

# サンプリング
iterations = 3000
chain = sample(jump(data), NUTS(), iterations)

# Stanのgenerated quantitiesを計算するために
# サンプリング後の推定値を使ってR/Stanのコードと同じ計算をする．

## 2つのパラメータμとσの推定値を適当に取ってくる
μbar = mean(chain[:μ]);
σbar = mean(chain[:σ]);

## Stanと同じ式を計算する
s = sqrt(π^2 * σbar^2 / 6) # 分散
pw = exp(-exp((μbar - 8.95) / σbar)) # 実現点
x99 = μbar - σbar * log(-log(0.99)) # 99%点
urover100 = 8.95 > x99 ? 1 : 0 # 再現期間が100年より長い確率
rw = 1 / (1 - exp(-exp((μbar - 8.95) / σbar))) # 再現期間

## 再現したパラメータによる予測分布
xpred = Gumbel(μbar, σbar)
plot(xpred, xlim=(8.0, 10.0), size=(300, 300), label=nothing)

予測分布と推定値の比較

推定後の予測分布を見てみます．

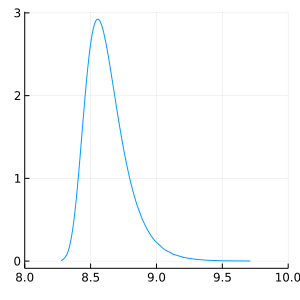
予測ガンベル分布

最後に書籍に載っていたRとStanを用いた推定値と，Turing.jlで計算した推定値を比較します．

書籍 (EAP) Turing.jl
\mu 0.8542 8.542
\sigma 0.121 0.122
s 0.155 0.156
p_{8.95} 0.963 0.965
x_{0.99} 9.100 9.103
1/r_{8.95} 38.519 28.797

雑ですが，だいたい使えたような気持ちになりました (一部ちゃんと見ていないですが…)．

まとめ

Stanで書かれているモデルでも，ほとんど似たような感じでTuring.jlを用いてベイズモデリング・推論できることが分かりました．

Discussion