Zenn
☂️

エノン写像の作図（非線形時系列解析の基礎理論 1章）

2023/05/03に公開
Julia
数値計算
tech

タイトルの通り「非線形時系列解析の基礎理論（amazonのページ / 東京大学出版会のページ）」という本をパラパラと読んでいます。1章で非線形時系列解析の歴史と発展が語られているのですが、エノン写像と呼ばれるものの図と例が出てきます。

https://ja.wikipedia.org/wiki/エノン写像

書籍に出てくる図のグラフを再現するプログラムをJuliaで書いて遊びたい、というのがこの記事の内容です。notebookはこちらにあります。

https://github.com/cocomoff/Visualize-HenonMap

系列を計算する

上のWikipediaのページでは力学系の例として2式で書かれています。

\begin{align} x_{n+1} &= 1 - a x^2_n + y_n \\ y_{n+1} &= bx_n \end{align}

書籍では簡単に1行で書かれています。

x_{t} = 1 - a x^2_{t-1} + bx_{t-2}

これをこのまま計算する関数を用意すれば良いです。もう少し真面目に書けばよかったかもしれません。雑に配列に格納しました。

function make_series(x1, x2; a=1.4, b=0.3, T=100)
    X = [x1, x2]
    for t in 1:T
        xt = 1 - a * X[end] ^ 2 + b * X[end-1]
        push!(X, xt)
    end
    X
end

Plots.jl を使って図を描くとこのようになります。

作図したもの

seq1 = make_series(0.1, 0.1; T=98);

f = plot(legend=:outertopright, size=(1000, 300), ylims=(-1.5, 1.5))
plot!(f, seq1, lw=1, color=:black, label="x1=0.1, x2=0.1, a=1.4, b=0.3")

系列の初期値依存性を見る

make_series にいろんな初期値や係数を与えると、初期値にどのように依存するかを確認できます。x_2 が 0.1 の場合と 0.1001 の場合で変化を観察してみます。

作図したものがこちらです。途中から違いが出てきますね。

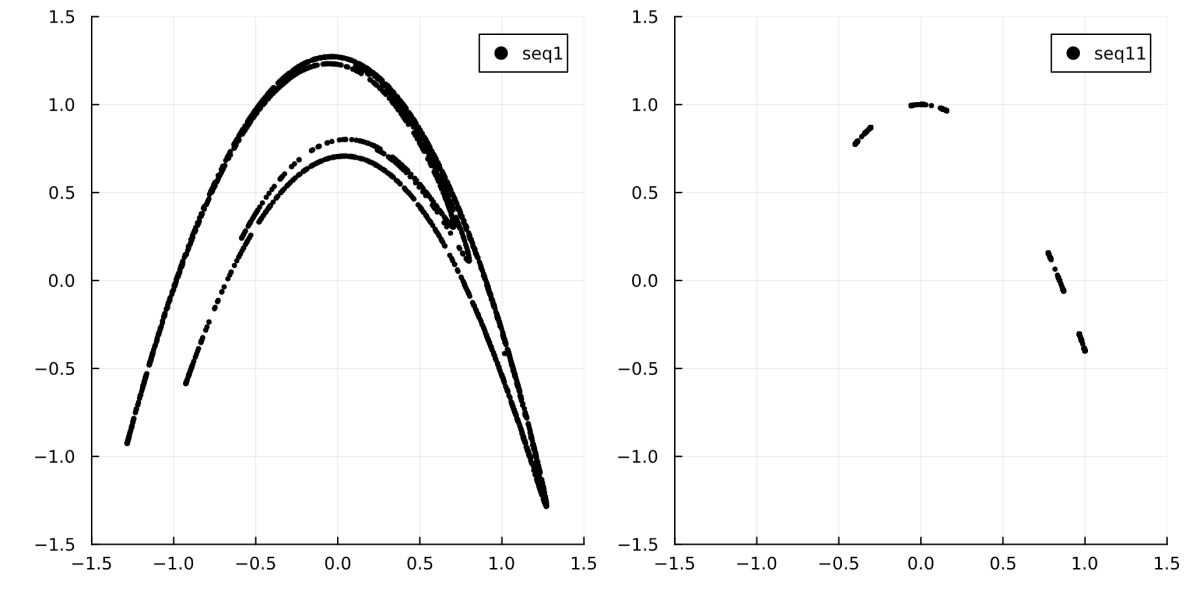
作図したもの

系列のリターンプロットを見る

横軸に x_t を、縦軸に x_{t+1} を取った図を作図してみます。時系列データが配列に格納されているので、インデクスをズラして散布図を描けば良いです。本の例を作図しました。

seq1 = make_series(0.1, 0.1; T=2000);
seq11 = make_series(0.1, 0.1; T=2000, b=0.0);

lims = (-1.5, 1.5)
f1 = scatter(seq1[3:end-1], seq1[4:end], size=(400, 400), ms=2, color=:black, xlims=lims, ylims=lims, label="seq1")
f2 = scatter(seq11[3:end-1], seq11[4:end], size=(400, 400), ms=2, color=:black, xlims=lims, ylims=lims, label="seq11")
plot!(f1, f2, size=(800, 400))

図が描けました。

作図したもの

分岐図を描く

変化させるパラメータを横軸に、過渡状態を取り除いた後に取る x_t の値を縦軸に描く作図をしてみます。「過渡状態を取り除く」の部分を、どう実装するべきかよく分からなかったので適当な実装をしたら、少しだけ角みたいなものが出ちゃいました（書籍にはない）。真面目に計算しないといけなかったかもしれません。

f = plot(size=(500, 500), ylim=(-1.5, 1.5))

# b=0.3で固定し、aの探索は0.0から1.5まで0.01刻みとする
T = 500
L = 100
for a in range(0.0, 1.5; step=0.001)
    seq_a = make_series(0.1, 0.1; a=a, b=0.3, T=T-2)
    
    # 長さTの系列から、末尾のLぐらいで取りうる値を取得する
    plot_y = collect(Set(seq_a[end-L:end]))
    plot_x = [a for _ in 1:length(plot_y)]
    
    scatter!(f, plot_x, plot_y, ms=1, color=:black, label=nothing)
end

f

そこそこの図が出来ました（ちょっと微妙なところもある）。

作図したもの

まとめ

作図してみると、いろいろ学びがありますね。また続きを読みたいと思います。

Discussion