審査員の点数を見ながら、いろんなランキングの順位相関係数を計算してみよう
採点競技で点数を付けたり、点数でランキングを作ったりして遊ぶことがあると思います。
例えば下の図はあるコンテストでの点数を表にしたものです(A〜Gが点数をつけた人、0〜9が点数を付けられた人です)。
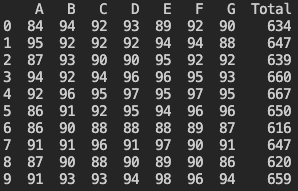
こういう遊びをしていると
- ある人の付けた点数のランキングって、どれぐらい結果に影響したの?
- ある人を除いたランキングってどういう感じだったの?
みたいなことを思うことがあると思います。
そこでこちらの記事では「順位相関係数」という道具を使って、上のデータを例にデータを少しだけ見てみようと思います。ここで使う道具は「スピアマンの順位相関係数」と呼ばれるものですが、詳しく興味のある方は世の中のサイトを確認してみてくださいね。
個人(A〜G)のランキングと全体のランキングの関係
やったこと
まずは個人の点数で付けたランキングが、全員の合計点数で付けたランキングにどれぐらい相関していたのかを見てみましょう。
まずは計算の対象(答え)となる全体のランキングですが、表の一番右側の列(Total)を見て、Totalの点数の大きい順に並べたものです。つまり5番目の人が667点で1位、4番目の人が660点で2位、という感じで並べれば良いですね。具体的には
というのが全体でのランキングになります。
次にある個人のつけたランキングを見てみましょう。同じ用に、各列(点数)を高い順に並び替えたものと比較すれば良いです。例えばAの人が付けたランキングは「2番目の人が95点で1位、4番目の人が94点で2位、…」といなっているので、(同じ点数の人の存在に目をつぶって並び順の小さい方が強いとする)ランキングでは
となります。本当はタイの点数を真面目に処理しないといけない気がします(誰か実装をお願いします)。
2つのランキング scipy.starts.spearmanrを使っています。計算すると、相関係数とp値が出力されます。
結果
結果は次のようになりました。結構ばらついていることが分かりますね。細かい説明を除いてp値を信じるとすると、ジャッジGはなかなかの相関を示していますね。負の相関係数が出るのは、それはそれで面白い結果だなと思います。
ジャッジA: -0.382 (p-value 0.2762553)
ジャッジB: 0.055 (p-value 0.8810362)
ジャッジC: 0.273 (p-value 0.4458383)
ジャッジD: 0.406 (p-value 0.2442823)
ジャッジE: 0.152 (p-value 0.6760652)
ジャッジF: 0.358 (p-value 0.3103761)
ジャッジG: 0.879 (p-value 0.0008139)
ある個人(A〜G)を取り除いた場合のランキングと全体のランキングの関係
やったこと
似たような処理ですが、逆に「ある人の点数がなかったらどうなるんだろう」というのを考えてみたいと思います。処理としては
- ある個人(A~G)を取り除いた残りの人の合計点数を出す
- 合計点数からランキングを作り、全体のランキングと比較する
とします。細かい処理は同じです。
結果
結果は次のようになりました。
ジャッジA以外: 0.127 (p-value 0.7260570)
ジャッジB以外: 0.564 (p-value 0.0897240)
ジャッジC以外: 1.000 (p-value 0.0000000)
ジャッジD以外: 0.515 (p-value 0.1275529)
ジャッジE以外: 0.952 (p-value 0.0000228)
ジャッジF以外: 0.661 (p-value 0.0375884)
ジャッジG以外: 0.661 (p-value 0.0375884)
結果を見てみると、ある個人のランキングとの順位相関係数を求めていた場合とガラッと異なる結果になっているように見えますね。1.000の数値が見えるのものがあって面白いですね。逆に言うと取り除くと相関が下がるということは…?みたいな考え方が出来るかも知れませんね。
まとめ
データを見てみるといろいろ考えることができますね(?)。
コードと参考のデータです。たぶんどこか間違ってると思いますので、真面目に読む方は気をつけてください。
Discussion