Zenn
Closed6

アルゴ式「動的計画法 2-3」を Swift で解く

Swift
#
競技プログラミング
#
動的計画法
小清水 健人小清水 健人

高階関数を使ったメモ化と再帰

次の関数によって、再帰呼び出しの結果をメモ化することができます。

func memo<T: Hashable, U>(body: @escaping(((T) -> U), T) -> U) -> (T) -> U {
    var memo = [T: U]()
    var function: ((T) -> U)!

    function = { x in
        memo[x] ?? {
            let r = body(function, x)
            memo[x] = r
            return r
        }()
    }
    return function
}

パラメータ body は (((T) -> U), T) -> U、戻り値は (T) -> U です。
body は漸化式を表していて、これを memo に渡すことでメモ化された関数に変換しています。

こちらの Qiita に掲載されている記事で丁寧に説明されています。
https://qiita.com/taka1068/items/ea1cb0d01f2e7cc67df7

WWDC 2014 の Advanced Swift が元ネタみたいです。35:30 頃に説明されています。
https://youtu.be/o_sKVMvSn_Q

小清水 健人小清水 健人

例：フィボナッチ数

メモ化と再帰の例として、フィボナッチ数を計算してみます。
フィボナッチ数は次の漸化式で定義されます。

F_0 = 0\\ F_1 = 1\\ F_i = F_{i-1} + F_{i-2} \space (i \ge 2)

これをメモ化関数によって、次のように実装することができます。

/// フィボナッチ数列
///
/// - `F(0) = 0`
/// - `F(1) = 1`
/// - `F(i) = F(i-1) + F(i-2)`
let fibonacci: (Int) -> Int = memo { F, i in
    switch i {
    case 0: // 第0項
        return 0

    case 1: // 第1項
        return 1

    case _: // 一般項
        return F(i-1) + F(i-2)
    }
}

関数 memo によって上述の漸化式は、計算済みの結果をキャッシュするため二度目の計算は高速です。たとえば、F(20) を計算する場合を考えますと、F(20) = F(19) + F(18) ですが、第二項 F(18) は 第一項 F(19) = F(18) + F(17) によって既に計算済みで、キャッシュを返すだけで実際には計算はされません。

60 番目のフィボナッチ数は次のようにして出力できます。

// 1548008755920
print(fibonacci(60))

20 番目までのフィボナッチ数は次のようにして出力できます。

// 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765
print(
    (0...20)
        .lazy
        .map(fibonacci)
        .map(String.init)
        .joined(separator: " ")
)
小清水 健人小清水 健人

インデックスが二次元の場合

メモ化関数はインデックスが Hashable であることを要求します。
これは計算済みの結果を、インデックスをキーとして辞書にキャッシュするためです。

今回は次のように定義しました。

struct Index: Hashable {
    let row: Int
    let column: Int
}

二次元の場合も一次元の漸化式と同様、インデックスの初期値まで再帰すれば問題を解くことが可能です。

小清水 健人小清水 健人

動的計画法 2-3 の問題を漸化式で表現する

i 日目に j の仕事に取り組んだとします。

i 日目までの報酬の合計は、i 日目の報酬と {i-1} 日目までの報酬の合計との和で表すことができます。
i 日目に j の仕事に取り組むと、当日は A_{i,j} の報酬を得ることができ、また、前日は j ではない仕事に取り組んでいるはずなので、次の等式が成り立ちます。

F_{i,j} = A_{i,j} + \max_{k \not = j} F_{i-1,k} \space \space \space ( i = 0, 1, ..., N-1, \space j = 0, 1, 2 )

ただし、0日目の場合は過去に遡ることはできないので合計ではなく0日目の報酬そのものです。

F_{0,j} = A_{0,j}

上述の内容を関数 memo によって実装すると次のようになります。

let dp: (Index) -> Int = memo { F, index in
    let (i,j) = (index.row, index.column)
    switch i {
    case 0: // 初項
        return aa[i][j]

    case _: // 一般項
        return aa[i][j] + max(
            F(Index(row: i-1, column: (j+1)%3)),
            F(Index(row: i-1, column: (j+2)%3))
        )
    }
}

ここで、 j = 0, 1, 2 なので、 (j+1)%3, (j+2)%3 は j と相異なる２数です。
aa は報酬を表す二次元配列です。

let N = Int(readLine()!)!
var aa = [[Int]]()
for _ in 0...N-1 {
    aa.append(readLine()!.split(separator: " ").map { Int(String($0))! })
}
小清水 健人小清水 健人

報酬の最大値を求める

N 日間の報酬の最大値を求めます。
最終日に仕事 0、仕事 1、仕事 2 を選んだ際のそれぞれの最大値を計算して、３パターンの報酬のうちで最大となる値が求めるべき値になります。

max(
    dp(Index(row: N-1, column: 0)),
    dp(Index(row: N-1, column: 1)),
    dp(Index(row: N-1, column: 2))
)

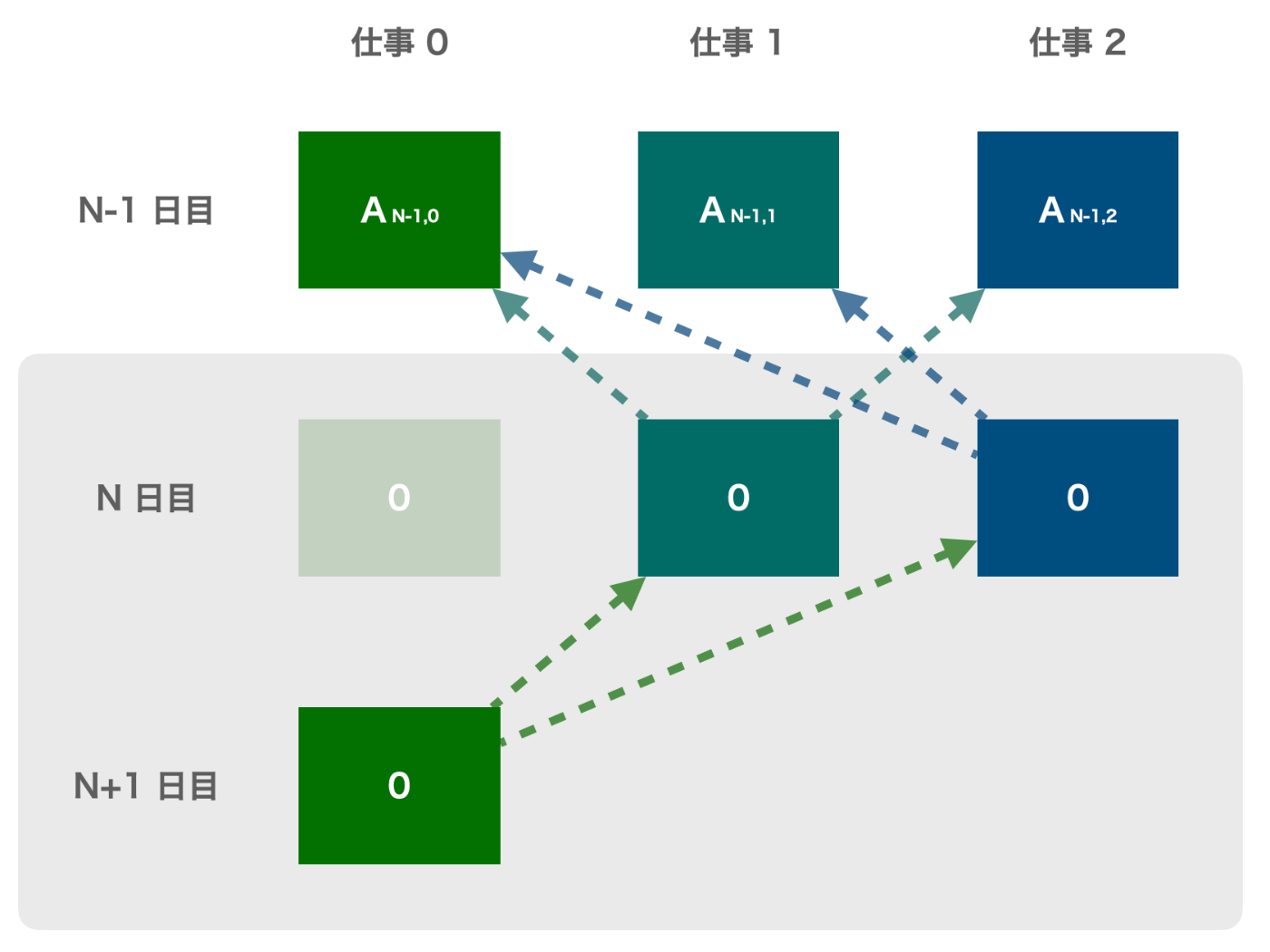
これが解答です。しかし、 N, N+1 日目に報酬量 0 の仕事を便宜上設定することで、dp の呼び出しを１度だけにすることもできます。N+1 日目の仕事 0 の最大値を求めることで、求めるべき値になります。

最終的な解答は以下になります。

func memo<T: Hashable, U>(body: @escaping(((T) -> U), T) -> U) -> (T) -> U {
    var memo = [T: U]()
    var function: ((T) -> U)!

    function = { x in
        memo[x] ?? {
            let r = body(function, x)
            memo[x] = r
            return r
        }()
    }
    return function
}

struct Index: Hashable {
    let row: Int
    let column: Int
}

let N = Int(readLine()!)!
var aa = [[Int]]()
for _ in 0...N-1 {
    aa.append(readLine()!.split(separator: " ").map { Int(String($0))! })
}
aa.append([0, 0, 0])
aa.append([0])

let dp: (Index) -> Int = memo { F, index in
    let (i,j) = (index.row, index.column)
    switch i {
    case 0: // 初項
        return aa[i][j]
    case _: // 一般項
        return aa[i][j] + max(
            F(Index(row: i-1, column: (j+1)%3)),
            F(Index(row: i-1, column: (j+2)%3))
        )
    }
}
print(dp(Index(row: N+1, column: 0)))
このスクラップは2021/08/29にクローズされました