【TeX】TikZで3次元空間を表現する方法

TikZというパッケージを用いてLaTeXで3次元空間を表現する方法について紹介します。Overleafで動作確認済みです。

本記事ではあくまで基本的な三次元空間を表現する方法についてのみ紹介しており、細かい部分を網羅はしておりません。

本記事のゴールは以下のような図形を作ることです。

スクリプト全体を見る

各行の説明は次セクション以降に記載しています。

\documentclass{article}
\usepackage{tikz}
\usepackage{tikz-3dplot}
\usetikzlibrary{math}
\usetikzlibrary{arrows.meta}

\begin{document}

\tdplotsetmaincoords{60}{135}
\begin{center}
\begin{tikzpicture}[scale=3, tdplot_main_coords]

    % 座標軸
    \draw[thick] (-0.5,0,0) -- (1.2, 0, 0);  % x軸
    \draw[thick] (0,-0.5,0) -- (0, 1.2, 0);  % y軸
    \draw[thick] (0,0,-0.4) -- (0, 0, 1.2);  % z軸

    % ベクトル r1, r2, r3
    \draw[->, ultra thick, >=Latex] (0, 0, 0) -- ({cos(20)}, {sin(20)}, 0);  % r1
    \draw[->, ultra thick, >=Latex] (0, 0, 0) -- ({-sin(20)}, {cos(20)}, 0);  % r2
    \draw[->, ultra thick, >=Latex] (0, 0, 0) -- (0, 0, 1);  % r3

    % ベクトル e1, e2, e3
    \draw[->, ultra thick, >=Latex] (0, 0, 0) -- (1, 0, 0);  % e1
    \draw[->, ultra thick, >=Latex] (0, 0, 0) -- (0, 1, 0);  % e2
    \draw[->, ultra thick, >=Latex] (0, 0, 0) -- (0, 0, 1);  % e3

    % 点線
    \draw[dashed, thick, dash pattern=on 1pt off 1pt] ({cos(20)}, 0, 0) -- ({cos(20)}, {sin(20)}, 0);
    \draw[dashed, thick, dash pattern=on 1pt off 1pt] (0, {sin(20)}, 0) -- ({cos(20)}, {sin(20)}, 0);
    \draw[dashed, thick, dash pattern=on 1pt off 1pt] ({-sin(20)}, 0, 0) -- ({-sin(20)}, {cos(20)}, 0);
    \draw[dashed, thick, dash pattern=on 1pt off 1pt] (0, {cos(20)}, 0) -- ({-sin(20)}, {cos(20)}, 0);

    % ラベル
    \node at (1.4, 0, 0) {\textbf{$x$}};
    \node at (0, 1.4, 0) {\textbf{$y$}};
    \node at (0, 0, 1.4) {\textbf{$z$}};
    \node at ({1.1*cos(20)}, {1.1*sin(20)}, 0) {$\mathbf{r}_1$};
    \node at ({-1.1*sin(20)}, {1.1*cos(20)}, 0) {$\mathbf{r}_2$};
    \node at (0.2, 1, 0) {$\mathbf{e}_2$};
    \node at (1.1, 0, 0.1) {$\mathbf{e}_1$};
    \node at (0.1, -0.1, 1) {$\mathbf{e}_3 = \mathbf{r}_3$};
    \node at (0.1, -0.1, 1) {$1$};
    \node at (1.1, 0.1, 0) {$1$};
    \node at (-0.1, 1.1, 0) {$1$};

    % 回転角度 γ
    \draw[thick] (0.3, 0, 0) arc[start angle=0, end angle=20, radius=0.3];
    \node at (0.5, 0.1, 0) {$\gamma$};
    \draw[thick] (0, 0.3, 0) arc[start angle=90, end angle=110, radius=0.3];
    \node at (0.1, 0.5, 0) {$\gamma$};

\end{tikzpicture}
\end{center}

\end{document}

プリアンブルについて

まず、TikZと3次元描画用のライブラリを読み込む必要があります。
プリアンブルに以下を追加してください。

\usepackage{tikz}
\usepackage{tikz-3dplot} % 3次元描画をサポートするためのライブラリ
\usetikzlibrary{math} % tikz内で数値計算を行う際に必要なライブラリ
\usetikzlibrary{arrows.meta} % 矢印のスタイルを指定するためのライブラリ

• \usepackage{tikz-3dplot}：3次元描画をサポートするためのライブラリ
• \usetikzlibrary{math}：tikz内で数値計算を行う際に必要なライブラリ
• \usetikzlibrary{arrows.meta}：矢印のスタイルを指定するためのライブラリ

視点の設定

3次元空間を描画する際、視点（カメラ）の位置を設定することで、図の見え方を調整できます。以下のコマンドで視点を設定します。

\tdplotsetmaincoords{60}{135}

• {60}：z軸からの仰角（上からの角度）を指定します。
• {135}：z軸周りの回転角度（水平面からの回転）を指定します。

この設定により、図が見やすい角度から表示することができます。

tikzpicture環境の設定

描画部分はtikzpicture環境内に記述します。

\begin{tikzpicture}[scale=3, tdplot_main_coords]

• scale=3：図全体のスケールを3倍に拡大する
• tdplot_main_coords：先ほど指定した視点を適用する

座標軸の描画

3次元の座標軸を描画するには、各軸に沿って線を引きます。
線を引く際は\draw (始点) -- (終点);と記述します。
線の太さ等を変更したい場合は\draw[thick]のように[]でパラメータを設定することで、線の太さ等を変更することができます。

その他の\drawのパラメータについては、新しいものが出現次第紹介していきます。

始点と終点の引数は(x座標, y座標, z座標)となっています。

% 座標軸
\draw[thick] (-0.5,0,0) -- (1.2, 0, 0);  % x軸
\draw[thick] (0,-0.5,0) -- (0, 1.2, 0);  % y軸
\draw[thick] (0,0,-0.4) -- (0, 0, 1.2);  % z軸

ここまで記述すると以下のようになります。

今回は原点スタートではなく若干長く描画したいのであえて各軸の始点を少し手前に設定しています。

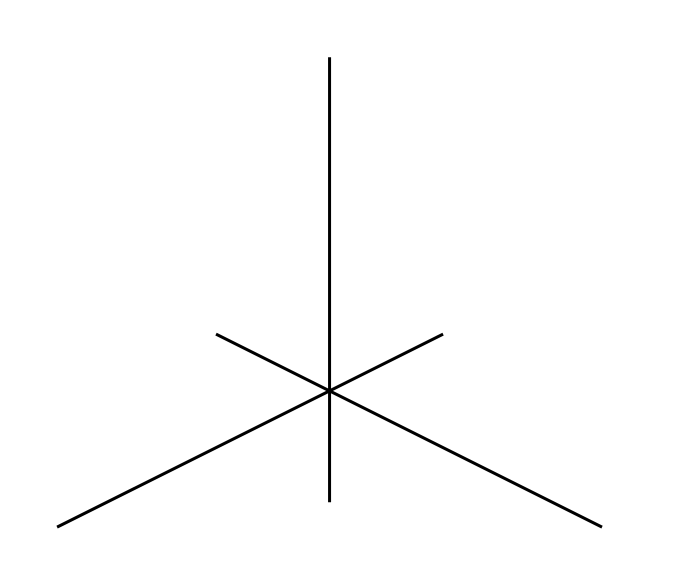
ベクトルの描画

ベクトルは原点から各方向に向かう矢印として描画します。
基本的には先ほどの座標軸の記述方法と同じです。

% ベクトルr1, r2, r3
\draw[->, ultra thick, >=Latex] (0, 0, 0) -- ({cos(20)}, {sin(20)}, 0);  % r1
\draw[->, ultra thick, >=Latex] (0, 0, 0) -- ({-sin(20)}, {cos(20)}, 0);  % r2

先ほどと違う点は、

• \drawのパラメータの中身
• 終点の引数(座標)の中身

それぞれのについて説明します。

\drawのパラメータの中身

• ->：矢印の向きを設定しています。今回は 「(始点)→(終点)」 といったように終点側に矢印の先が来るよう設定しています。
  ちなみに<->とすると両向きの矢印を描画することもできます。
• ultra thick：線の太さを設定しています。thickよりも太い線を描画することができます。またthinとすると細い線を描画することができます。
• >=Latex：これは矢印の種類を設定しています。

パラメータ	矢印の種類
latex	標準的な矢印(LaTeXスタイル)
stealth	シャープな矢印
triangle	三角形矢印
to	シンプルな矢印

終点の引数(座標)の中身

三次元空間を描画する際、具体的な座標を指定するのではなく$sin$や$cos$を使い極座標的に座標指定したい場合もあると思います。そういった場合でも対応可能です。

\draw[->, ultra thick, >=Latex] (0, 0, 0) -- ({cos(20)}, {sin(20)}, 0);

こちらのスクリプトの始点は(0,0,0)で、終点は({cos(20)}, {sin(20)}, 0)です。これは(1,0,0)を原点中心に20°だけ回転したものを表します。

cos等の三角関数を使うときはLaTeX上で計算が必要な数式として認識させる必要があるので{}を忘れないようにしましょう。

ちなみに今回は(1,0,0)を原点中心に20°だけ回転させていますが、半径が1ではないパターン（(1.5, 0, 0)のような場合）を原点中心に20°回転させる場合に関しては次のように記述してください。

\draw[->, ultra thick, >=Latex] (0, 0, 0) -- ({1.5*cos(20)}, {1.5*sin(20)}, 0);

ここまでできると以下のようになります。だいぶゴールが見えてきました。

点線の描画

次は、補助線のような点線を描画する方法を紹介します。こちらも先ほど同様基本的な線の記述方法は変わりません。

% 点線
\draw[dashed, thick, dash pattern=on 1pt off 1pt] ({cos(20)}, 0, 0) -- ({cos(20)}, {sin(20)}, 0);
\draw[dashed, thick, dash pattern=on 1pt off 1pt] (0, {sin(20)}, 0) -- ({cos(20)}, {sin(20)}, 0);
\draw[dashed, thick, dash pattern=on 1pt off 1pt] ({-sin(20)}, 0, 0) -- ({-sin(20)}, {cos(20)}, 0);
\draw[dashed, thick, dash pattern=on 1pt off 1pt] (0, {cos(20)}, 0) -- ({-sin(20)}, {cos(20)}, 0);

先ほどと変わった点は\draw[]のパラメータです。[]内でdashed`を選択しています。こちらを選択することで、点線になります。そのほかにも、破線と点線の組み合わせや二重線を指定することができます。

パラメータ	線の種類
solid	実線(デフォルト)
dotted	点線
dash dot	破線と点線の組み合わせ
dash dot dot	破線と２つの点線の組み合わせ
double	二重線

さらに線の密度を変えたい場合（点線をもっと細かくしたい場合）は、looselyやdenselyを組み合わせることができます。

例えば、loosely dashedやdensely dottedなどです。

また、dashe patternオプションを使用して、独自のパターンを定義することも可能です。今回はこちらを使用してdash pattern=on 1pt off 1ptとしていますが、これは、1pt線を引いて1pt隙間をあけるといったことを表しています。

そして、ここまでできると以下のようなグラフを描画することができます。

あともう一息です。

ラベルの追加

軸やベクトルは描画できたので、次はラベルを追加していきます。

% ラベル
\node at (1.4, 0, 0) {\textbf{$x$}};
\node at (0, 1.4, 0) {\textbf{$y$}};
\node at (0, 0, 1.4) {\textbf{$z$}};
...

ラベルは\node at (座標){ラベル内容}で描画します。
例えば、

\node at (1.4, 0, 0) {\textbf{$x$}};

であれば、(1.4, 0, 0)という座標に対して、\textbf{$x$}をプロットしています。

ラベルの位置は実際に実行しながら微調整する必要がありそうです。
1発で場所を当てるのはなかなか難しい...

ここまでくるとほぼ完成しました。

残りは回転角を表示するだけです。

回転角の描画

ベクトル間の角度を示すために弧を描画します。

% 回転角度 γ
\draw[thick] (0.3, 0, 0) arc[start angle=0, end angle=20, radius=0.3];  % arc for the angle
\node at (0.5, 0.1, 0) {$\gamma$};  

• \draw[thick] (0.3, 0, 0) arc[start angle=0, end angle=20, radius=0.3];：原点から半径0.3の弧を描画します。開始角度0度から終了角度20度までの弧を描きます。
• \node at (0.5, 0.1, 0) {$\gamma$};：弧の近くに角度を表示します。

\draw[thick](A, 0, 0)とradious=BのAとBの数値は一致させないとうまく弧を描けないようです

ついに完成

これで目的のグラフを描画することができました！！！